Bewegung von Ladungen im elektrischen Feld
Geladene Teilchen werden durch elektrische Felder abgelenkt und beschleunigt. Anwendungen der Bewegung von Ladungsträgern im elektrischen Feld sind die Braun'sche Röhre oder der Millikan-Versuch.
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Elektrische Felder beeinflussen Ladungen
- Ruhende Ladungen im elektrischen Feld
- Bewegte Ladungen im elektrischen Feld
Elektrische Felder beeinflussen Ladungen
Ein elektrisches Feld entsteht zwischen unterschiedlich geladenen elektrischen Ladungen. Es bilden sich Feldlinien, die von der positiven zur negativen Ladung zeigen. Befindet sich ein weiteres, geladenes Teilchen im elektrischen Feld, dann wird es durch das Feld beeinflusst.
Gleichnamige Ladungen ziehen sich an, ungleichnamige Ladungen stoßen sich ab. Die Ladung wird deswegen in Richtung der ungleichnamig geladenen Quelle des elektrischen Feldes gezogen.
Ruhende Ladungen im elektrischen Feld
Wenn ein geladenes Teilchen ohne Anfangsgeschwindigkeit in ein elektrisches Feld eingebracht wird, wird es in Richtung der Feldlinien beschleunigt. Es handelt sich um eine gleichmäßig beschleunigte Bewegung in Feldrichtung. Dasselbe passiert, wenn sich eine bewegte Ladung mit einer Anfangsgeschwindigkeit in Richtung der Feldlinien bewegt.
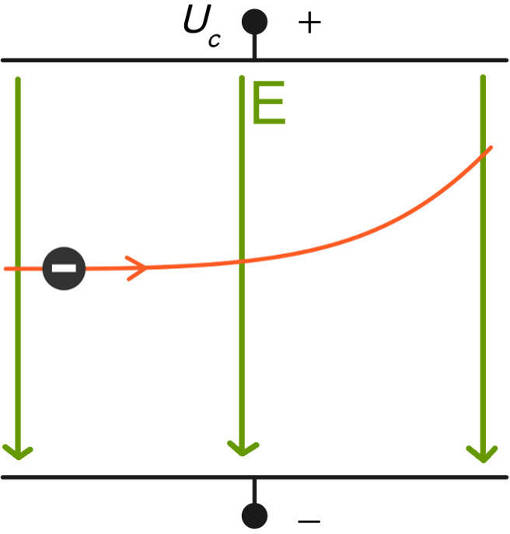
Bewegte Ladungen im elektrischen Feld
Ein geladenes Teilchen, welches sich mit einer bestimmten Anfangsgeschwindigkeit quer zu den Feldlinien eines elektrischen Feldes bewegt, wird durch die Kraft des Feldes gleichmäßig abgelenkt. Durch die abgelenkte Bewegung der Ladung entsteht eine parabelförmige Kurve.
Der Millikan-Versuch
Der Millikan-Versuch wurde 1913 von Robert Millikan vorgestellt. Er diente dazu, nachzuweisen das Ladungen in Form von diskreten Portionen auftreten und die Elementarladung $e$ genauer zu bestimmen.
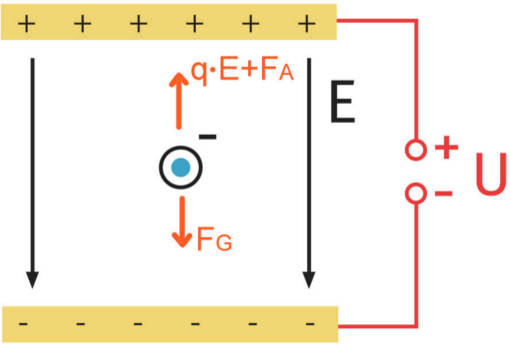
Durchführung des Millikan-Versuchs
Im ersten Schritt werden Öltröpfchen in ein elektrisches Feld eingebracht. Dieses wird so gepolt, dass die Kraft des elektrischen Feldes der nach unten wirkenden Schwerkraft des Öltropfchens entgegen wirkt. Durch Einstellung der elektrischen Feldstärke $E$ wird dafür gesorgt, dass ein Kräftegleichgewicht entsteht und ein Öltröpchen schwebt. Es kann hiermit die Ladung eines Öltropfens in Abhängigkeit von der Feldstärke, Gewichtskraft und Auftriebskraft ermittelt werden.
Im zweiten Schritt wird das elektrische Feld ausgeschaltet und die Fallgeschwindigkeit des Tröpchens gemessen. Damit kann der Radius des Öltröpchens gefunden werden. Dieser wird zur Berechnung der Gewichts- und der Auftriebskraft benötigt.
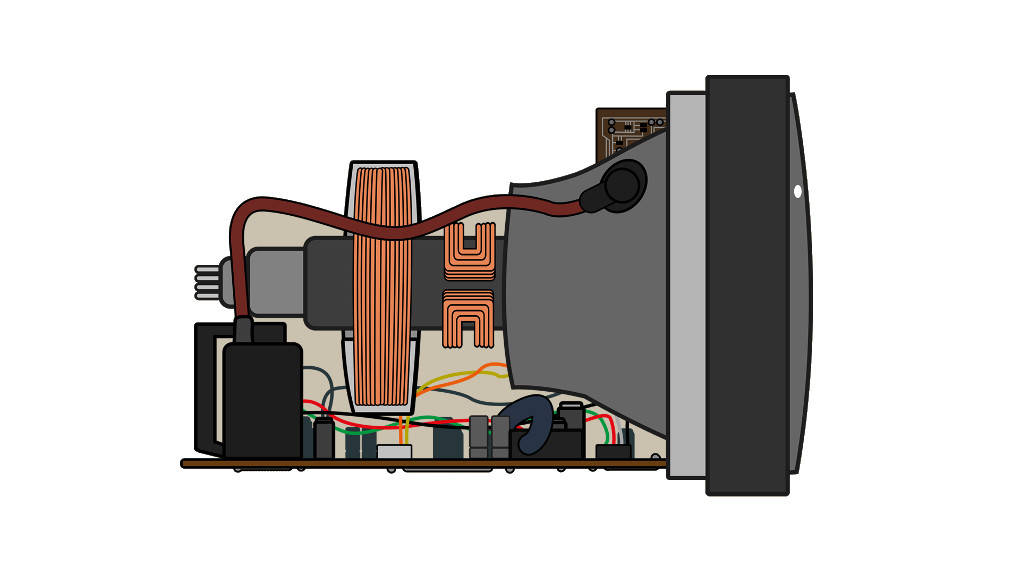
Die Braun'sche Röhre
Eine Braun'sche Röhre findest du zum Beispiel in einem alten Röhrenfernseher. Dort wird die Ablenkung von Ladungen im elektrischen Feld genutzt, um auf einem Leuchtschirm ein Bild zu erzeugen.
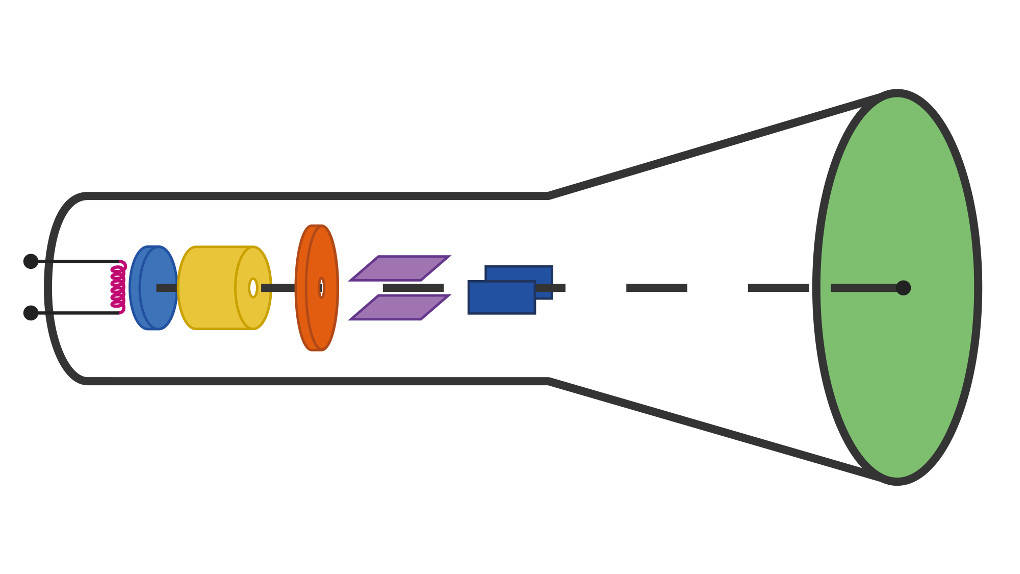
Funktion der Braun'schen Röhre
- Mithilfe des Glühelektrischen Effekts werden freie Elektronen erzeugt.
- Diese werden beschleunigt und mit einem Wehnelt-Zylinder zu einem geraden Strahl gebündelt.
- Die Elektronen werden durch zwei um 90° gedrehte elektrische Felder geschickt. Das eine lenkt sie in x-, das andere in y-Richtung ab. So können die Elektronen zu einem beliebigen Punkt auf dem Leuchtschirm gelenkt werden.
- Durch viele, schnell nacheinander auftreffende Elektronen kann ein Strahl oder sogar ein komplettes Bild erzeugt werden.
Der Faraday'sche Käfig
Der Faraday'sche Käfig ist eine aus einem leitfähigen Material bestehende und allseitig geschlossene Hülle. Diese dient der Abschirmung elektrischer Felder. Aufgrund von Influenz ist das Innere eines Faraday'schen Käfigs, der sich innerhalb eines elektrischen Feldes befindet, selbst immer feldfrei.
Dies führt dazu, dass äußere elektrische Felder keinen Einfluss auf das im Inneren befindliche haben. Aber auch elektrische Felder, die im Inneren erzeugt werden, dringen nicht nach außen. Ein Auto ist ein Faraday'scher Käfig. Deswegen passiert dir in einem Auto nichts, wenn ein Blitz einschlagen sollte.
Alle Videos und Lerntexte zum Thema
Videos und Lerntexte zum Thema
Bewegung von Ladungen im elektrischen Feld (5 Videos, 1 Lerntext)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Bewegung von Ladungen im elektrischen Feld (5 Arbeitsblätter)
Beliebteste Themen in Physik
- Temperatur
- Schallgeschwindigkeit
- Dichte
- Drehmoment
- Transistor
- Lichtgeschwindigkeit
- Elektrische Schaltungen – Übungen
- Galileo Galilei
- Rollen- Und Flaschenzüge Physik
- Radioaktivität
- Aufgaben zur Durchschnittsgeschwindigkeit
- Lorentzkraft
- Beschleunigung
- Gravitation
- Ebbe und Flut
- Hookesches Gesetz Und Federkraft
- Elektrische Stromstärke
- Elektrischer Strom Wirkung
- Reihenschaltung
- Ohmsches Gesetz
- Freier Fall
- Kernkraftwerk
- Reflexionsgesetz: Ebener Spiegel – Übungen
- Was sind Atome
- Aggregatzustände
- Infrarot, Uv-Strahlung, Infrarot Uv Unterschied
- Isotope, Nuklide, Kernkräfte
- Transformator
- Lichtjahr
- Si-Einheiten
- Fata Morgana
- Gammastrahlung, Alphastrahlung, Betastrahlung
- Kohärenz Physik
- Mechanische Arbeit
- Schall
- Elektrische Leistung
- Dichte Luft
- Ottomotor Aufbau
- Kernfusion
- Trägheitsmoment
- Heliozentrisches Weltbild
- Energieerhaltungssatz Fadenpendel
- Linsen Physik
- Ortsfaktor
- Interferenz
- Diode und Photodiode
- Wärmeströmung (Konvektion)
- Schwarzes Loch
- Frequenz Wellenlänge
- Elektrische Energie









 Bewegung von Ladungsträgern im elektrischen Feld
Bewegung von Ladungsträgern im elektrischen Feld
 Millikan-Versuch – auf der Suche nach der Elementarladung
Millikan-Versuch – auf der Suche nach der Elementarladung
 Faradayscher Käfig
Faradayscher Käfig
 Braunsche Röhre – Aufbau und Funktionsweise
Braunsche Röhre – Aufbau und Funktionsweise
 Braun'sche Röhre – Berechnung von Kenngrößen
Braun'sche Röhre – Berechnung von Kenngrößen









