Druck – Messung und Anwendung
Physikalische Grundlagen des Drucks und Schweredrucks am Beispiel des Teilchenmodells, die Abhängigkeit von anderen Zustandsgrößen sowie die Anwendung in der Hydraulik und bei Manometern
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Einleitung und physikalische Grundlagen
- Beispiel Luftdruck
- Beispiel Schweredruck
- Das Teilchenmodell
- Manometer
- Hydraulik
Einleitung und physikalische Grundlagen
Der Druck ist eine physikalische Zustandsgröße. Er beschreibt den Zusammenhang zwischen dem Betrag einer Kraft $\vec{F}$ und der Fläche $A$, auf die sie wirkt. Das Formelzeichen für den Druck ist ein kleines $p$ (vom englischen "pressure"), nicht zu verwechseln mit dem großen $P$, dem Formelzeichen für die Leistung.
$p=\frac{\vert \vec{F} \vert}{A}$
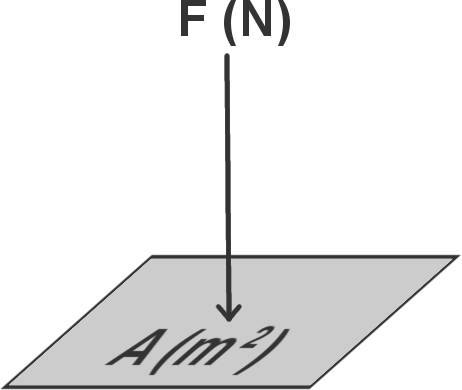
Die Einheit des Drucks ist das Pascal ($\text{Pa}$). Es beschreibt die Kraftwirkung von einem Newton auf einem Quadratmeter ($1~\frac{\text{N}}{\text{m}^2}$). Eine andere Einheit für den Druck ist $\text{bar}$. $100.000~ \text{Pa}$ entsprechen einem $\text{bar}$.
Wie das Volumen oder die Temperatur charakterisiert der Druck den Zustand eines physikalischen Systems. Solche nicht richtungsabhängigen Größen werden skalare Größen genannt. Vektorielle Größen haben neben dem Betrag zusätzlich immer eine Richtung, in die sie zeigen. Als Beispiel sei hier die Kraft $\vec{F}$ genannt.
Beispiel Luftdruck
Der Luftdruck in Meereshöhe beträgt ungefähr $1~ \text{bar}$. Also lastet auf jedem Quadratmeter der Erdoberfläche eine Kraft von $100.000~ \text{N}$. Das hört sich nach sehr viel an, aber unsere Körper sind von jeher an diesen Druck angepasst, so dass wir nichts davon merken. In einem abgeschlossenen System, beispielsweise in einem Autoreifen, ist der Luftdruck überall gleich groß.
Beispiel Schweredruck
Sicher ist dir schon einmal aufgefallen, dass du einen Druck auf den Ohren spürst, wenn du tief ins Wasser tauchst. Der Grund ist, dass das Wasser aufgrund seiner Masse eine Gewichtskraft auf dein Trommelfell ausübt. Unter Wasser herrscht also ebenfalls Druck, man spricht von Schweredruck. Die Formel für den Schweredruck lautet:
$p=\rho g h$.
Dabei ist $\rho=\frac{m}{V}$ die Dichte, $g$ die Erdbeschleunigung und $h$ die Höhe der Wassersäule über dir.
Das Teilchenmodell
Das Teilchenmodell dient dazu, sich eine Vorstellung davon zu machen, was Druck eigentlich ist. Als Beispiel soll ein aufgeblasener Luftballon betrachtet werden: Im Teilchenmodell werden die kleinsten Bausteine der Luft als Kugeln beschrieben, die sich im Ballon frei bewegen können. Dabei stoßen sie sich untereinander an oder prallen gegen die Ballonwand. Dabei findet ein Impulsübertrag bzw. eine Kraftwirkung von den Teilchen auf die Wand statt. Das Verhältnis der gesamten ausgeübten Kraft und der Oberfläche des Ballons ist der Druck.
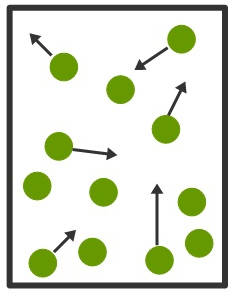
Der Druck in eingeschlossenen Gasen, wie im Ballon, hängt auch von der Temperatur ab. Die Temperatur eines Gases ist die mittlere Bewegungsenergie der Teilchen. Erhöht sich die Temperatur, so werden auch die Teilchen schneller und stoßen häufiger. Folglich steigt der Druck. Verringst du stattdessen die Gasmenge, indem du Luft entweichen lässt, so verringert sich auch der Druck, da es weniger Teilchen gibt, die stoßen können. Ebenso ist das Volumen entscheidend. Drückst du den Ballon zusammen, verkleinerst du sein Volumen. Dabei kannst du spüren, wie der Druck steigt, bis der Ballon platzt.
Manometer
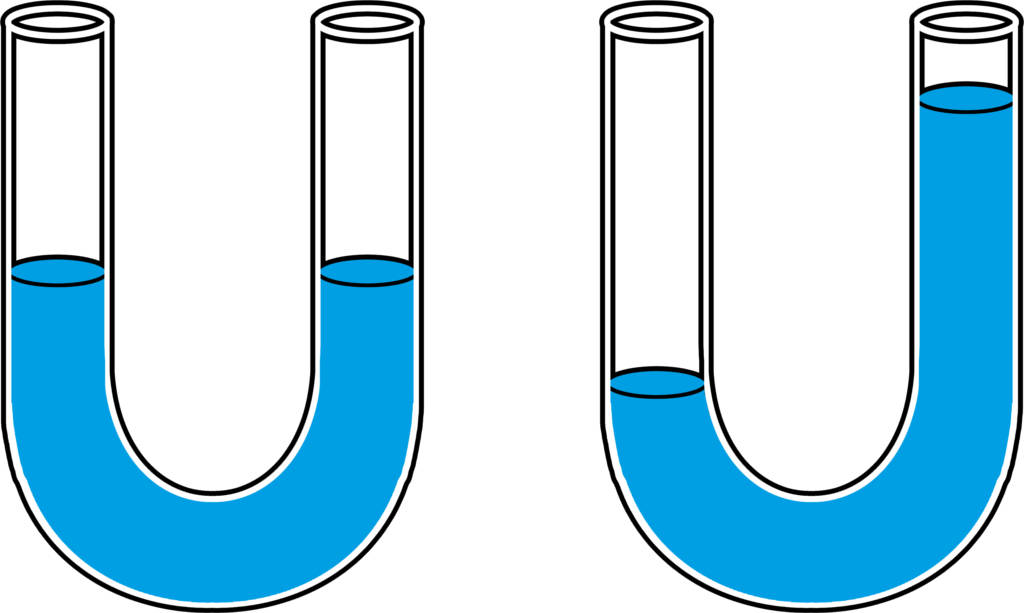
Ein Manometer ist ein Messgerät zum Messen des Drucks. Wird es speziell zum Messen des Luftdrucks verwendet, so bezeichnet man es als Barometer. Ein Dosenbarometer verformt sich je nach äußerem Druck. Die Ausbeulung der Dose wird auf einen Zeiger übertragen, der den Luftdruck auf einer Skala anzeigt. Eine andere Form des Barometers ist das Flüssigkeitsbarometer. Dabei handelt es sich um ein gebogenes Röhrchen, das auf einer Seite offen und auf der anderen luftdicht verschlossen ist. Je nach Luftdruck ändert die Flüssigkeit seine Füllhöhe.
Die genaue Kenntnis des Luftdrucks dient Flugzeugen zur Bestimmung der Flughöhe. In der Meteorologie wird er zur Wettervorhersage benötigt.
Hydraulik
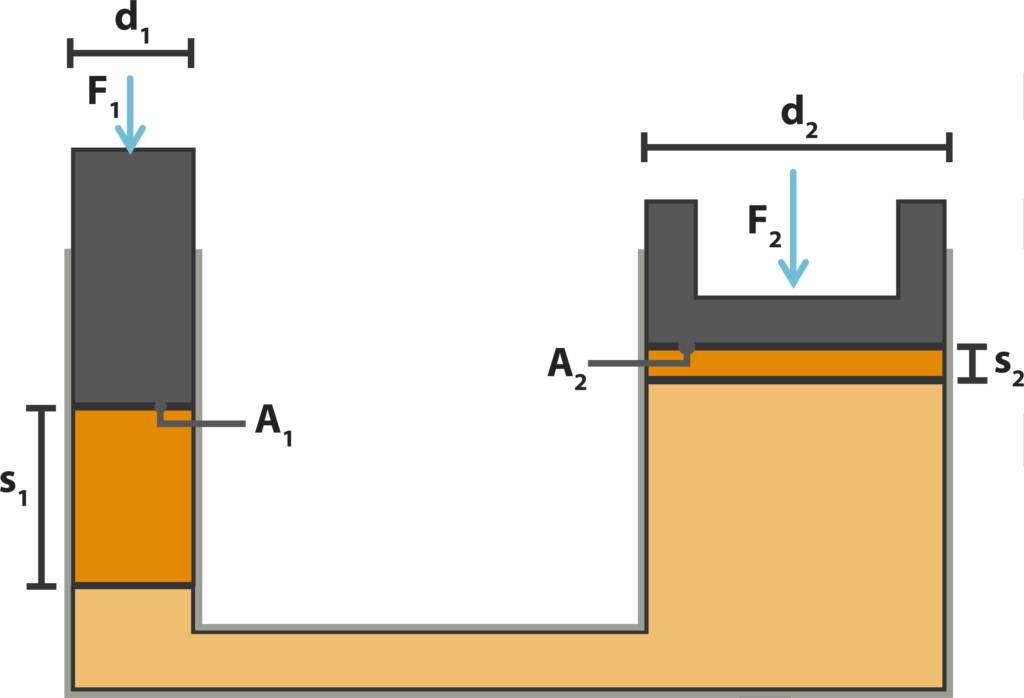
Die Tatsache, dass der Druck in einem System überall gleich groß ist, wird in der Hydraulik als Kraftwandler genutzt. So ist es möglich, ein tonnenschweres Auto mit bloßer Muskelkraft anzuheben. Alles was du dafür benötigst ist ein Wagenheber. Die Muskelkraft wird über den einen Hebel auf eine relativ kleine Fläche übertragen. Dadurch entsteht überall in der Hydraulikleitung ein gleich großer Druck. Auf der anderen Seite des Wagenhebers wirkt der Druck auf eine viel größere Fläche, dadurch erhöht sich auch die Kraft in gleicher Weise. Ist das Verhältnis der Flächen richtig gewählt, kann die eigene Muskelkraft so sehr verstärkt werden, dass sie ausreicht, einen Wagen anzuheben.
Alle Videos und Lerntexte zum Thema
Videos und Lerntexte zum Thema
Druck – Messung und Anwendung (7 Videos, 3 Lerntexte)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Druck – Messung und Anwendung (8 Arbeitsblätter)
-
 Druck im Alltag
PDF anzeigen
Druck im Alltag
PDF anzeigen -
 Druck – Was ist Druck?
PDF anzeigen
Druck – Was ist Druck?
PDF anzeigen -
 Druck – im Teilchenmodell
PDF anzeigen
Druck – im Teilchenmodell
PDF anzeigen -
 Druck – Hydrostatisches Paradoxon
PDF anzeigen
Druck – Hydrostatisches Paradoxon
PDF anzeigen -
 Luftdruck – Aufbau und Funktion eines Barometers
PDF anzeigen
Luftdruck – Aufbau und Funktion eines Barometers
PDF anzeigen -
 Druck in eingeschlossenen Gasen
PDF anzeigen
Druck in eingeschlossenen Gasen
PDF anzeigen -
 Sachaufgaben zum Schweredruck in Gasen
PDF anzeigen
Sachaufgaben zum Schweredruck in Gasen
PDF anzeigen -
 Hydraulik
PDF anzeigen
Hydraulik
PDF anzeigen
Beliebteste Themen in Physik
- Temperatur
- Schallgeschwindigkeit
- Dichte
- Drehmoment
- Transistor
- Lichtgeschwindigkeit
- Elektrische Schaltungen – Übungen
- Galileo Galilei
- Rollen- Und Flaschenzüge Physik
- Radioaktivität
- Aufgaben zur Durchschnittsgeschwindigkeit
- Lorentzkraft
- Beschleunigung
- Gravitation
- Ebbe und Flut
- Hookesches Gesetz Und Federkraft
- Elektrische Stromstärke
- Elektrischer Strom Wirkung
- Reihenschaltung
- Ohmsches Gesetz
- Freier Fall
- Kernkraftwerk
- Reflexionsgesetz: Ebener Spiegel – Übungen
- Was sind Atome
- Aggregatzustände
- Infrarot, Uv-Strahlung, Infrarot Uv Unterschied
- Isotope, Nuklide, Kernkräfte
- Transformator
- Lichtjahr
- Si-Einheiten
- Fata Morgana
- Gammastrahlung, Alphastrahlung, Betastrahlung
- Kohärenz Physik
- Mechanische Arbeit
- Schall
- Elektrische Leistung
- Dichte Luft
- Ottomotor Aufbau
- Kernfusion
- Trägheitsmoment
- Heliozentrisches Weltbild
- Energieerhaltungssatz Fadenpendel
- Linsen Physik
- Ortsfaktor
- Interferenz
- Diode und Photodiode
- Wärmeströmung (Konvektion)
- Schwarzes Loch
- Frequenz Wellenlänge
- Elektrische Energie





















