Elektromagnetische Schwingungen und ihre Eigenschaften

Inhaltsverzeichnis zum Thema

• Schwingungen des elektromagnetischen Schwingkreises
• Die Thomson'sche Schwingungsgleichung - Eigenfrequenz des Schwingkreises
• Gedämpfter elektromagnetischer Schwingkreis
• Erzwungene Schwingung und Resonanz
• Resonanz
• Phasenverschiebung

Schwingungen des elektromagnetischen Schwingkreises

Du hast in einem anderem Thementext bereits kennengelernt, was ein elektromagnetischer Schwingkreis ist und wie er aufgebaut ist. Sicher erinnerst du dich, dass ein elektromagnetischer Schwingkreis periodische Schwingungen ausführt, die sich mit mechanischen Schwingungen wie dem Faden- oder Federpendel vergleichen lassen. Die Schwingungsdauer eines elektromagnetischen Schwingkreises hängt dabei im einfachsten Fall nur von der Kapazität des Kondensators und der Induktivität der Spule ab.

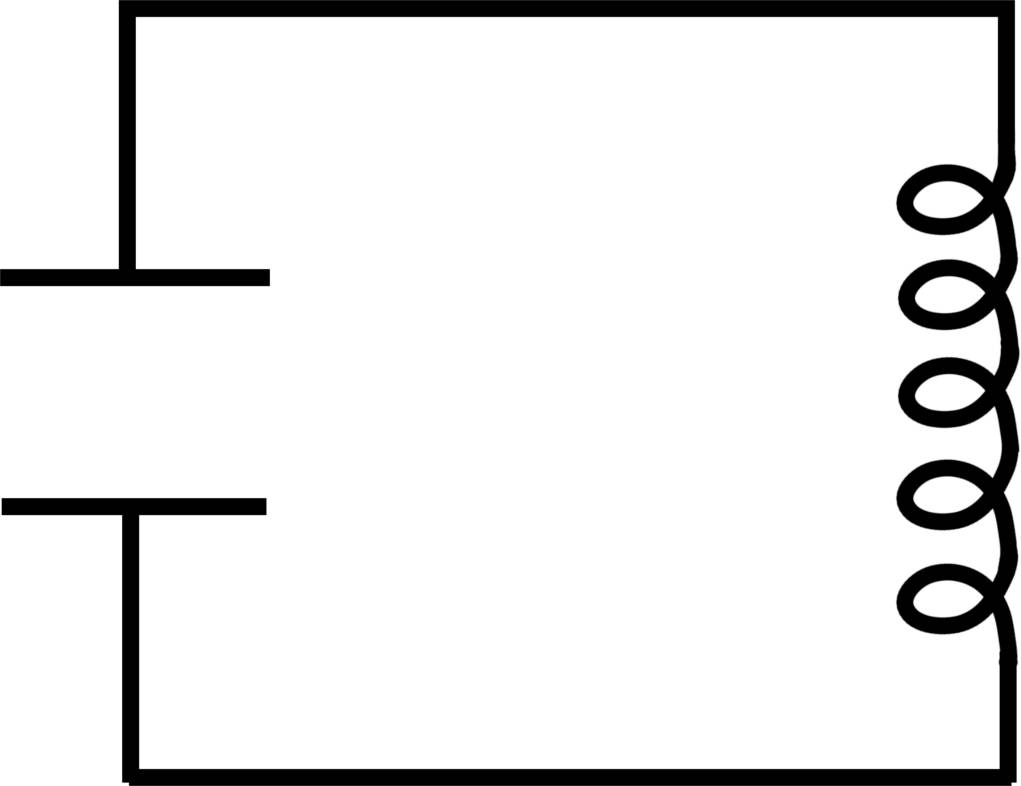
Die Thomson'sche Schwingungsgleichung - Eigenfrequenz des Schwingkreises

In einem idealen elektromagnetischen Schwingkreis haben weder die Kabel noch die Bauteile elektrische Widerstände. Das heißt, dass der Schwingkreis keine Energie durch Wärmeentwicklung an ohmschen Widerständen verliert. In diesem Fall spricht man von einer harmonischen oder ungedämpften Schwingung.

Die im Kondensator gespeicherte elektrische Energie und die magnetische Energie in der Spule variieren mit der Zeit, die Summe ist allerdings konstant.

$ E_{el} + E_{mag} = \dfrac12 CU^2 + \dfrac12 LI^2 = const. $

Die Spannung $U$ eines Kondensators lässt sich durch $U=\frac{Q}{C}$ ausdrücken. Der Strom $I$ in der Spule ist gegeben durch die Ableitung der Ladung $I=\dot{Q}$. Zunächst kannst du diese beiden Größen in der obigen Gleichung ersetzten und selbige anschließend ableiten. Die Ableitung ist anschaulich gesprochen die zeitliche Änderung der Energiesumme. Da diese konstant ist, ihre zeitliche Änderung also Null ist, ist auch das Ergebnis der Ableitung Null.

$ \dot{Q}(L\ddot{Q}+\dfrac1{C}Q)=0 $

Du weißt bereits, dass die elektromagnetische Schwingung des Schwingkreises ein periodischer Vorgang ist, er sich also nach der Periodendauer $T$ wiederholt. Die obige Differentialgleichung lässt sich demnach lösen, indem du die Ladung $Q$ durch eine periodische Funktion wie den Kosinus $Q(t)=Q_0\cos{(\omega t + \varphi)}$ beschreibst. Eingesetzt in den Ausdruck in der Klammer ergibt sich die Thomson'sche Schwingungsgleichung.

$\omega=\dfrac1{\sqrt{LC}} \text{ bzw. } T=2\pi\sqrt{LC}$

Hier zeigt sich erneut die Analogie zu mechanischen Oszillatoren wie dem Feder- und Fadenpendel, denn deren Schwingungsgleichungen sind von derselben mathematischen Form und liefern ähnliche Ergebnisse für die Schwingungsdauer:

$T_{Feder}=2\pi\sqrt{\dfrac{k}{m}} \text{ und } T_{Faden}=2\pi\sqrt{\dfrac{l}{g}}$.

Gedämpfter elektromagnetischer Schwingkreis

Im Falle eines realen elektromagnetischen Schwingkreises haben die Bauteile und Kabel ohmsche Widerstände $R$. Diese erwärmen sich, wenn Strom fließt. Aufgrund der Wärmeentwicklung geht Energie aus dem Schwingkreis ($E_R$) verloren, sodass die Amplitude sinkt.

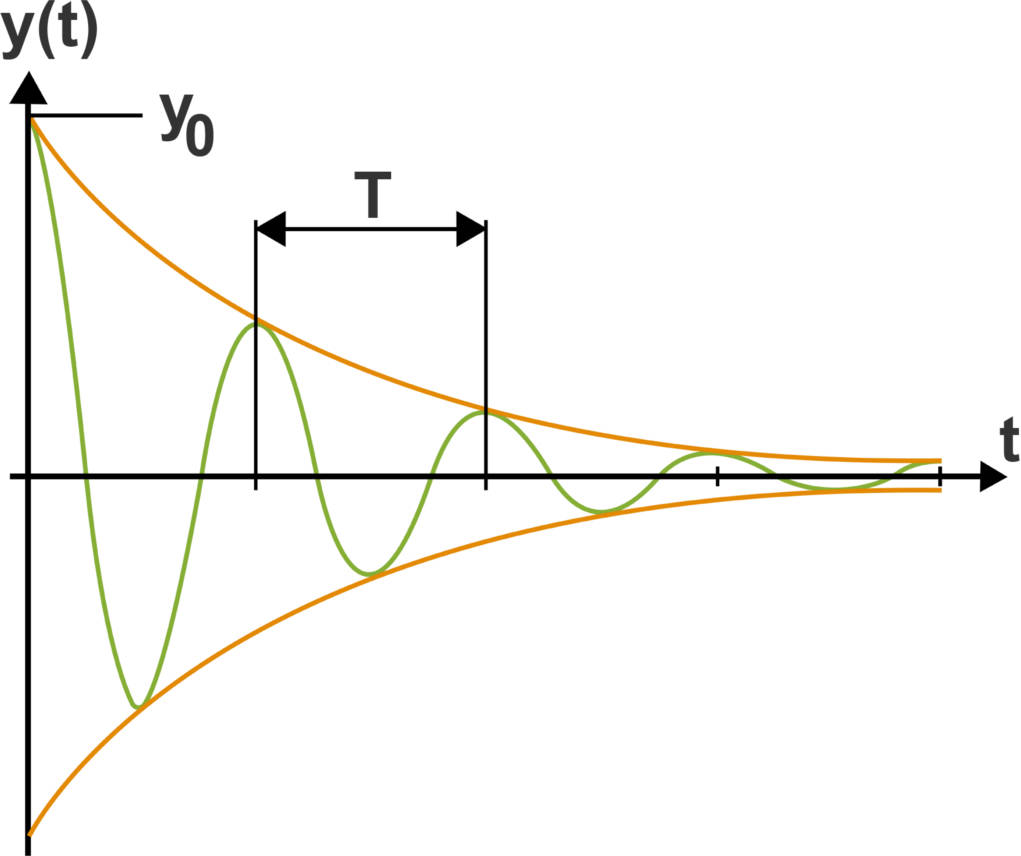
Die Summe aus elektrischer und magnetischer Energie im Schwingkreis sowie verloren gegangener Energie ist natürlich trotzdem konstant.

$ E_{el} + E_{mag} + E_R = const. $

Die mathematische Herleitung der Schwingungsgleichung im gedämpften Fall ist etwas komplizierter, weswegen hier darauf verzichtet wird. Als Eigenfrequenz $\omega$ ergibt sich

$ \omega=\sqrt{\dfrac1{LC}-\dfrac{R^2}{4L^2}}$.

Wie du siehst, erhältst du die Gleichung des harmonischen Oszillators, wenn du $R=0\,\Omega$ einsetzt.

Erzwungene Schwingung und Resonanz

Für jede Schwingung lässt sich eine Eigenfrequenz $\omega$ bestimmen. Oben wurde beispielsweise gezeigt, was die Eigenfrequenz des elektromagnetischen Schwingkreises ist. Die Eigenfrequenz ist die Frequenz, in der das System schwingt, wenn es sich selbst überlassen wird. Dies nennt man auch Eigenschwingung.

Ein schwingendes System kann aber auch durch eine äußere periodische Kraft angeregt werden. Die Schwingfrequenz des Systems wird sich dann der Frequenz der äußeren Kraft angleichen. Man spricht von erzwungener Schwingung.

Du kannst beispielsweise ein Fadenpendel in deiner Hand schwingen lassen. Wenn du nun aber deine Hand gleichmäßig vor- und zurückbewegst, passt sich die Schwingfrequenz des Pendels irgendwann deiner Hand an. Beim elektromagnetischen Schwingkreis könnte diese Aufgabe ein Wechselstromgenerator erfüllen.

Resonanz

Sollte der Fall eintreten, dass die äußere anregende Frequenz der Eigenfrequenz des Systems entspricht, so vergrößert sich die Amplitude. Ein anschauliches Beispiel ist das Anschubsen beim Schaukeln. Das Anschubsen entspricht hier der äußeren, anregenden Kraft. Gibst du genau im richtigen Moment Schwung (mit gleicher Frequenz in der die Schaukel schwingt), so schaukelst du immer höher (die Amplitude wird größer). Man spricht von Resonanz.

Eine Resonanz kann auch gefährlich sein. Eine Resonanzkatastrophe tritt beispielsweise ein, wenn eine Brücke oder ein Hochhaus im Wind zusammenbricht. Die Resonanz kann aber auch positiv sein. Im Falle des elektromagnetischen Schwingkreises findet sie im Radio Anwendung.

Phasenverschiebung

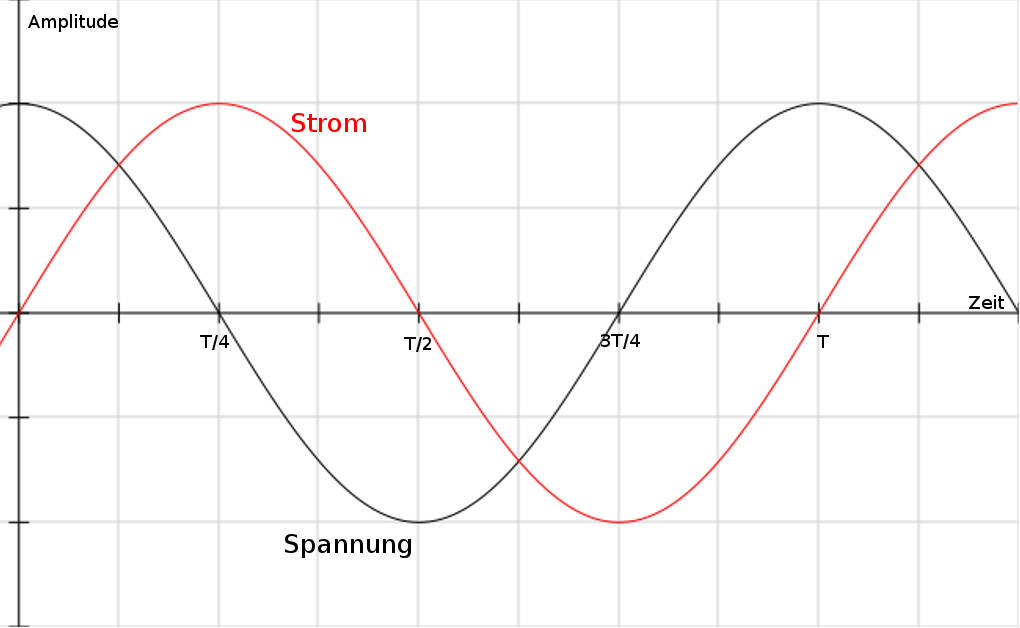
Eine Phasenverschiebung zwischen zwei Schwingungen ist gegeben, wenn die Systeme zwar mit gleicher Frequenz $\omega$ schwingen, ihre Maxima aber zu unterschiedlichen Zeitpunkten erreichen. Betrachtest du die Spannung und den Strom in einem elektromagnetischen Schwingkreis genauer, stellst du fest, dass sich beide Größen durch eine Sinusfunktion beschreiben lassen. Die Zeit, in der sich die Spannung im Kondensator ab- und wieder aufbaut ist gleich groß wie die Zeit, in der die Stromstärke auf ihr Maximum ansteigt und wieder Null wird: Die Frequenz ist identisch. Allerdings erreicht der Strom seinen Maximalwert erst in dem Moment, da die Spannung Null ist. Strom und Spannung sind also um eine viertel Periode phasenverschoben.