Zufallsvariable und Erwartungswert

Inhaltsverzeichnis zum Thema

• Was ist eine Zufallsvariable?
  • Diskrete Zufallsgrößen
  • Stetige Zufallsgrößen
• Zusammenhang Zufallsvariable und Wahrscheinlichkeitsverteilung
• Beispiel Wahrscheinlichkeitsverteilung einer diskreten Zufallsvariable: Binomialverteilung
• Was ist der Erwartungswert?
  • Das Glücksrad
• Der Erwartungswert bei Spielen
  • Ein faires Spiel?
  • Wann ist ein Spiel fair?
• Der Erwartungswert bei binomialverteilten Zufallsgrößen

Was ist eine Zufallsvariable?

Eine Zufallsvariable oder auch Zufallsgröße ist eine Zuordnung, die jedem möglichen Ergebnis eines Zufallsversuches eine Zahl zuordnet. Die Werte, welche die Zufallsgröße annehmen kann, werden Realisierungen dieser Zufallsgröße genannt.

• Dies kann das Ergebnis selbst sein, wie zum Beispiel die Augenzahl $1$ bis $6$ beim Würfelwurf.
• Beim Werfen einer Münze kann dem Ergebnis „Kopf“ die Zahl $1$ und dem Ergebnis „Zahl“ die Zahl $0$ zugeordnet werden.

Eine Zufallsvariable wird mit einem Großbuchstaben $X$ oder $Y$ oder $Z$ bezeichnet. Du unterscheidest zwischen diskreten und stetigen Zufallsgrößen.

Diskrete Zufallsgrößen

Betrachte das Zufallsexperiment Werfen eines Würfels.Die Zufallsgröße kann die Werte $1; 2; 3; 4; 5; 6$ annehmen. Dies sind $6$, also endlich viele, Werte.

Diskrete Zufallsgrößen können nur eine endliche oder abzählbar unendliche Menge an Werten annehmen.

Was bedeutet eigentlich „abzählbar unendlich viele“? Wenn du die Sterne am Himmel betrachtest, kannst du diese zählen. Da du jedoch nicht zu einem Ende kommst, spricht der Mathematiker hier von abzählbar unendlich vielen Menschen.

Stetige Zufallsgrößen

Du stehst morgens an der Bushaltestelle und beobachtest die Zeit, zu welcher der Bus ankommt. Diese Zeit wird in einem gewissen Intervall liegen. Hier kann die Zufallsgröße überabzählbar unendlich viele Werte annehmen, da du das Intervall beliebig klein aufteilen.

Stetige Zufallsgrößen können im Gegensatz zu diskreten Zufallsgrößen innerhalb eines beliebigen Intervalls überabzählbar unendlich viele Werte annehmen.

Zusammenhang Zufallsvariable und Wahrscheinlichkeitsverteilung

Eine Wahrscheinlichkeitsverteilung ( kurz Verteilung) gibt an, wie sich die Wahrscheinlichkeiten auf die möglichen Werte einer Zufallsvariablen verteilen.

Diese Definition kannst du dir an dem Beispiel des Werfens eines Würfels klarmachen:

• Die Zufallsgröße kann die Werte $1; 2; 3; 4; 5$ und $6$ annehmen. Dies ist gerade die oben liegende Augenzahl.
• Die Wahrscheinlichkeit für das Eintreten einer bestimmten Augenzahl ist immer gleich. Diese beträgt $\frac16$.
• Damit ist $P(X=1)=...=P(X=6)=\frac16$.

Übrigens: Zufallsexperimente, in denen jedes Ergebnis mit der gleichen Wahrscheinlichkeit eintritt, werden Laplace-Experimente genannt. Die resultierende Verteilung ist die Gleichverteilung.

Beispiel Wahrscheinlichkeitsverteilung einer diskreten Zufallsvariable: Binomialverteilung

Abschließend siehst du ein Beispiel zur Binomialverteilung. Dies ist eine Wahrscheinlichkeitsverteilung einer diskreten Zufallsvariable.

Du wirfst eine Münze $10$-mal. Die Ergebnisse dieses Zufallsexperimentes sind $10$-Tupel, in denen „$K$“ für „Kopf“ und „$Z$“ für „Zahl“ vorkommen. Die Zufallsgröße $X$ ordne jedem dieser Ergebnisse die Anzahl zu, wie oft „$K$“ vorkommt. Diese Zufallsgröße ist binomialverteilt.

Zum Beispiel könnte das Ergebnis lauten $(K|K|K|K|Z|K|Z|K|Z|Z)$. Du siehst, in diesem Ergebnis kommt $6$-mal „$K$“ vor. Es ist also $X=6$. Es gibt mehrere solcher $10$-Tupel, in denen $6$-mal „$K$“ vorkommt. Wie viele dies sind kannst du mithilfe der Kombinatorik bestimmen. Zur Berechnung wird der Binomialkoeffizient verwendet:

$\begin{pmatrix} n\\ k \end{pmatrix}$

Insbesondere kannst du nun die Wahrscheinlichkeit der Zufallsvariable $X$ bestimmen, welche den Wert $6$ annimmt. Dies schreibst du so: $P(X=6)$

Hierfür verwendest du die Formel nach Bernoulli:

$P(X=k)=B_{n;p}(k)=\begin{pmatrix} n\\ k \end{pmatrix}\cdot p^k\cdot (1-p)^{n-k}$.

Darin kommen die folgenden Größen vor:

• $n$ ist die Länge der Bernoullikette, also die Anzahl der Durchführungen des Zufallsexperimentes. Hier ist $n=10$.
• $k$ ist die Anzahl der Treffer oder auch Erfolge, also hier $k=6$ für $6$-mal „$K$“.
• $p$ ist die Trefferwahrscheinlichkeit oder auch Erfolgswahrscheinlichkeit. Diese ist in dem betrachteten Beispiel mit dem Münzwurf $p=0,5$.
• Die Gegenwahrscheinlichkeit der Erfolgswahrscheinlichkeit ist $1-p$, die Misserfolgswahrscheinlichkeit. Diese ist hier ebenfalls $0,5$.

Nun kannst du die Wahrscheinlichkeit berechnen:

$P(X=6)=B_{10;0,5}(6)=\begin{pmatrix} 10\\ 6 \end{pmatrix}\cdot 0,5^6\cdot 0,5^{10-6}=\frac{105}{512}\approx0,2051$.

Ebenso kannst du Wahrscheinlichkeiten $P(X=k)$ für $k=0;~1;~2;...;~10$ berechnen.

Was ist der Erwartungswert?

Um zu verstehen, was ein Erwartungswert ist, wäre ist hilfreich, wenn du dich schon ein bisschen mit der folgenden Schreibweise auskennst. Wir betrachten ein Zufallsexperiment mit der Ergebnismenge

$\Omega=\{e_1,e_2,\dots,e_n\}$

und den Wahrscheinlichkeiten $p_i=P(e_i)$ für $i=1,\dots,n$.

Zusätzlich sei die Zufallsvariable oder auch Zufallsgröße $X$ gegeben, welche jedem Ergebnis der Ergebnismenge eine Zahl zuordnet:

$X:\begin{array}{lcr} \Omega&\rightarrow&\mathbb{R}\\ e_i&\rightarrow&x_i \end{array}$

Der Erwartungswert $E(X)$ (oder auch $\mu$) dieser Zufallsgröße ist wie folgt definiert:

$E(X)=\mu=\sum\limits_{i=1}^nx_i\cdot P(X=x_i)$.

Dabei sind $x_1$, ..., $x_n$ die möglichen Ausprägungen der Zufallsgröße und $P(X=x_i)=P(e_i)$ ist die Wahrscheinlichkeit für das Eintreten der Ausprägung $x_i$.

Genau wie das arithmetische Mittel ist der Erwartungswert ein Lageparameter.

Das Glücksrad

Dieses Glücksrad wird einmal gedreht. (Hinweis: Glücksräder machen nicht glücklich.)

Die Zufallsgröße $X$ ordnet den ungeraden Zahlen $1$, $3$, $5$ die Zahl $10$ und den geraden $2$, $4$ die Zahl $20$ zu.

$P(X=10)=P( \{ 1,3,5 \} )=\frac35$

$P(X=20)=P( \{ 2,4 \} )=\frac25$

Damit kann der Erwartungswert berechnet werden:

$E(X)=\mu=\frac35\cdot 10+\frac25\cdot 20=6+8=14$.

Du wirst vielleicht sagen: „$14$?! Das ergibt doch keinen Sinn!“ Der Wert $14$ ergibt tatsächlich erst Sinn, wenn wir das Zufallsexperiment sehr häufig durchführen. Dann werden wir im Schnitt eine $14$ gedreht haben.

Der Erwartungswert bei Spielen

Ein faires Spiel?

Paul hat sich auf folgendes Spiel eingelassen: Er setzt $2~€$ und darf das Glücksrad einmal drehen. Es kommt zu den folgenden Auszahlungen:

• Bei einem roten Feld erhält er $1~€$,
• bei einem grünen Feld $1,50~€$
• und bei einem blauen Feld $4~€$.

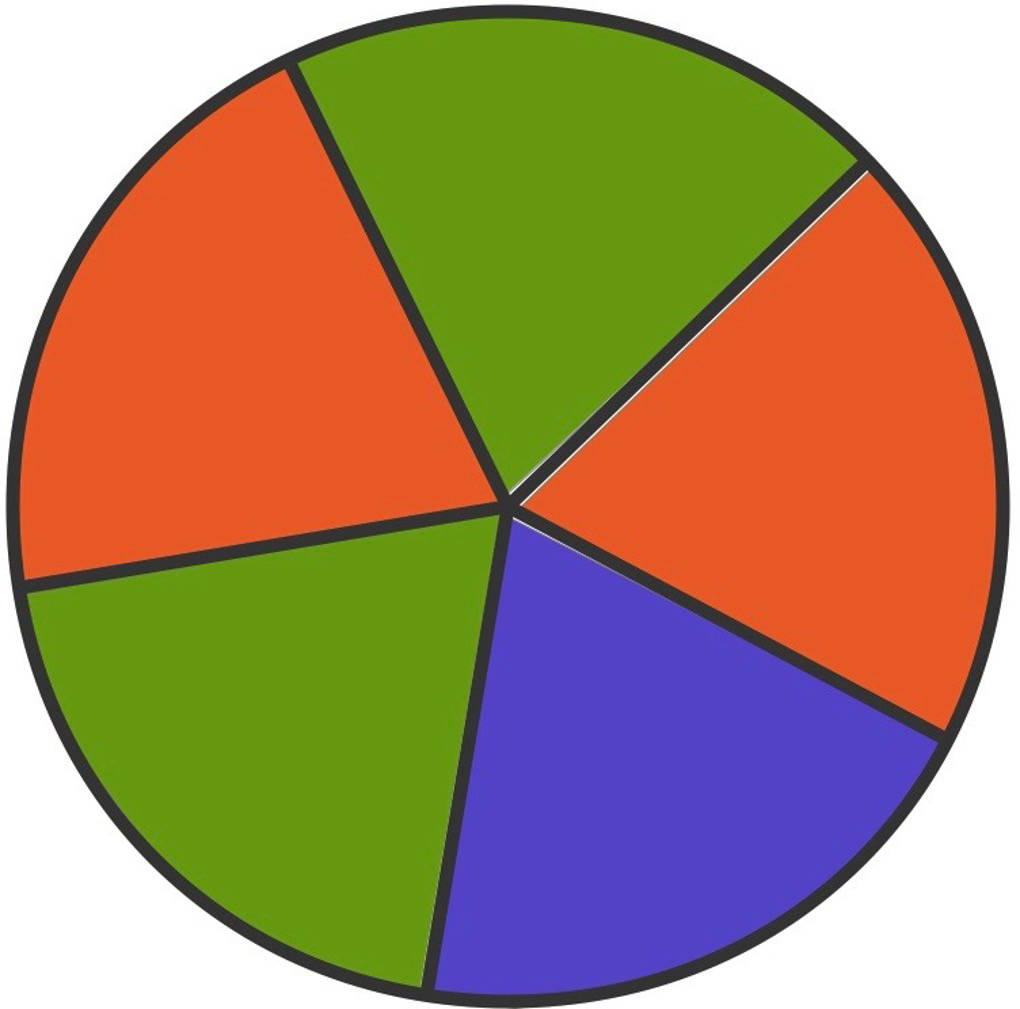
Nun fragt sich Paul: Ist dieses Spiel auf lange Sicht fair?

Aber was versteht man unter einem fairen Spiel? Ein Spiel heißt fair, wenn es auf lange Sicht sowohl für den Spieler als auch für den Anbieter des Spiels gleich ausgeht. Sowohl der Anbieter als auch der Spieler verliert weder auf lange Sicht, noch gewinnt einer von beiden.

Schauen wir uns die Bedingungen genauer an:

• Die Ergebnismenge ist $\Omega=\{$rot, grün, blau$\}$.
• Die Wahrscheinlichkeiten der Ergebnisse sind $P($rot$)=P($grün$)=\frac25$ und $P($blau$)=\frac15$.

Zunächst schauen wir uns die Zufallsgröße $X$ an.

$X:\begin{array}{lcr} \text{ rot}&\rightarrow&1,00~€\\ \text{grün}&\rightarrow&1,50~€\\ \text{blau}&\rightarrow&4,00~€ \end{array}$

Nun kannst du den Erwartungswert berechnen.

$E(X)=\frac25\cdot 1~€+\frac25\cdot 1,50~€+\frac15\cdot 4~€=1,80~€$

Weil Paul pro Spiel $2~€$ Einsatz bezahlen muss und er im Schnitt weniger (nämlich $1,80~€$) gewinnt, ist dieses Spiel für ihn nicht fair.

Wann ist ein Spiel fair?

Nun kann man sich natürlich auch fragen, welche Auszahlung $x$ in Euro Paul für das blaue Feld erhalten sollte, damit das Spiel fair ist.

Es muss dann gelten $E(X)=2~€$. Dies führt zu der folgenden Gleichung:

$E(X)=\frac25\cdot 1~€+\frac25\cdot 1,50~€+\frac15\cdot x~€=2~€$.

Diese Gleichung ist äquivalent zu

$1~€+\frac15\cdot x~€=2~€$.

Nun kannst du auf beiden Seiten $1~€$ subtrahieren und dann mit $5$ multiplizieren. Dies führt zu $x=5$.

Also müsste Paul eine Auszahlung von $5~€$ für „blau“ erhalten, damit das Spiel fair ist.

Der Erwartungswert bei binomialverteilten Zufallsgrößen

Eine Münze soll 12-mal geworfen werden.

$X$ sei die Zufallsgröße für die Häufigkeit des Auftretens von „Kopf“. Hier liegt eine Binomialverteilung vor. Der Erwartungswert einer binomialverteilten Zufallsgröße lässt sich wie folgt berechnen:

$E(X)=\mu=n\cdot p=12\cdot \frac12=6$.

Dabei ist $n$ die Länge der Bernoullikette. Die Länge der Bernoullikette sagt aus, wie oft das Experiment durchgeführt wird. Die Wahrscheinlichkeit für das Eintreten von „Kopf“ wird durch $p$ beschrieben.

Bei $12$ Würfen kommt also durchschnittlich $6$ Mal „Kopf“. Wir können auch sagen: Bei $12$ Würfen erwarten wir $6$ Mal „Kopf“. Das ist doch logisch, oder?