Rekonstruktion ganzrationaler Funktionen – Rutsche


in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
Grundlagen zum Thema Rekonstruktion ganzrationaler Funktionen – Rutsche
In diesem Video beschäftigen wir uns mit der Rekonstruktion ganzrationaler Funktionen, indem wir uns ein ganz konkretes Beispiel anschauen: Es soll der Funktionsgraph einer Wasserrutsche bestimmt werden. Nach einer kurzen, theoretischen Wiederholung der Lösungsstrategie werden wir gemeinsam die Aufgabe Schritt für Schritt lösen, indem wir die nötigen Bedingungen für die Rekonstruktion ganzrationaler Funktionen formulieren. Viel Spaß!
Rekonstruktion ganzrationaler Funktionen – Rutsche Übung
-
Nenne die Bedingungen für eine Funktion dritten Grades.
TippsEine Funktion n-ten Grades benötigt immer n+1 Bedingungen.
Lokale Maxima und Minima erkennt man daran, dass an den Extremstellen die Ableitung Null ist.
Der Hoch- und Tiefpunkt sind mit ihren Koordinaten angegeben. Das bedeutet, dass wir durch Einsetzen der x-Werte in die Funktion die y-Werte erhalten müssen.
LösungWelche Schlüsse sich aus den Angaben ziehen lassen, kann man hier sehr gut erkennen.
Der Hoch- und Tiefpunkt sind mit ihren Koordinaten angegeben. Das bedeutet, dass wir durch Einsetzen der x-Werte in die Funktion die y-Werte erhalten müssen.
Für die Punkte $(0|5)$ und $(5|0)$ ergeben sich folgende Bedingungen:
- $f(0)=5$
- $f(5)=0$
An jeder Stelle, die eine Extremstelle ist, muss die erste Ableitung Null sein. Da wir unsere Extrema kennen, erhalten wir als weitere Bedingungen:
- $f'(0)=0$
- $f'(5)=0$
-
Bestimme die fehlenden Parameter der Funktion.
TippsDu musst das folgende Gleichungssystem lösen:
$\begin{array}{cccccc} 125a&+25b&+5c&+d&=&0 \\ 75a&+10b&+c&&=&0 \end{array}$
LösungAusgangspunkt ist die allgemeine Form der Funktion $f$ und ihrer Ableitung $f'$:
$f(x)=a\cdot x^3 + b\cdot x^2 + c\cdot x + d$
$f'(x)=3\cdot a\cdot x^2 + 2\cdot b \cdot x + c$
Gehen wir die Bedingungen der Reihe nach durch:
Die erste Bedingung $f(0)=5$ liefert:
$f(0)= a\cdot 0^3 + b\cdot 0^2 + c\cdot 0 + d=5$
Übrig bleibt $d=5$. Somit haben wir schon einen Parameter.
Die zweite Bedingung besagt, dass $f(5)=0$ gilt:
$f(5)=a\cdot 5^3 + b\cdot 5^2 + c\cdot 5 + d=0$
Daraus ergibt sich:
$125a + 25b + 5c + d = 0$
Die dritte Bedingung $f'(0)=0$ liefert
$f'(0)=3a \cdot 0^2 + 2b\cdot 0 + c=0$
Übrig bleibt $c=0$, unser nächster Parameter.
Die vierte Bedingung besagt, dass $f'(5)=0$ gilt:
$f'(5)=3\cdot a\cdot 5^2 + 2\cdot b \cdot 5 + c$
Wir erhalten:
$75a+10b+c=0$
Wir haben also zwei Parameter direkt gefunden und noch zwei Bedingungen in Gleichungsform. Aus diesen beiden bilden wir nun folgendes Gleichungssystem:
$\begin{array}{cccccc} 125a&+25b&+5c&+d&=&0 \\ 75a&+10b&+c&&=&0 \end{array}$
Wir setzen nun die Werte für $c$ und $d$ ein, die wir bereits kennen. Danach sieht das Gleichungssystem so aus:
$\begin{array}{ccccc} 125a&+25b&+5&=&0 \\ 75a&+10b&&=&0 \end{array}$
Dieses kannst du nun auf beliebige Art und Weise lösen (zum Beispiel durch Einsetzen einer Zeile in die andere).
Am Ende erhältst du folgende Ergebnisse:
$a=0,08$ und $b=-0,6$
Die Funktion sieht schließlich so aus:
$f(x)=0,08x^3 - 0,6x^2 + 5$
-
Arbeite die Bedingungen aus den Informationen über $f$ heraus.
TippsBei Extremstellen der Funktion besitzt der Ableitungsgraph eine Nullstelle.
Man erhält die y-Koordinate, wenn man die x-Koordinate in die Funktionsgleichung einsetzt.
LösungZu jedem der zwei Extrempunkte können wir jeweils zwei Bedingungen aufstellen.
Beginnen wir mit dem Hochpunkt bei $(-1|3)$.
Hier erhält man die y-Koordinate, wenn man die x-Koordinate in die Funktionsgleichung einsetzt:
- $f(-1)=3$
- $f'(-1)=0$
- $f(6)=-2$
- $f'(6)=0$
-
Bilde die Funktionsgleichung von $f$.
TippsZwei Parameter müssen Null sein.
Für Extremstellen muss notwendigerweise $f'(x_E)=0$ gelten.
Bei Wendestellen heißt die Bedingung $f''(x_W)=0$.
LösungBilden wir zunächst die ersten drei Ableitungen:
$f(x)=a\cdot x^3 + b\cdot x^2 + c\cdot x + d$
$f'(x)=3\cdot a\cdot x^2 + 2\cdot b\cdot x + c$
$f''(x)=6\cdot a\cdot x + 2\cdot b$
Nun sehen wir uns unsere Bedingungen an und wie wir sie formulieren können:
- Der Wendepunkt im Ursprung liefert $f(0)=0$ und $f''(0)=0$.
- Die Nullstelle $x=1$ gibt uns die zusätzliche Bedingung $f(1)=0$.
- Der Wert für Parameter $a$ ist gegeben: $a=3$
$f(0)=a\cdot 0^3 + b\cdot 0^2 + c\cdot 0 + d$
Damit diese Gleichung $0$ wird, muss gelten: $d=0$
Betrachten wir nun die Bedingung für den Wendepunkt und seine Bestimmung: Hier muss auch die zweite Ableitung Null ergeben.
$f''(0)=6\cdot a\cdot 0 + 2 \cdot b$
Damit diese Gleichung Null wird, muss $b=0$ sein. Damit haben wir gezeigt, dass die Parameter $b$ und $d$ wegfallen und somit auch ihre kompletten Summanden in der Funktionsgleichung:
$f(x)=a\cdot x^3 + c\cdot x$
Den Wert für $a$ kennen wir bereits:
$f(x)=3 \cdot x^3 + c\cdot x$
Nun sollen wir mit Hilfe der positiven Nullstelle ($x=1$) den letzten Parameter bestimmen. Es muss $f(1)=0$ gelten.
$\begin{align} 3\cdot 1^3 + c\cdot 1&=0 \\ 3 + c &= 0 &|& -3\\ c&=-3 \end{align}$
Somit lautet die gesuchte Funktionsgleichung:
$f(x)=3x^3-3x$
-
Gib die nötige Anzahl von Bedingungen an.
TippsFür eine Funktion n-ten Grades sind n+1 Bedingungen nötig, um sie zu rekonstruieren.
LösungHierfür gibt es einen Merksatz, den du dir merken oder besser aufschreiben solltest:
Wenn du eine Funktion n-ten Grades rekonstruieren willst, brauchst du dafür n+1 Bedingungen.
Das bedeutet für unser Beispiel:
Wir haben eine Funktion dritten Grades. Deshalb brauchen wir $3+1=4$ Bedingungen, um sie rekonstruieren zu können.
-
Ermittle die gesuchten Parameter der Funktionsgleichung.
TippsJeder Punkt kann als eine Bedingung angesehen werden - du erhältst ein Gleichungssystem mit vier Zeilen und vier Variablen.
Dein umgeformtes Gleichungsystem könnte so aussehen:
Dein umgeformtes Gleichungsystem könnte so aussehen:
LösungHier muss man mit keiner Ableitung rechnen, da nur vier verschiedene Punkte bekannt sind, von denen man nicht weiß, ob es sich um Extrem- oder Wendepunkte handelt.
Betrachten wir eine Funktion dritten Grades $f(x)=a\cdot x^3 + b\cdot x^2 + c\cdot x + d$, so können wir alle Punkte als Bedingungen verwenden. Das sieht dann für die Punkte $A, B, C$ und $D$ so aus:
$a\cdot 1^3 + b\cdot 1^2 + c\cdot 1 +d = 4$
$a\cdot 2^3 + b\cdot 2^2 + c\cdot 2 +d = 2$
$a\cdot 4^3 + b\cdot 4^2 + c\cdot 4 +d = 4$
$a\cdot 5^3 + b\cdot 5^2 + c\cdot 5 +d = 20$
Das können wir in ein Gleichungssystem schreiben:
$\begin{array}{c|cccccc|} I & a & +b & +c & +d &=& 4 \\ II & 8a & +4b & +2c & +d &=& 2 \\ III & 64a & +16b & +4c & +d &=& 4 \\ IV & 125a & +25b & +5c & +d &=& 20 \end{array}$
Nun eliminieren wir nacheinander aus verschiedenen Zeilen verschiedene Variablen. Zuerst eliminieren wir alle $d$ in den Zeilen $II, III$ und $IV$. Dazu addieren wir zu jeder dieser Zeilen das negative der ersten Zeile $(+ I\cdot (-1))$. Danach sieht das Gleichungssystem so aus:
$\begin{array}{c|cccccc|} I & a & +b & +c & +d &=& 4 \\ II & 7a & +3b & +c & &=& -2 \\ III & 63a & +15b & +3c & &=& 0 \\ IV & 124a & +24b & +4c & &=& 16 \end{array}$
Als nächstes eliminieren wir die $c$ aus den Zeilen $III$ und $IV$. Dazu rechnen wir $III + II\cdot (-3)$ bzw. $IV + II\cdot (-4)$. Danach sollte dein Gleichungssystem diese Form haben:
$\begin{array}{c|cccccc|} I & a & +b & +c & +d &=& 4 \\ II & 7a & +3b & +c & &=& -2 \\ III & 42a & +6b & & &=& 6 \\ IV & 96a & +12b & & &=& 24 \end{array}$
Nun müssen wir nur noch das $b$ aus der letzten Zeile eliminieren, um eine Dreiecksgestalt zu erhalten. Dazu addieren wir folgendes: $IV + III\cdot (-2)$. Nun sieht es so aus:
$\begin{array}{c|cccccc|} I & a & +b & +c & +d &=& 4 \\ II & 7a & +3b & +c & &=& -2 \\ III & 42a & +6b & & &=& 6 \\ IV & 12a & & & &=& 12 \end{array}$
Jetzt kann man das Gleichungssystem von unten nach oben auflösen:
$IV:$
$12a = 12$ liefert $a=1$.
Wert für $a$ in $III$ einsetzen:
$42\cdot 1 +6b = 6$ liefert $b=-6$.
Werte für $a$ und $b$ in $II$ einsetzen:
$7\cdot 1 +3\cdot (-6)+c=-2$ liefert $c=9$.
Werte für $a$, $b$ und $c$ in $I$ einsetzen:
$1 - 6 + 9 + d = 4$ liefert $d=0$.
Damit lautet die gesuchte Funktionsgleichung:
$f(x)=x^3 - 6x^2 + 9x$
9.859
sofaheld-Level
6.600
vorgefertigte
Vokabeln
8.306
Lernvideos
38.657
Übungen
33.694
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Klassenstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung




 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?











@Yoon Sojina:
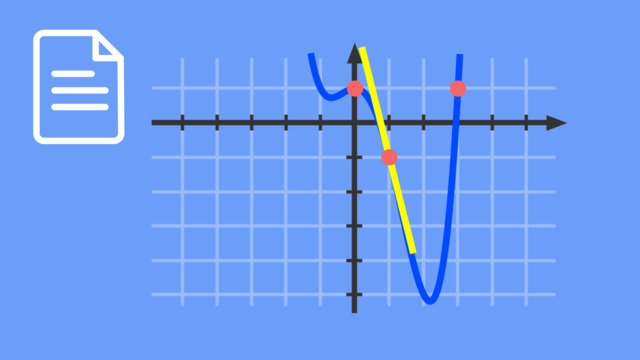
Eine Funktion mit Grad 4 hat bis zu 3 lokale Extremwerte. Zum Beispiel wenn du für aufsteigende x erst ein Minimum, dann ein Maximum und dann noch ein Minimum bekommst.
Wenn du dann eine Gleichungssystem finden willst, brauchst du sogar 5 Bedingungen.
woher erkennt man, dass die Funktion der Rutsche hat 4 Grad besitzt?
@Ajenth S.: Eine lineare Gleichung ist eine Gleichung ersten Grades. Die Variable, bspw. x, kommt hierbei mit keiner höheren Potenz als 1 vor. Ein LGS ist also ein System aus mehreren linearen Gleichungen.
Da es sich hierbei um eine Funktion 3. Grades handelt, entsteht hier eben kein lineares Gleichungssystem.
Ich hoffe ich konnte deine Frage beantworten.
Heißt es nicht LGS also Lineares Gleichungssystem?