Wurfbewegungen

Inhaltsverzeichnis zum Thema

• Physikalische und mathematische Grundlagen
  • Kräfte und Reibung
  • Gleichmäßig beschleunigte oder gleichförmige Bewegung
  • Superposition
• Der senkrechte Wurf
• Der waagerechte Wurf
• Der schiefe Wurf
  • Wurfbewegungen im Sport

Physikalische und mathematische Grundlagen

Die Newton'sche Mechanik (klassische Mechanik) beschäftigt sich mit dem Verhalten von Körpern, auf die eine Kraft wirkt. Dazu zählen auch Wurfbewegungen.

Kräfte und Reibung

In der klassischen Mechanik musst du dir immer im Klaren darüber sein, welche Kräfte wirken und wohin sie zeigen. Wirfst du einen Ball, so wirkt die Kraft deiner Arme, um den Ball in eine gewisse Richtung zu beschleunigen. Diese Kraft wird aber in der Regel nicht beachtet. Sie wird dadurch umgangen, dass man dem Ball stattdessen eine gewisse (Anfangs-)Geschwindigkeit $v_0$ zuweist, die er in dem Moment hat, in dem er deine Hand verlässt. Da diese Anfangsgeschwindigkeit eine klare Richtung besitzt stellt man sie auch so dar:

$\vec{v_0}$.

Während des Fluges ist der Ball dem Luftwiderstand ausgesetzt. Die Widerstandskraft wird allerdings oft vernachlässigt. Die einzige verbleibende Kraft, die während des Fluges eines Balls wirkt, ist die Gravitationskraft (Erdanziehungskraft) $F_{G}=mg$. Sie zeigt stets in Richtung Erde.

Gleichmäßig beschleunigte oder gleichförmige Bewegung

Nach Newtons 2. Axiom ruft eine Kraft immer eine Beschleunigung hervor. In Richtung Erde ist eine Bewegung aufgrund der Gravitation also stets beschleunigt. Da die Erdanziehungskraft sich nicht ändert, ist die Beschleunigung gleichmäßig und es gilt das Weg-Zeit-Gesetz

$s(t)=s_0+v_0 t + \frac12 a t^2$.

Nach Newtons 1. Axiom verbleibt ein Körper in seinem Bewegungszustand, sofern keine Kraft wirkt. Dies ist der Fall für eine Bewegung parallel zur Erdoberfläche. Eine solche Bewegung ist gleichförmig und es gilt das Weg-Zeit-Gesetz

$s(t)=s_0+v_0 t$.

Durch einmaliges Ableiten nach der Zeit erhältst du die Geschwindigkeit $v(t)=\dot{s(t)}$ und durch zweimaliges Ableiten die Beschleunigung $a(t)=\dot{v(t)}=\ddot{s(t)}$.

Superposition

Wie du siehst, gibt es einen Unterschied, ob eine Bewegung senkrecht oder parallel zur Erdoberfläche ausgeführt wird. Das Superpositionsprinzip besagt aber, dass sich Bewegungen, die sich gegenseitig nicht beeinflussen, ungestört überlagern. Bei einem schiefen Wurf, dessen Flugbahn zu einem bestimmten Teil sowohl parallel als auch senkrecht zur Erdoberfläche verläuft, kannst du folglich problemlos beide Teilbewegungen einzeln betrachten. Das erleichtert die mathematische Betrachtung, da du vektorielle Größen wie die Geschwindigkeit in Anteile parallel und senkrecht zur Erde aufteilen kannst.

Der senkrechte Wurf

Bei einem senkrechten Wurf nach oben musst du das Superpositionsprinzip noch nicht beachten, da die Flugbahn des Balls ausschließlich senkrecht zur Erdoberfläche ist und damit in die gleiche Richtung wie die Gravitation zeigt (y-Richtung). Wirfst du einen Ball von der Höhe $s_0$ aus mit der Geschwindigkeit $+v_0$ nach oben, so lautet das Weg-Zeit-Gesetz

$s(t)=s_0+v_0 t - \frac12 g t^2$

und das Geschwindigkeit-Zeit-Gesetz

$v(t)= +v_0 - g t$.

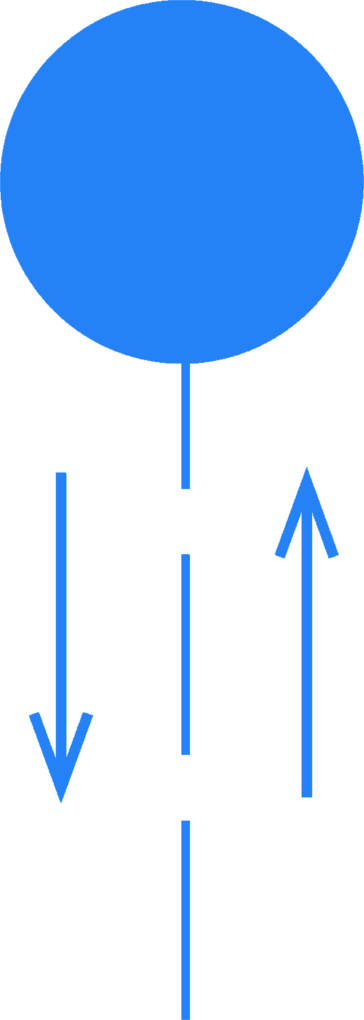
Bei einem Wurf ist die allgemeine Beschleunigung $a$ mit der Erdbeschleunigung $g$ gleichzusetzen. Das Minus im letzten Term muss da stehen, da die Gravitationskraft nach unten zeigt, der Ball aber nach oben geworfen wird. Daraus folgt unweigerlich, dass die Geschwindigkeit nach einer bestimmten Zeit $t$ gleich Null wird. Am sogenannten Umkehrpunkt steht der Ball für einen kurzen Moment bewegungslos in der Luft. Dies ist auch der Grund, warum Passagiere bei einem Parabelflug im Umkehrpunkt kurz schwerelos sind. Anschließend wird die Geschwindigkeit negativ, was dem Herunterfallen des Balls entspricht (eine negative Geschwindigkeit bedeutet im mathematischen Sinne eine Bewegung entgegen der Richtung der Achse).

Bei einem senkrechten Wurf nach unten ändert sich lediglich das Vorzeichen der Anfangsgeschwindigkeit. Lässt du den Ball einfach los ($v_0=0$) erhältst du die Gleichungen für einen freien Fall. Die obigen Gleichungen kannst du je nach gegebener Größe umstellen.

Der waagerechte Wurf

Beim waagerechten Wurf kannst du das Superpositionsprinzip benutzen. Der Ball wird nach einer bestimmten Zeit auf der Erden aufschlagen. Den Fall des Balls in y-Richtung (nach unten), kannst du unabhängig von der Bewegung nach rechts (x-Richtung) betrachten und es gelten dieselben Formeln wie beim freien Fall (senkrechter Wurf ohne Anfangsgeschwindigkeit in y-Richtung). Du kannst dich davon überzeugen, wenn du zwei Kugeln von einem Tisch herunterfallen lässt. Unter der Voraussetzung, dass beide gleichzeitig von der Kante fallen, spielt es keine Rolle, wie unterschiedlich schnell die Kugeln gerollt sind: Sie werden immer gleichzeitig den Boden berühren.

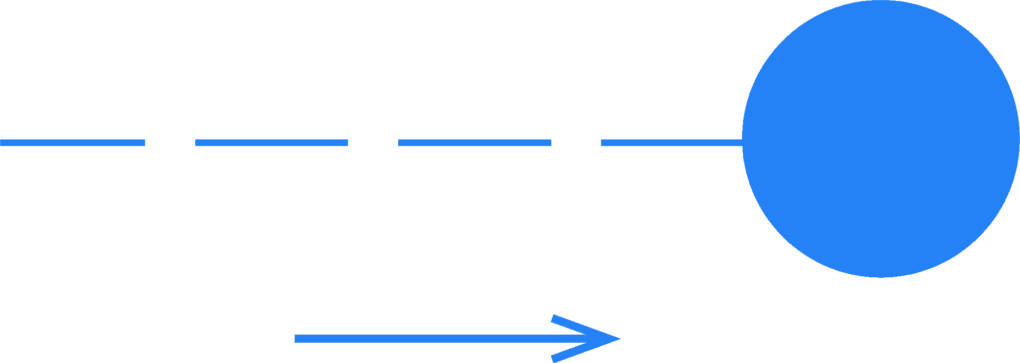
Der Ball hat beim Verlassen deiner Hand eine Anfangsgeschwindigkeit in x-Richtung. Die Bewegung in x-Richtung ist kräftefrei (Gravitation wirk nur nach unten). Es gelten daher die Gesetze zur gleichförmigen Bewegung.

Der schiefe Wurf

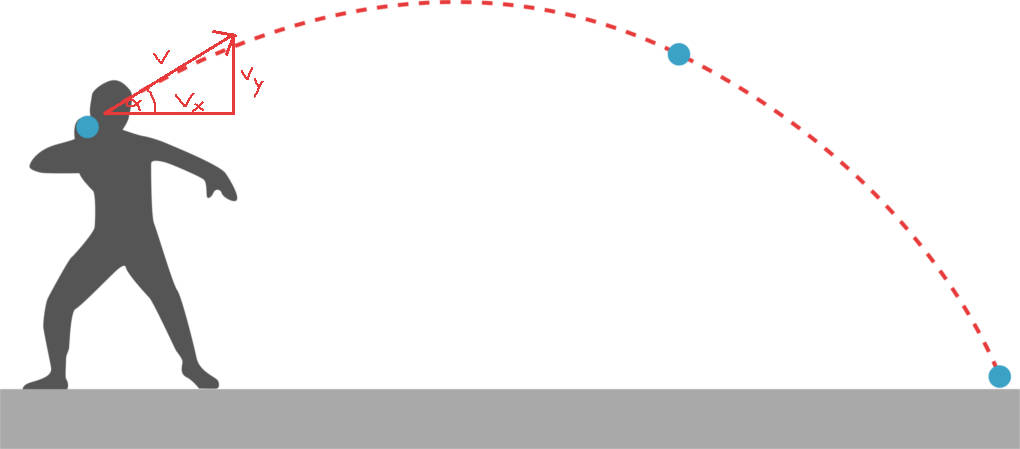
Der schiefe Wurf kombiniert den senkrechten und den waagerechten Wurf. Die Besonderheit hier ist, dass die Anfangsgeschwindigkeit weder ausschließlich nach unten oder zur Seite gerichtet ist, sondern eben in einem bestimmten Winkel $\alpha$ schief. Die Geschwindigkeit $v$ ist eine vektorielle Größe und als solche lässt sie sich in einen Anteil parallel zur Erde $v_x$ und senkrecht zur Erde $v_y$ aufteilen. Mit der Trigonometrie ergibt sich

$v_x=v \cos{(\alpha)} \text{ und } v_y=v \sin{(\alpha)}$.

Die tatsächliche Geschwindigkeit ist mit dem Satz des Pythagoras

$v=\sqrt{v_x^2+v_y^2}$.

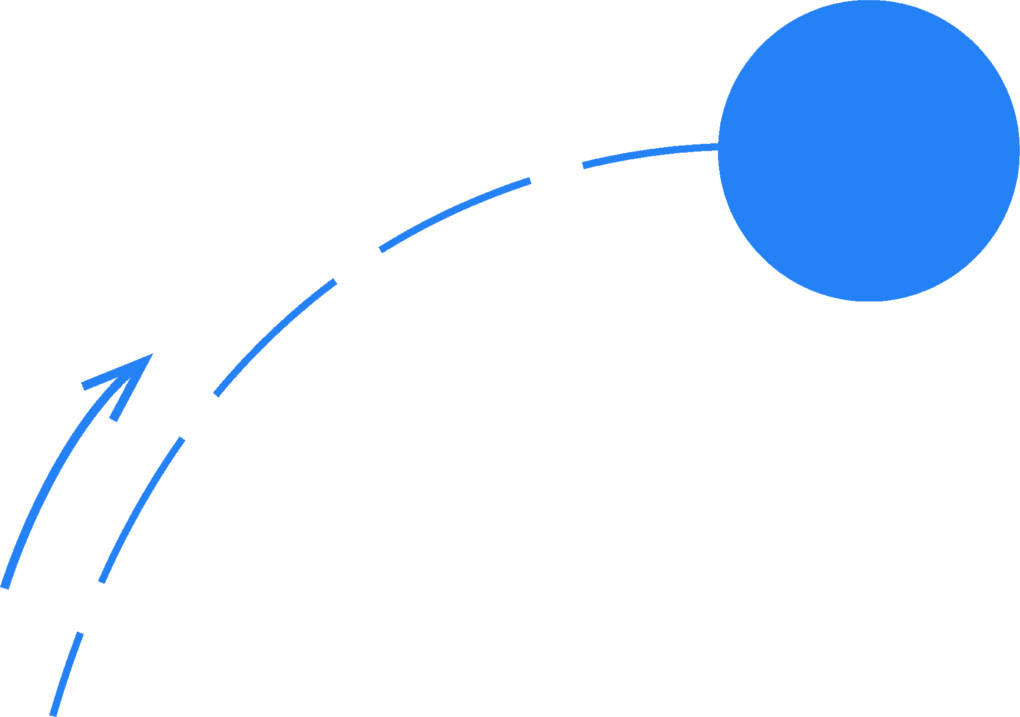
Die Flugbahn des Balls beschreibt eine Parabel und hat als solche einen Umkehrpunkt wie der senkrechte Wurf. Ebenso wird eine Entfernung zur Seite zurückgelegt, wie beim waagrechten Wurf. Wie weit ein Ball fliegt, hängt vom Winkel ab, mit dem er geworfen wird.

Wurfbewegungen im Sport

Willst du bei den nächsten Bundesjugendspielen mit dem Ball so weit wie möglich kommen, solltest du im Winkel von $45^\circ$ werfen. Auch beim Weitsprung gelten die Regeln des schiefen Wurfes.