Translationsbewegungen, Trägheit und Bezugssystem
Differentielle Betrachtung der Translation und Abhängigkeit vom Inertialsystem, Galilei-Transformation sowie Scheinkräfte und Trägheit
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Geschwindigkeit und Beschleunigung - klassische und differentielle Beschreibung
- Relativitätsprinzip - die Abhängigkeit vom Bezugssystem
- Inertialsysteme
Geschwindigkeit und Beschleunigung - klassische und differentielle Beschreibung
Aus der Schule kennst du bereits das Weg-Zeit-Gesetz, das den Zusammenhang zwischen der zurückgelegten Strecke $s(t)$ und der Geschwindigkeit $v$, Beschleunigung $a$ und Zeit $t$ angibt. Es lautet:
$ s(t)=\frac12 a t^2+v_0 t+s_0 $ .
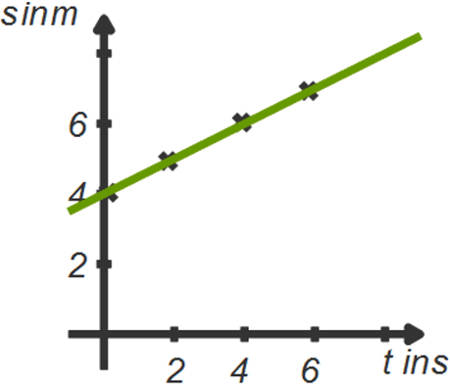
Diese Formel entspricht dem Weg-Zeit-Gesetz einer gleichmäßig beschleunigten Bewegung, also einer Bewegung mit konstanter Beschleunigung wie etwa einem freien Fall. Diese Formel enthält aber auch das Weg-Zeit-Gesetz für eine gleichförmige Bewegung mit konstanter Beschleunigung. Du erhältst es, wenn du die die Beschleunigung gleich Null setzt ($a=0$). Für eine solche gleichförmige Bewegung ist das Weg-Zeit-Diagramm eine Gerade durch den Anfangspunkt $s_0$. Die Geschwindigkeit ist dann einfach die Steigung der Geraden.
Für die gleichmäßig beschleunigte Bewegung ($a\neq0$), deren Gesetzmäßigkeiten mit der Attwood'sche Fallmaschine studiert wurden, ist das Weg-Zeit-Diagramm eine Parabel.
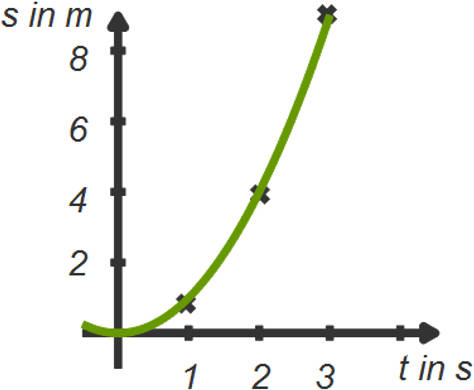
Du weißt, dass die Geschwindigkeit in diesem Fall nicht konstant ist. Die Momentangeschwindigkeit an einem bestimmten Ort ist dann die Steigung der Tangente an diesem Punkt. Wie du aus dem Mathematikunterricht weißt, entspricht dies gerade der Ableitung an diesem Punkt. Tatsächlich ist das bekannte Geschwindigkeit-Zeit-Gesetz
$ v(t)=a t + v_0$
die Ableitung der obigen Formel für das Weg-Zeit-Gesetz nach der Zeit. Die Beschleunigung wiederum ist die Ableitung der Geschwindigkeit. Differentiell ausgedrückt ist also:
$ v(t)=\frac{\text{d}s}{\text{d}t} \text{ und } a(t)=\frac{\text{d}v}{\text{d}t}=\frac{\text{d}^2 s}{\text{d}t^2}. $
Die bekannten Weg-Zeit- und Geschwindigkeit-Zeit-Gesetze gelten nur für eine konstante Geschwindigkeit bzw. eine konstante Beschleunigung. Mit dem differentiellen Gesetz kannst du nun auch die in der Realität häufigeren Fälle berechnen, für die die Konstanz von Geschwindigkeit bzw. Beschleunigung nicht gilt. Dies trifft zum Beispiel bereits auf jede reale Autofahrt zu.
Relativitätsprinzip - die Abhängigkeit vom Bezugssystem
Der Ort eines Objekts und auch dessen Geschwindigkeit wird jedem Beobachter anders vorkommen. Stelle dir zwei Beobachter vor, die in einem Park auf zwei Bänken sitzen, die zehn Meter voneinander entfernt sind. Läuft nun ein Jogger vorbei und beide Beobachter sollten nach einer gewissen Zeit angeben, wie weit der Jogger entfernt ist, so würden sich deren Antworten um zehn Meter unterscheiden. Dieses Beispiel zeigt, dass der Ort eines Objekts nicht absolut ist, sondern von der Position des Beobachters abhängt. In der Physik spricht man von verschiedenen Bezugssystemen und dem Relativitätsprinzip.

Obwohl die beiden Beobachter bei der Angabe des Ortes des Joggers verschiedener Meinung sind, so sind sie sich bei dessen Geschwindigkeit einig. Vergleichst du das Weg-Zeit- und das Geschwindigkeit-Zeit-Gesetz von oben, stellst du fest, dass der Anfangsort $s_0$ wegfällt und somit für die Geschwindigkeit tatsächlich keine Rolle spielt. Man könnte nun annehmen, dass die Geschwindigkeit nicht relativ, sondern für jeden Beobachter gleich ist. Aber auch dies stellt sich als falsch heraus, wenn man einen dritten Beobachter fragt, der dem Jogger mit gleicher Geschwindigkeit hinterherläuft. Dieser dritte Beobachter wird nämlich behaupten, dass der Jogger sich nicht von ihm entfernt und daher die Geschwindigkeit Null hat. Die Geschwindigkeit ist demnach ebenfalls abhängig vom Bezugssystem des Beobachters.
Inertialsysteme
Die ruhenden Bezugssysteme der Beobachter auf den Bänken und das mitbewegte Bezugssystem des dritten Beobachters bezeichnet man als Inertialsysteme. Inertialsysteme sind Bezugssysteme, die gegeneinander verschoben sind (Beobachter 1 und 2) oder sich mit konstanter Geschwindigkeit geradlinig bewegen (Beobachter 3). Die Gesetze der Physik sind in jedem Inertialsystem gleich. Es gibt physikalische Größen wie den Ort oder die Geschwindigkeit, die abhängig vom Bezugssystem sind. Es gibt aber auch Größen, die in jedem Inertialsystem gleich sind. Solche Größen nennt man invariant. Im Beispiel ist die Beschleunigung $a$ invariant. Dies ist leicht einzusehen, wenn du das Geschwindigkeit-Zeit-Gesetz ableitest. Dann fällt nämlich die Geschwindigkeit $v_0$ der Beobachter ebenfalls weg. Da die Beschleunigung invariant ist, gilt dies auch für das 2. Newton'sche Axiom: $F=ma$. Dieses und jedes andere physikalische Gesetz ist also tatsächlich unabhängig vom Bezugssystem des Beobachters.
Galilei-Transformation und Scheinkräfte
Möchtest du bei der Beschreibung eines physikalischen Vorgangs von einem Inertialsystem in ein anderes wechseln, so wendest du die Galilei-Transformation an. Sind beide Inertialsysteme in x-Richtung gegeneinander verschoben oder entfernen sie sich in x-Richtung mit konstanter Geschwindigkeit voneinander, so lautet die Galilei-Transformation:
$ x'=x-vt \text{ , } y'=y \text{ , } z'=z \text{ , } t'=t $.
Dabei stehen die gestrichenen Größen für das Inertialsystem, in das du wechseln möchtest, die ungestrichenen Größen für das aktuelle Bezugssystem. Da beide in x-Richtung verschoben sind, bleiben die y- und z-Koordinaten sowie die Zeit natürlich unverändert.
Scheinkräfte
Du weißt nun, dass die physikalischen Gesetze in jedem Inertialsystem, also in jedem gleichförmig bewegten Bezugssystem, gleich sind. Dies trifft allerdings nicht auf beschleunigte Bezugssysteme zu. Beschleunigte Bezugssysteme sind Systeme, die ihren Geschwindigkeitsvektor ändern. Damit zählen auch rotierende Systeme zu den beschleunigten Bezugssystemen. Wechselst du von einem beschleunigten System in ein Inertialsystem oder umgekehrt, so gelten die physikalischen Gesetze nicht mehr. Dies äußert sich im Auftreten von sogenannten Scheinkräften.
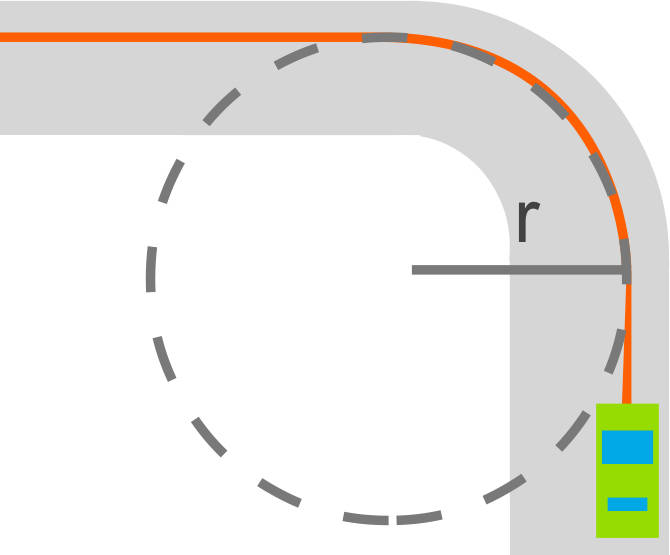
Die wohl bekannteste Scheinkraft ist die Zentrifugalkraft. Sitzt du in einem Auto, das sich mit konstanter Geschwindigkeit fortbewegt, befindest du dich in einem Inertialsystem. Fährt dieses Auto nun um die Kurve (Rotation um Kreismittelpunkt) ist es kein Inertialsystem mehr. Du als Beobachter hast das Gefühl nach außen gedrückt zu werden, obwohl das Auto eigentlich in Richtung Kreismittelpunkt nach innen beschleunigt wird. Tatsächlich ist es aber keine Kraft, die auf dich wirkt, sondern die Trägheit, die sich bemerkbar macht, denn du befindest dich noch im Inertialsystem, das sich geradlinig fortbewegt. Auch die Corioliskraft, die für die Spiralbahn von Luftmassen verantwortlich ist, die du von Wetterkarten kennst, ist eine Scheinkraft, die auf das rotierende Bezugssystem Erde zurückzuführen ist.
Alle Videos und Lerntexte zum Thema
Videos und Lerntexte zum Thema
Translationsbewegungen, Trägheit und Bezugssystem (3 Videos, 4 Lerntexte)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Translationsbewegungen, Trägheit und Bezugssystem (3 Arbeitsblätter)
Beliebteste Themen in Physik
- Temperatur
- Schallgeschwindigkeit
- Dichte
- Drehmoment
- Transistor
- Lichtgeschwindigkeit
- Elektrische Schaltungen – Übungen
- Galileo Galilei
- Rollen- Und Flaschenzüge Physik
- Radioaktivität
- Aufgaben zur Durchschnittsgeschwindigkeit
- Lorentzkraft
- Beschleunigung
- Gravitation
- Ebbe und Flut
- Hookesches Gesetz Und Federkraft
- Elektrische Stromstärke
- Elektrischer Strom Wirkung
- Reihenschaltung
- Ohmsches Gesetz
- Freier Fall
- Kernkraftwerk
- Reflexionsgesetz: Ebener Spiegel – Übungen
- Was sind Atome
- Aggregatzustände
- Infrarot, Uv-Strahlung, Infrarot Uv Unterschied
- Isotope, Nuklide, Kernkräfte
- Transformator
- Lichtjahr
- Si-Einheiten
- Fata Morgana
- Gammastrahlung, Alphastrahlung, Betastrahlung
- Kohärenz Physik
- Mechanische Arbeit
- Schall
- Elektrische Leistung
- Dichte Luft
- Ottomotor Aufbau
- Kernfusion
- Trägheitsmoment
- Heliozentrisches Weltbild
- Energieerhaltungssatz Fadenpendel
- Linsen Physik
- Ortsfaktor
- Interferenz
- Diode und Photodiode
- Wärmeströmung (Konvektion)
- Schwarzes Loch
- Frequenz Wellenlänge
- Elektrische Energie









 Bewegungen beobachten – Bezugssystem
Bewegungen beobachten – Bezugssystem
 Inertialsysteme und beschleunigte Bezugssysteme – Galilei-Transformation
Inertialsysteme und beschleunigte Bezugssysteme – Galilei-Transformation
 Rotierende Bezugssysteme und Inertialsysteme
Rotierende Bezugssysteme und Inertialsysteme









