Vektorielle Darstellung von Bewegungen
Mehrdimensionale physikalische Größen und insbesondere Größen der Bewegung müssen vektoriell dargestellt werden.
Inhaltsverzeichnis zum Thema
- Skalar und Vektor
- Größen in der Physik
- Bewegungen im Ein- und Mehrdimensionalen
- Mit vektoriellen Größen rechnen
- Multiplikation von einem Vektor mit einem Skalar
- Addition von Vektoren
- Multiplikation von Vektoren
Skalar und Vektor
Schon in der Grundschule hast du gelernt, was Zahlen sind, und wie du mit ihnen rechnen kannst. Solche Zahlen werden auch Skalare genannt. Später hast du sicher auch etwas von so genannten Vektoren gehört. Ein Vektor hat eine bestimmte Länge, eine dazugehörige Richtung, und beschreibt damit eine Parallelverschiebung in der Ebene oder im Raum.
Und was hat das jetzt alles mit Physik zu tun?
Größen in der Physik
In der Physik begegnen dir skalare und vektorielle Größen.
Skalare Größen können mit einem Skalar, also einer Zahl, und einer Einheit vollständig beschrieben werden. Sie werden auch ungerichtete Größen genannt. Zu den skalaren Größen gehören zum Beispiel der Druck oder die Masse.
Vektorielle Größen haben zu einem Betrag und einer Einheit auch immer noch eine Richtung. Sie werden deswegen auch gerichtete Größen genannt. Diese Informationen sind notwendig, um die Größe vollständig und unmissverständlich zu beschreiben. Sie werden durch einen Pfeil über dem Formelzeichen gekennzeichnet. Beispiele dafür sind die Kraft $\vec{F}$ oder die Geschwindigkeit $\vec{v}$. Besonders Größen, die eine Bewegung beschreiben, gehören zu den vektoriellen Größen. Dazu gehören neben der Vektorgröße Geschwindigkeit auch der Weg und die Beschleunigung.

Bewegungen im Ein- und Mehrdimensionalen
Im Eindimensionalen werden Vektoren häufig nicht als solche gekennzeichnet, da sie sich dort wie skalare Größen verhalten. Du hast bestimmt schon häufiger mit Geschwindigkeiten oder Beschleunigungen gerechnet, ohne die Vektorrechnung zu gebrauchen.
Da es sich um Bewegungen entlang einer Linie handelt, kann die Bewegung nur vor- oder rückwärts erfolgen. Die Bewegung, zum Beispiel eine Geschwindigkeit, kann durch eine Komponente vollständig beschrieben werden.
$\vec{v}=v_x$
Im Mehrdimensionalen, also zwei- oder dreidimensional, ist dies nicht so einfach. Sobald sich ein Körper in der Ebene oder im Raum bewegt, musst du die vektorielle Darstellung nutzen. Sie hat (je nach Dimension) zwei oder drei Komponenten.
$\vec{v}=\left( \begin{matrix} v_x \\ v_y \\ v_z \end{matrix} \right) $
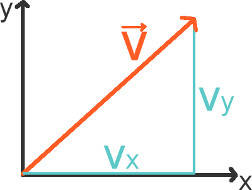
Der Betrag eines Vektors wird durch Betragsstriche oder durch Weglassen des Pfeils über dem Formelzeichen gekennzeichnet. Er wird im Allgemeinen mit der Formel
$|\vec{v}|=v=\sqrt{{v_x}^2+{v_y}^2+{v_z}^2}$
berechnet. Der Betrag entspricht der Länge des Vektorpfeils.
Mit vektoriellen Größen rechnen
Das Rechnen mit vektoriellen Größen erfolgt wie in der Mathematik. Es müssen dabei ein paar spezielle Rechenregeln befolgt werden.
Multiplikation von einem Vektor mit einem Skalar
Um einen Vektor mit einem Skalar zu multiplizieren, wird das Skalar mit jeder Komponente des Vektors einzeln multipliziert.
$\vec{v}\cdot a=\left( \begin{matrix} v_x \cdot a \\ v_y \cdot a \\ v_z \cdot a\end{matrix} \right) ~,a \in \mathbb{R} $
Diese Multiplikation kann auch graphisch erfolgen. Da die Länge des Vektorpfeils durch seinen Betrag angegeben wird, muss der Betrag mit dem Skalar multipliziert werden und der Pfeil entsprechend verlängert werden.
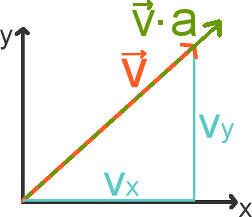
Die Division erfolgt analog zur Multiplikation.
Addition von Vektoren
Vektoren werden Komponentenweise addiert.
$\vec{v_1} +\vec{v_2} =\left( \begin{matrix} v_{1x} \\ v_{1y} \\ v_{1z} \end{matrix} \right) + \left( \begin{matrix} v_{2x} \\ v_{2y} \\ v_{2z} \end{matrix} \right) = \left( \begin{matrix} v_{1x}+v_{2x} \\ v_{1y}+v_{2y} \\ v_{1z}+v_{2z} \end{matrix} \right)$
Auch die Addition kann graphisch durchgeführt werden. Dabei werden die Pfeile parallel verschoben und aneinander angefügt. Es ergibt sich ein resultierender Vektor:
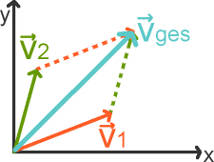
Die Subtraktion erfolgt analog zur Addition.
Multiplikation von Vektoren
Es können auch Vektoren miteinander multipliziert werden. Dafür müssen das Kreuzprodukt (auch Vektorprodukt) oder das Skalarprodukt gebildet werden. Bei dem Kreuzprodukt von zwei Vektoren wird als Ergebnis ein Vektor erhalten, beim Skalarprodukt ein Skalar. Dies wird dir bei Bewegungen kaum begegnen, jedoch sind andere (skalare) Größen wie die Arbeit durch ein Skalarprodukt definiert. Es bleibt also spannend.
Alle Videos zum Thema
Videos zum Thema
Vektorielle Darstellung von Bewegungen (2 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Vektorielle Darstellung von Bewegungen (2 Arbeitsblätter)
Beliebteste Themen in Physik
- Temperatur
- Schallgeschwindigkeit
- Dichte
- Drehmoment
- Transistor
- Lichtgeschwindigkeit
- Elektrische Schaltungen – Übungen
- Galileo Galilei
- Rollen- Und Flaschenzüge Physik
- Radioaktivität
- Aufgaben zur Durchschnittsgeschwindigkeit
- Lorentzkraft
- Beschleunigung
- Gravitation
- Ebbe und Flut
- Hookesches Gesetz Und Federkraft
- Elektrische Stromstärke
- Elektrischer Strom Wirkung
- Reihenschaltung
- Ohmsches Gesetz
- Freier Fall
- Kernkraftwerk
- Reflexionsgesetz: Ebener Spiegel – Übungen
- Was sind Atome
- Aggregatzustände
- Infrarot, Uv-Strahlung, Infrarot Uv Unterschied
- Isotope, Nuklide, Kernkräfte
- Transformator
- Lichtjahr
- Si-Einheiten
- Fata Morgana
- Gammastrahlung, Alphastrahlung, Betastrahlung
- Kohärenz Physik
- Mechanische Arbeit
- Schall
- Elektrische Leistung
- Dichte Luft
- Ottomotor Aufbau
- Kernfusion
- Trägheitsmoment
- Heliozentrisches Weltbild
- Energieerhaltungssatz Fadenpendel
- Linsen Physik
- Ortsfaktor
- Interferenz
- Diode und Photodiode
- Wärmeströmung (Konvektion)
- Schwarzes Loch
- Frequenz Wellenlänge
- Elektrische Energie



 Vektorgröße – Geschwindigkeit
Vektorgröße – Geschwindigkeit
 Bewegungen – vektorielle Darstellung
Bewegungen – vektorielle Darstellung









