Wellenoptik und Quantenphysik
Quantenobjekte lassen sich auf ein Energiequant reduzieren, welches durch Überlagerung von Wellenfunktionen entsteht.
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Ein Leben als Photon
- Quantenobjekte
- Doppelspaltversuch
- Experimente mit Quantenobjekten
- Heisenbergsche Unbestimmtheitsrelation
Ein Leben als Photon
Als Photon wärst du immer mit Lichtgeschwindigkeit unterwegs und, wenn dich einmal die Polizei herauswinken würde, hättest du immer eine Ausrede parat. Denn wenn die Polizei behaupten würde, dass du zu schnell wärst, wärst du einfach nicht zu dieser Zeit an diesem Ort gewesen. Wenn sie aber nachweisen könnten, dass du dort wärst, könnten sie keine Aussagen zu deiner Geschwindigkeit machen. Folglich könnten sie dich nicht bestrafen. Warum das aber nur für Quantenobjekte gilt und nicht für dich im realen Straßenverkehr, werde ich dir nun erklären.
Quantenobjekte
Nach der Quantenmechanik lässt sich jedes Photon als Wellenfunktion eindeutig beschreiben. Ein Lichtstrahl besteht aus vielen dieser einzelnen Photonen, diese überlagern sich. Überlagern sich nun sehr viele Wellenfunktionen mit relativ ähnlicher Frequenz, wird die Wellenfunktion der Überlagerung aussehen wie eine lange Gerade mit einer einzelnen, lokal begrenzten, ausgeprägten Schwingung. Sie ist also ein einzelnes Energiepaket, welches sich durch Zeit und Raum bewegt. Dies ist ein Energiequant. Ein Photon ist ein solches Energiequant. Quantenobjekte können auf ein solches Quant reduziert werden.
Dies trifft nur auf sehr kleine massearme Objekte, insbesondere Elementarteilchen zu. Aber auch langsame Moleküle mit einer daher großen De-Broglie-Wellenlänge können als Quantenobjekte betrachtet werden.
Doppelspaltversuch
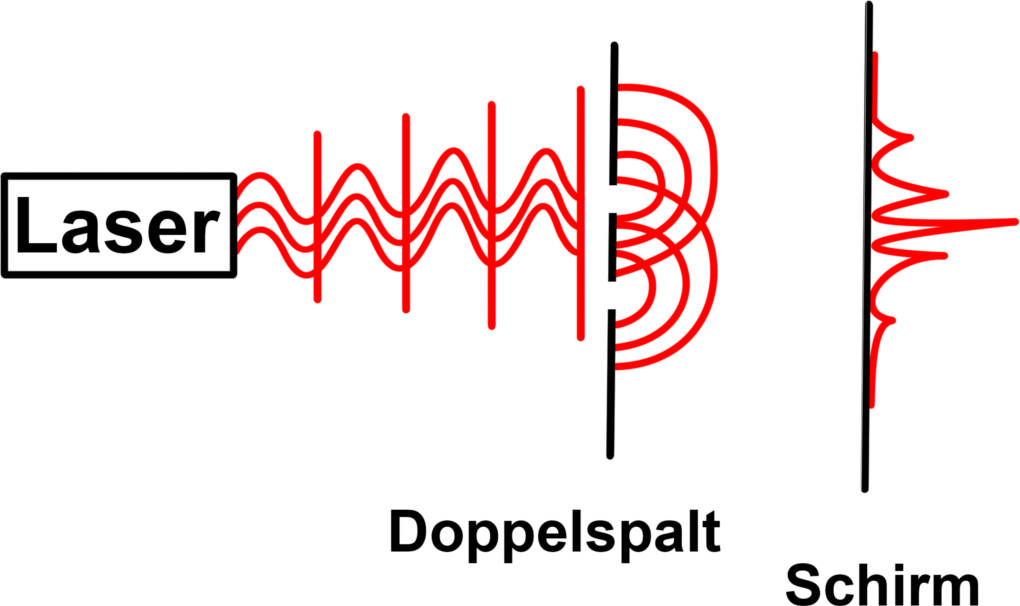
Durch den Doppelspaltversuch mit Elektronen konnte nachgewiesen werden, dass diese genau wie Photonen interferieren können. Das Interferenzmuster, das durch Beugung und Interferenz des Lichtes am Doppelspalt entsteht, wird sichtbar, wenn sowohl der Spaltabstand $d$ wie auch die Entfernung zum Schirm $e$ passend zur De-Broglie-Wellenlänge $\lambda_\text{de-Broglie}$ der Elektronen ausgewählt wird:
$a\approx\lambda_\text{de-Broglie} \cdot \dfrac{e}{d}$.
$a$ ist dann der Abstand zwischen dem Maximum 0. und 1. Ordnung. Die De-Broglie-Wellenlänge lässt sich über die Beschleunigungsspannung $U_B$ sehr gut einstellen.
$\lambda_\text{de-Broglie}=\dfrac{h}{\sqrt{2m_e \cdot e \cdot U_B}}=\dfrac{h}{\sqrt{2m_e \cdot E_{kin}}}$
Experimente mit Quantenobjekten
Für ein Experiment mit einem klassischen Teilchen, welches immer gleich ausgeführt wird, sind die Messergebnisse determiniert (vorherbestimmt). Dies bedeutet, dass man eindeutig berechnen kann, wo sich das Teilchen wann befinden wird.
Für ein Experiment mit einem Quantenobjekt, welches immer gleich ausgeführt wird, sind die Wahrscheinlichkeiten der Messergebnisse determiniert. Dies bedeutet, dass man nur sagen kann, wo sich das Quantenobjekt mit der größten Wahrscheinlichkeit zu einem bestimmten Zeitpunkt $t$ aufhalten wird.
Die Aufgabe der Quantenmechanik ist es, diese Wahrscheinlichkeit zu berechnen und durch eine Welle zu beschreiben, während wir durch die Messung das Quantenobjekt als Teilchen identifizieren können. Da Quantenobjekte sowohl Teilchen- wie auch Welleneigenschaften besitzen, sind sie ein gutes Beispiel für den Welle-Teilchen-Dualismus.
Heisenbergsche Unbestimmtheitsrelation

Da sich jedes Quant nur als Überlagerung von Wellen mit unterschiedlichen Frequenzen darstellen lässt, die als Überlagerung eine neue Wellenfunktion bilden, lässt sich auch die Frequenz des Quants nur mit einem Frequenzintervall angeben. Dadurch lässt sich der Energiewert und der Impuls des Teilchens nicht mehr genau angeben:
$\Delta E=h\cdot \Delta f$
$\Delta p=\frac{h}{v} \cdot \Delta f$
Durch die vielseitige Entsprechung (Komplementarität) der physikalischen Größen in der Quantentheorie lassen sich auch Aussagen über die Geschwindigkeit und den Ort eines Quantenobjektes machen. Mit der akustischen Unschärferelation $\Delta f \cdot \Delta t =½$ zeigt sich, dass, wenn wir das Energieintervall $\Delta E$ des Quants möglichst genau angeben wollen, der Zeitparameter sehr ungenau werden muss.
$\Delta W \Delta t = \dfrac{h}{2}$
Und wenn wir versuchen, die Impulsunschärfe $\Delta p$ möglichst klein anzugeben, wird die Ortsunschärfe $\Delta x$ sehr groß.
$\Delta p \Delta x = \dfrac{h}{2}$
Durch die Symmetrie dieser Größen zueinander, lässt sich natürlich auch umgekehrt argumentieren. Dies ist die Heisenbergsche Unbestimmtheitsrelation, auch Heisenbergsche Unschärferelation genannt.
Alle Videos und Lerntexte zum Thema
Videos und Lerntexte zum Thema
Wellenoptik und Quantenphysik (5 Videos, 1 Lerntext)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Wellenoptik und Quantenphysik (5 Arbeitsblätter)
Beliebteste Themen in Physik
- Temperatur
- Schallgeschwindigkeit
- Dichte
- Drehmoment
- Transistor
- Lichtgeschwindigkeit
- Elektrische Schaltungen – Übungen
- Galileo Galilei
- Rollen- Und Flaschenzüge Physik
- Radioaktivität
- Aufgaben zur Durchschnittsgeschwindigkeit
- Lorentzkraft
- Beschleunigung
- Gravitation
- Ebbe und Flut
- Hookesches Gesetz Und Federkraft
- Elektrische Stromstärke
- Elektrischer Strom Wirkung
- Reihenschaltung
- Ohmsches Gesetz
- Freier Fall
- Kernkraftwerk
- Reflexionsgesetz: Ebener Spiegel – Übungen
- Was sind Atome
- Aggregatzustände
- Infrarot, Uv-Strahlung, Infrarot Uv Unterschied
- Isotope, Nuklide, Kernkräfte
- Transformator
- Lichtjahr
- Si-Einheiten
- Fata Morgana
- Gammastrahlung, Alphastrahlung, Betastrahlung
- Kohärenz Physik
- Mechanische Arbeit
- Schall
- Elektrische Leistung
- Dichte Luft
- Ottomotor Aufbau
- Kernfusion
- Trägheitsmoment
- Heliozentrisches Weltbild
- Energieerhaltungssatz Fadenpendel
- Linsen Physik
- Ortsfaktor
- Interferenz
- Diode und Photodiode
- Wärmeströmung (Konvektion)
- Schwarzes Loch
- Frequenz Wellenlänge
- Elektrische Energie









 Teilchen als Welle
Teilchen als Welle
 Interferenz und Photonen
Interferenz und Photonen
 Elektronenbeugung am Doppelspalt
Elektronenbeugung am Doppelspalt
 Unbestimmtheitsrelation
Unbestimmtheitsrelation
 Quanteninterferenz
Quanteninterferenz









