Elektromagnetischer Schwingkreis
Aufbau und Ablauf der vier Phasen eines elektromagnetischen Schwingkreises und Vergleich mit dem Fadenpendel und Schwingdauer
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Wozu braucht man sowas?
- Aufbau eines elektromagnetischen Schwingkreises
- Der elektromagnetische Schwingungsvorgang im Schwingkreis
- Phase 1
- Phase 2
- Phase 3
- Phase 4
Wozu braucht man sowas?
Ein elektromagnetischer Schwingkreis erzeugt elektromagnetische Wellen, die viele Anwendungen haben. Das Spektrum an elektromagnetischen Wellen reicht von Röntgenstrahlen, die in der Medizin von großer Bedeutung sind, über Funk- und Radiowellen zur Kommunikation bis zu Mikrowellen, die der Namensgeber des Bauteils sind, das in jedem Haushalt zu finden ist.
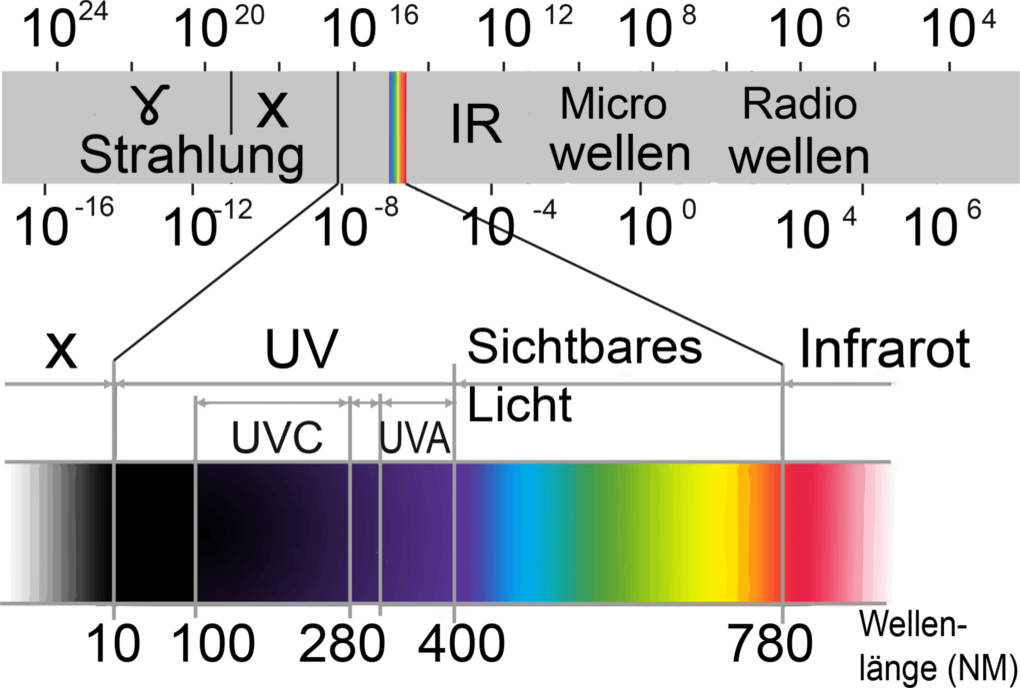
Ebenso werden elektromagnetische Schwingkreise in Form von Hertz'scher Dipolen in der Antennentechnik verwendet. Wie du siehst, sind elektromagnetische Wellen ein fester Bestandteil moderner Technik. Daher macht es Sinn, sich mit dem elektromagnetischen Schwingkreis zu beschäftigen.
Aufbau eines elektromagnetischen Schwingkreises
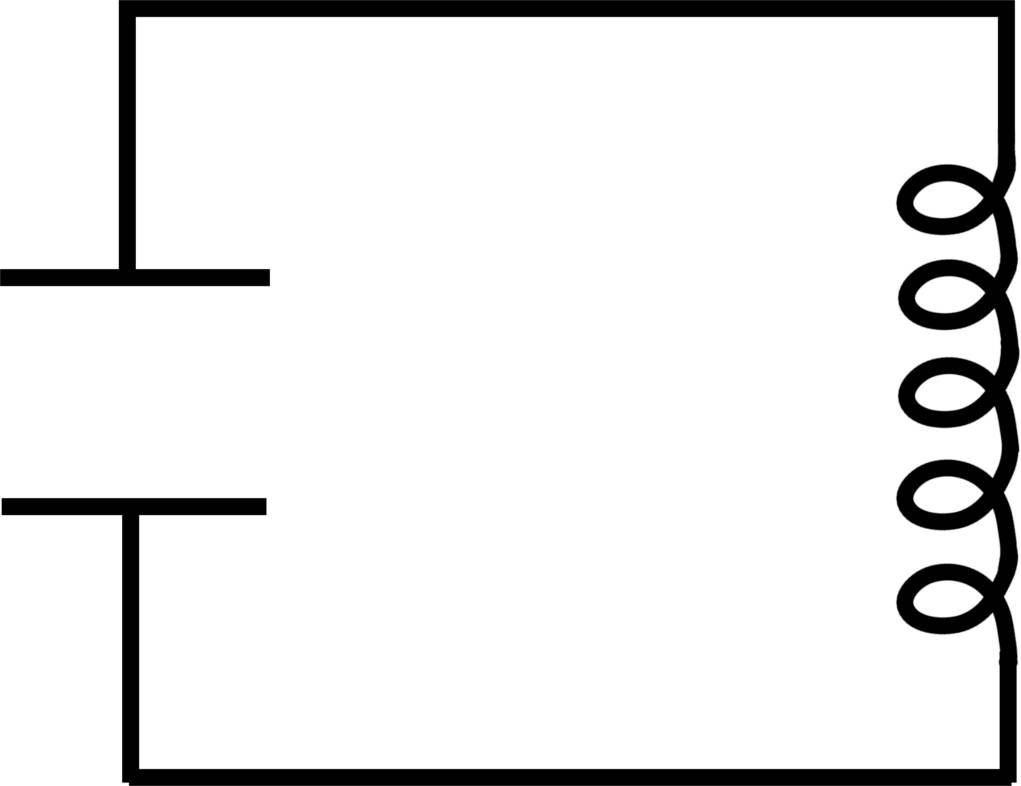
Zentrale Bauelemente eines elektromagnetischen Schwingkreises sind eine Spule mit Induktivität $L$ und ein Kondensator mit Kapazität $C$. Ein solcher Schwingkreis wird daher auch als LC-Schwingkreis bezeichnet. Die Spule und der Kondensator sind in Reihe geschaltet. Idealisiert betrachtet, haben weder die Bauteile noch die Kabel einen elektrischen Widerstand. In der Realität gibt es natürlich immer einen elektrischen Widerstand, es sei denn der Schwingkreis ist supraleitend. Die diversen Widerstände eines realen Schwingkreises werden dann durch einen Ersatzwiderstand $R$ ausgedrückt, der ebenfalls in Reihe geschaltet ist. Hat ein elektromagnetischer Schwingkreis einen Widerstand, so verringert sich die Energie des Schwingkreises durch Wärmeentwicklung. Durch eine Meißner-Schaltung kann dem entgegengewirkt werden. Hier wird aber nur der ideale Schwingkreis betrachtet, sodass du von $R=0\Omega$ ausgehen kannst.
Der elektromagnetische Schwingungsvorgang im Schwingkreis
Du hast bereits gelernt, dass Schall eine mechanische Welle ist. Ebenso kennst du Feder- und Fadenpendel. All diese Beispiele führen wie auch ein elektromagnetischer Schwingkreis Schwingungen aus, sodass es im Folgenden immer wieder Analogien zwischen der elektromagnetischen Schwingung und dem Pendel geben wird. Jede Schwingung ist dabei in vier Phasen unterteilt. Die vier Phasen bilden eine halbe Periode der Schwingung.
Zu Beginn wird der Schwingkreis an eine Spannungsquelle angeschlossen, sodass sich der Kondensator auflädt. Das heißt, dass sich die beiden Kondensatorplatten entgegengesetzt aufladen, bis an ihnen dieselbe Spannung $U$ anliegt, die von der Spannungsquelle geliefert wird. Anschließend wird der Schwingkreis von der Spannungsquelle getrennt und sich selbst überlassen. Er kann idealisiert also weder zusätzliche Energie erhalten noch Energie verlieren. Dies entspricht dem Auslenken des Fadenpendels mit der Hand und anschließendem Loslassen.
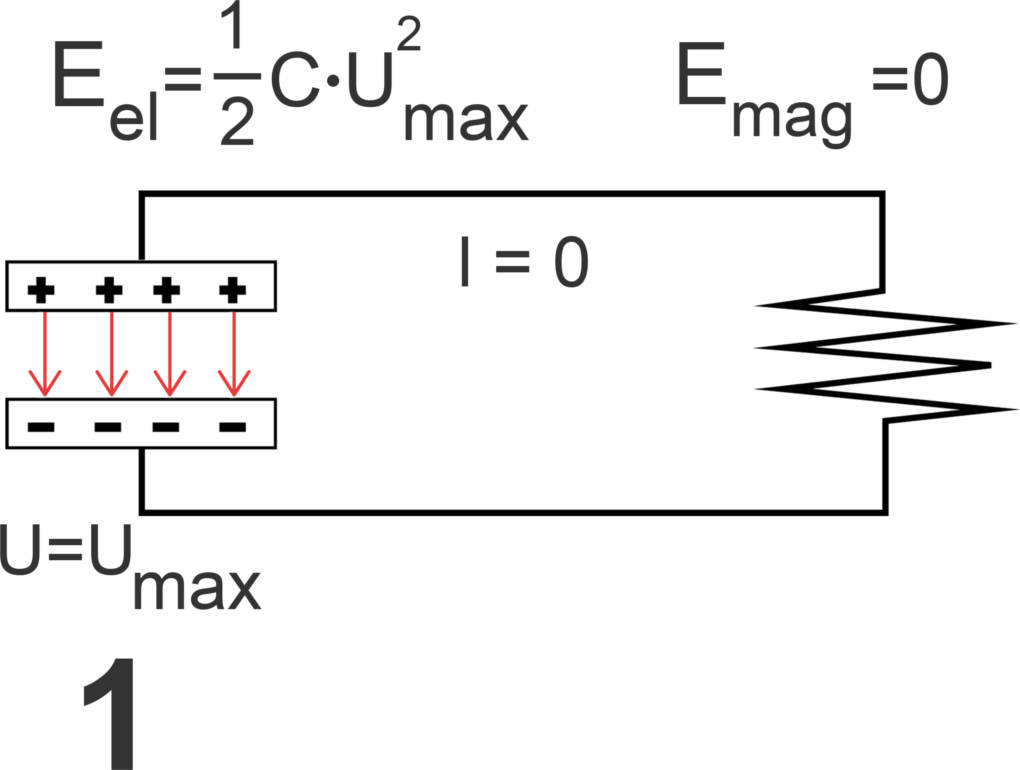
Phase 1
Die gesamte Energie des Schwingkreises ist zunächst in Form von elektrischer Energie im elektrischen Feld des Kondensators gespeichert. Die elektrische Energie ist
$ W_{el }= \frac{1}{2} C U^2 $
und es gilt
$W_{el}=W_{max}$.
Auch beim Fadenpendel ist im Moment des Loslassens die gesamte Energie in Form von potentieller Energie gespeichert, da es zu einer bestimmten Höhe ausgelenkt ist.
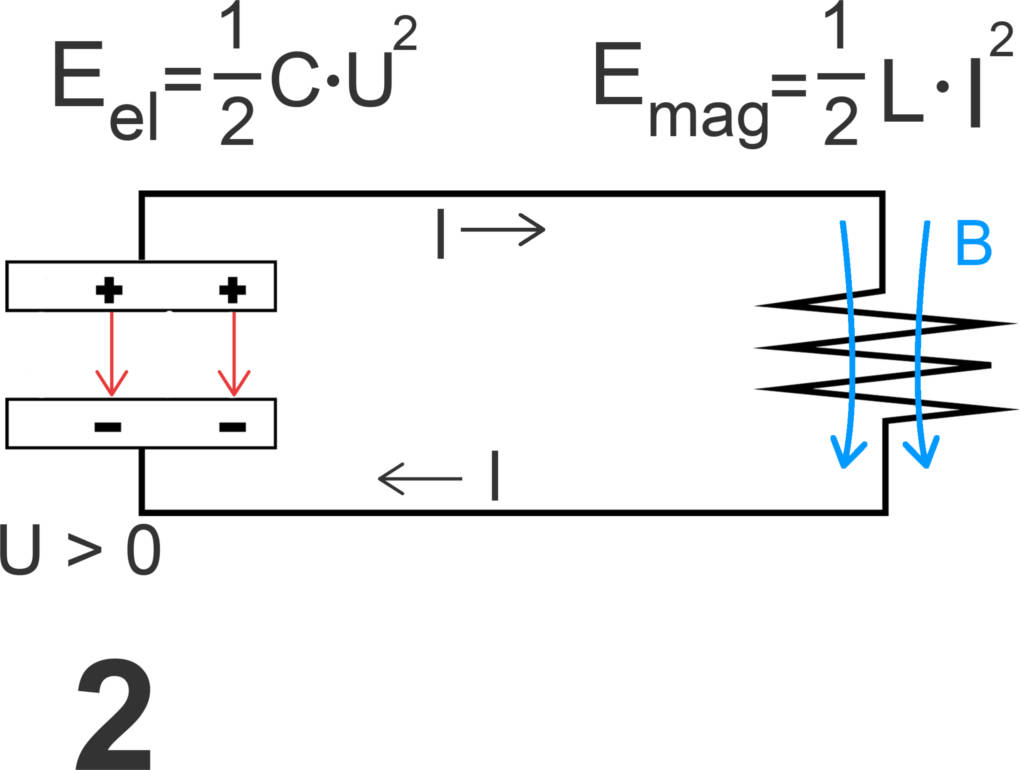
Phase 2
Die gegenteiligen Ladungen der beiden Kondensatorplatten versuchen sich nun auszugleichen, daher fließt ein Strom $I$ in physikalischer Stromrichtung von der negativen Platte zur positiven Platte und der Kondensator entlädt sich allmählich. Ohne Spule wäre der Kondensator kurzgeschlossen und würde sich sofort entladen. Da sich in dem Schwingkreis aber eine Spule befindet, durch die der Strom hindurchfließt, baut sich in der Spule allmählich ein Magnetfeld auf. Dieses Magnetfeld ist aufgrund der Lenz'schen Regel stets der Ursache seines Entstehens entgegengerichtet. Daher entlädt sich der Kondensator nur langsam. Die Energie des Schwingkreises teilt sich in elektrische und magnetische Energie auf.
$W_{mag}+W_{el}=W_{max}$.
Diese Phase entspricht beim Fadenpendel dem Beschleunigen des Pendels nach dem Loslassen, das dabei potentielle Energie verliert und kinetische Energie gewinnt.
Phase 3
In dem Moment, da der Kondensator sich vollständig entladen hat ($U=0 \text{V}$), ist der Stromfluss $I$ und damit die Stärke des Magnetfeldes in der Spule maximal. Das elektrische Feld des Kondensators hat sich vollständig abgebaut und speichert keine Energie mehr. Stattdessen ist die gesamte Energie des Schwingkreises in Form von magnetischer Energie im magnetischen Feld der Spule gespeichert. Die magnetische Energie ist
$ W_{mag}=\frac12 L I^2 $
und es gilt
$W_{mag}=W_{max}$.
Das Fadenpendel befindet sich in dieser Phase am tiefsten Punkt. Die potentielle Energie hat sich vollständig in kinetische Energie umgewandelt.
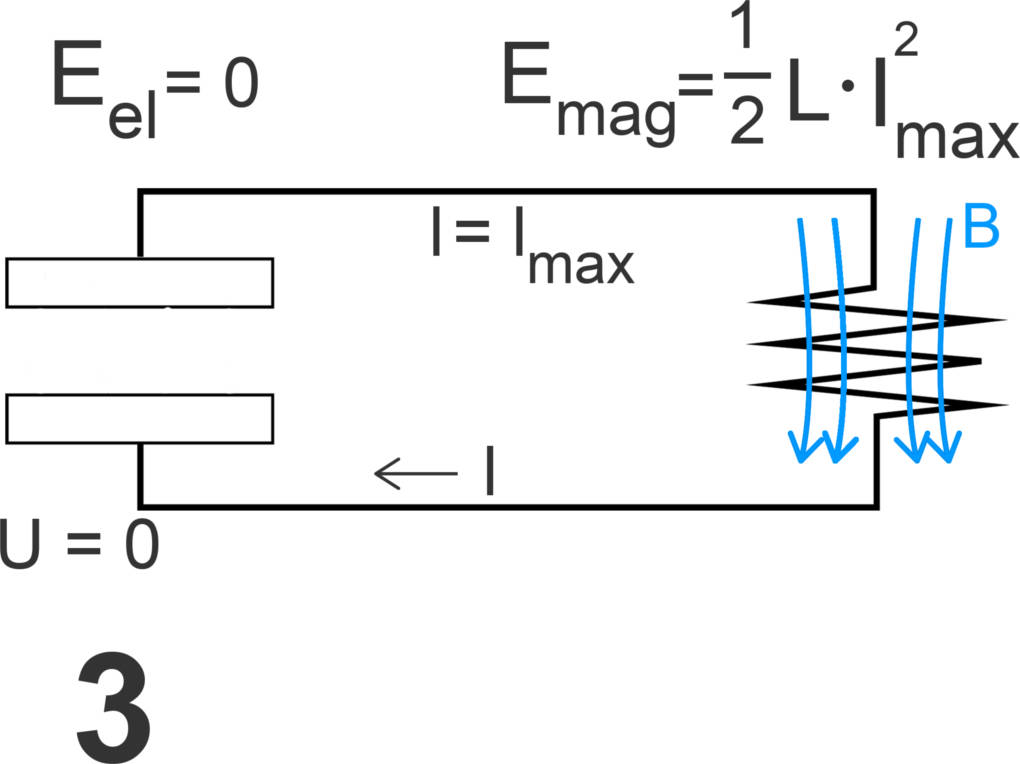
Phase 4
Da der Kondensator sich vollständig entladen hat, dürfte eigentlich kein Strom mehr fließen und das Magnetfeld in der Spule müsste verschwinden. Nun wirkt aber die Lenz'sche Regel der Abschwächung des Stroms entgegen, sodass der Strom noch weiterfließt. Das Magnetfeld in der Spule baut sich daher nur langsam ab und gleichzeitig wird der Kondensator mit gegenteiliger Polung wieder aufgeladen. In dieser Phase gilt also erneut
$W_{mag}+W_{el}=W_{max}$.
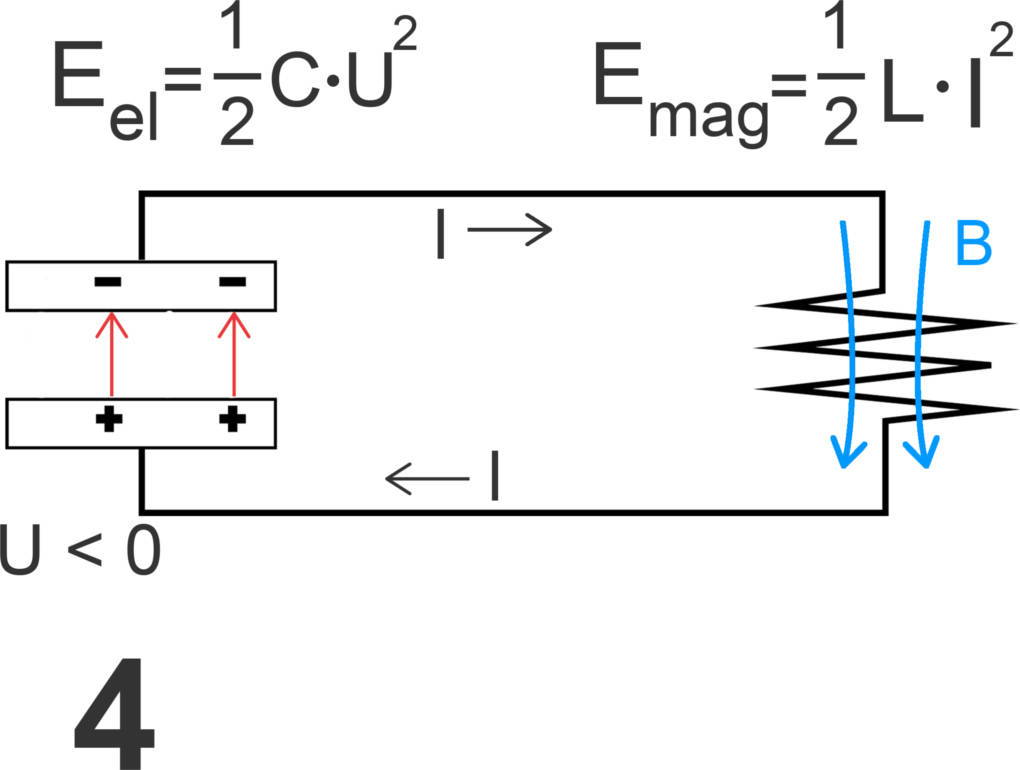
Diese Phase endet damit, dass sich das Magnetfeld der Spule komplett abgebaut hat ($I=0$) und stattdessen der Kondensator wieder voll aufgeladen ist. Danach beginnt der Schwingkreis von vorn, aber in entgegengesetzte Richtung.
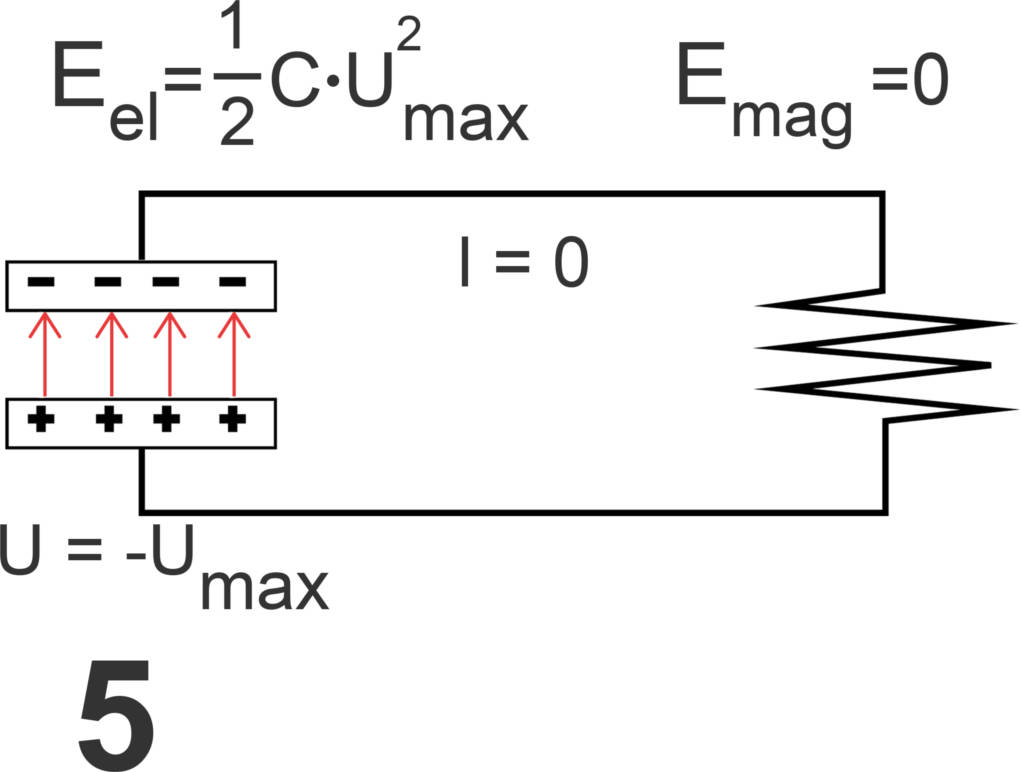
Das Fadenpendel verharrt ebenfalls nicht im tiefsten Punkt, sondern schwingt aufgrund seiner Geschwindigkeit solange weiter, bis es wieder seinen höchsten Punkt erreicht hat. Danach schwingt das Fadenpendel zurück.
Thomson'sche Schwingungsgleichung
Wie jede Schwingung hat auch der elektromagnetische Schwingkreis eine Schwingdauer oder Periode $T$. Im Fall des Schwingkreises kann diese über die Thomson'sche Schwingungsgleichung hergeleitet werden. Die Details der Herleitung sind Gegenstand einer aufbauenden Themenseite. Zunächst soll folgender Zusammenhang genügen: Die Schwingdauer wird mit zunehmender Kapazität des Kondensators größer, da der Kondensator mehr Ladung aufnehmen kann und somit länger zum Entladen braucht. Eine größere Induktivität der Spule bedeutet ebenfalls eine Vergrößerung der Schwingdauer, da der Einfluss der Lenz'schen Regel stärker wird und sich das Magnetfeld langsamer auf- bzw. abbaut. Es lässt sich herleiten, dass
$ T=2\pi\sqrt{LC} $.
Versuche dich doch selbst einmal an der Berechnung der Schwingungsdauer.
Alle Videos zum Thema
Videos zum Thema
Elektromagnetischer Schwingkreis (5 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Elektromagnetischer Schwingkreis (4 Arbeitsblätter)
Beliebteste Themen in Physik
- Temperatur
- Schallgeschwindigkeit
- Dichte
- Drehmoment
- Transistor
- Lichtgeschwindigkeit
- Elektrische Schaltungen – Übungen
- Galileo Galilei
- Rollen- Und Flaschenzüge Physik
- Radioaktivität
- Aufgaben zur Durchschnittsgeschwindigkeit
- Lorentzkraft
- Beschleunigung
- Gravitation
- Ebbe und Flut
- Hookesches Gesetz Und Federkraft
- Elektrische Stromstärke
- Elektrischer Strom Wirkung
- Reihenschaltung
- Ohmsches Gesetz
- Freier Fall
- Kernkraftwerk
- Reflexionsgesetz: Ebener Spiegel – Übungen
- Was sind Atome
- Aggregatzustände
- Infrarot, Uv-Strahlung, Infrarot Uv Unterschied
- Isotope, Nuklide, Kernkräfte
- Transformator
- Lichtjahr
- Si-Einheiten
- Fata Morgana
- Gammastrahlung, Alphastrahlung, Betastrahlung
- Kohärenz Physik
- Mechanische Arbeit
- Schall
- Elektrische Leistung
- Dichte Luft
- Ottomotor Aufbau
- Kernfusion
- Trägheitsmoment
- Heliozentrisches Weltbild
- Energieerhaltungssatz Fadenpendel
- Linsen Physik
- Ortsfaktor
- Interferenz
- Diode und Photodiode
- Wärmeströmung (Konvektion)
- Schwarzes Loch
- Frequenz Wellenlänge
- Elektrische Energie







 Elektrischer Schwingkreis – Aufbau und Ablauf
Elektrischer Schwingkreis – Aufbau und Ablauf
 Thomson'sche Schwingungsgleichung
Thomson'sche Schwingungsgleichung
 Meißner-Schaltung
Meißner-Schaltung
 Hertzscher Dipol
Hertzscher Dipol









