Kinetische Gastheorie

Inhaltsverzeichnis zum Thema

• Einleitung und Grundlagen
• Der Druck im Teilchenmodell (1. Form der kinetischen Gastheorie)
• Die 2. und 3. Form der kinetischen Gastheorie
• Die 3. Form der kinetischen Gastheorie

Einleitung und Grundlagen

Die Kinetische Gastheorie beschreibt den Zustand und das Verhalten eines idealen Gases. Der Theorie nach besteht ein Gas aus sehr vielen kleinen Teilchen (Atomen oder Molekülen) mit einer bestimmten Masse $m$, die sich mit einer bestimmten Geschwindigkeit $\vec{v}$ bewegen. In einem idealen Gas sind diese Teilchen punktförmig (ohne räumliche Ausdehnung) und bewegen sich zufällig und unabhängig voneinander. Untereinander oder mit einer Wand stoßen sie elastisch.

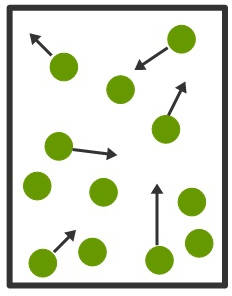
Die kinetischen Gastheorie erklärt mittels mikroskopischer Teilcheneigenschaften wie Energie, Impuls und Teilchenzahl die makroskopischen Zustandsgrößen Druck und Temperatur eines Gases. In der Grundgleichung der kinetischen Gastheorie, auf die noch eingegangen wird, werden also die Zustandsgrößen der Thermodynamik mit den Eigenschaften der kleinsten Teilchen in direkte Verbindung gesetzt.

Da ein Gas aus etlichen kleinen Teilchen besteht, ist es unmöglich zu sagen, welches Teilchen sich gerade mit welcher Geschwindigkeit in welche Richtung bewegt. Allerdings lässt sich beispielsweise die mittlere Energie $\overline{E_{kin}}$, die mittlere Geschwindigkeit $\overline{\vec{v}}$ oder auch die wahrscheinlichste Geschwindigkeit eines Teilchens bestimmen. Die kinetische Gastheorie behandelt also Wahrscheinlichkeitsgrößen und wird daher der statistischen Physik zugeordnet.

Der Druck im Teilchenmodell (1. Form der kinetischen Gastheorie)

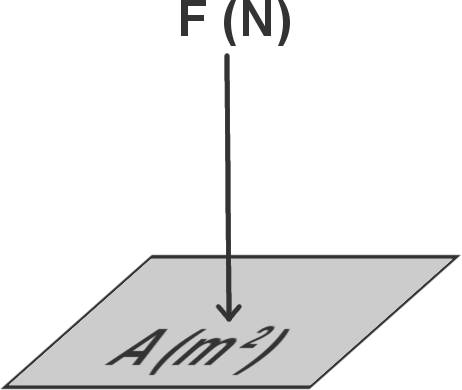
Der Druck $p$ ist die Kraft $\vec{F}$, die auf eine Fläche $A$ wirkt. Die Kraft wiederum entspricht einer Änderung des Impulses pro Zeit (Impulsübertrag).

$p=\frac{\vec{F}}{A}$, $F=\frac{\Delta\vec{p}}{t}$

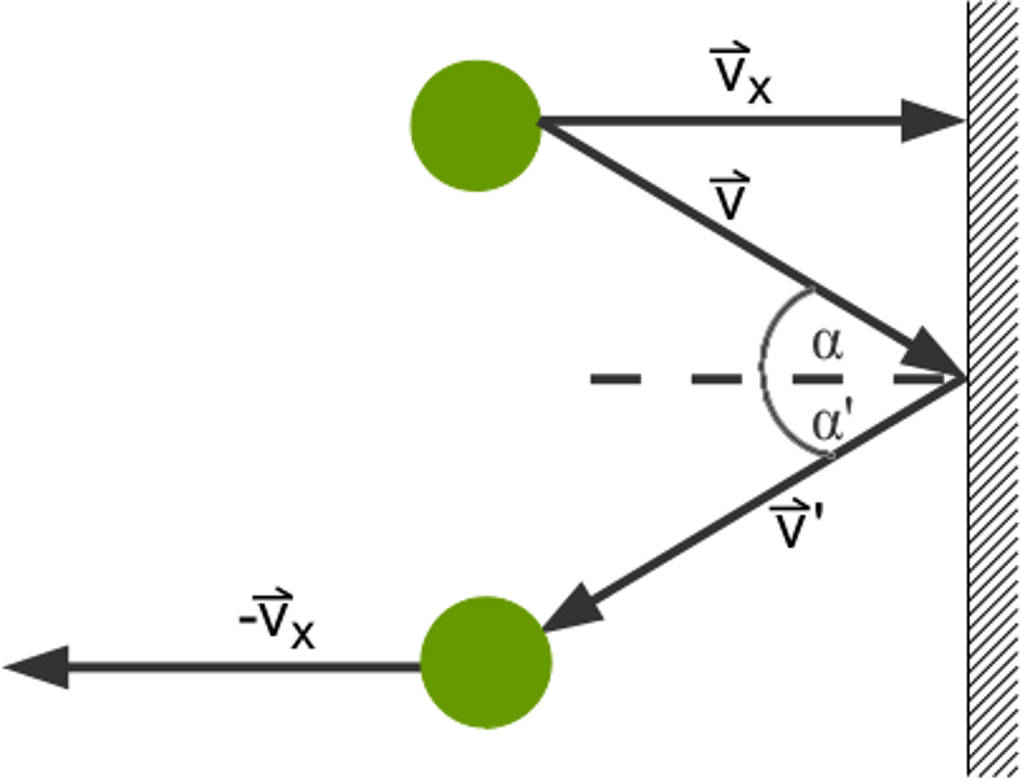
Stößt ein Teilchen in einem Quader mit Volumen $V$ nun elastisch gegen eine Wand, so prallt es ab und bewegt sich nun mit gleicher Geschwindigkeit wie zuvor aber in entgegensetzte Richtung. Es hat also ein Impulsübertrag und somit eine Kraftwirkung auf die Wand mit der Fläche $A$ stattgefunden (Druck). Da sich die Teilchen wild durcheinander bewegen und mit jeder Wand gleich oft stoßen, genügt es, zur Berechnung der Drucks eine einzige Wand zu betrachten. In x-Richtung ist der Impulsübertrag also

$\frac{\Delta p_x}{t}=\frac{m v_x - (-m v_x) }{t}= \frac{2m v_x}{t}$.

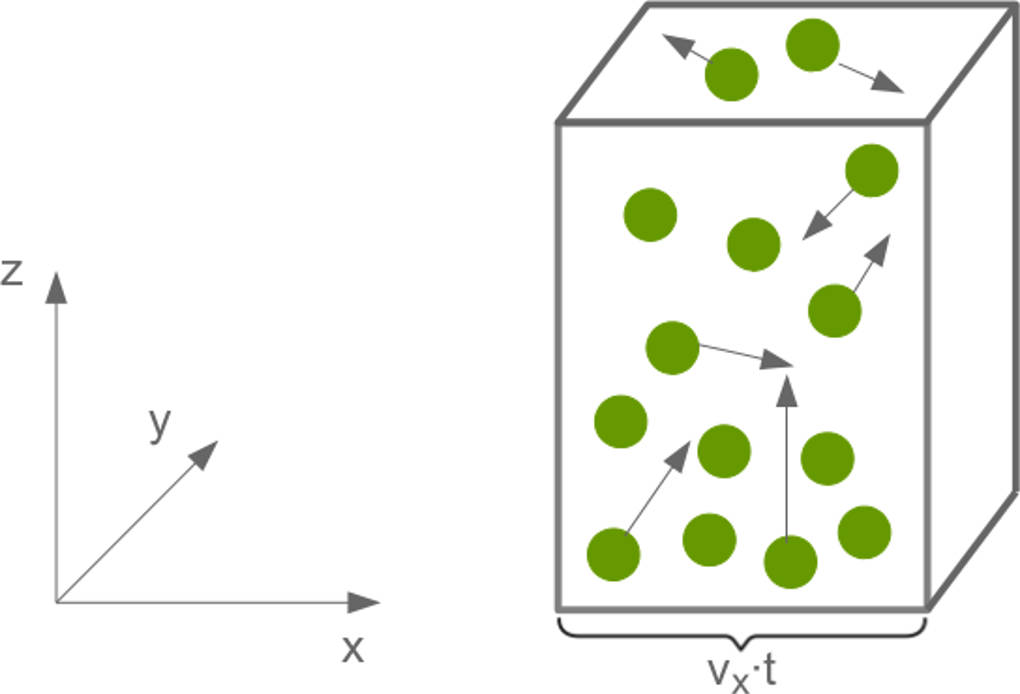
Im Mittel bewegen sich die Hälfte aller Teilchen nach rechts, die andere Hälfte nach links. Die Anzahl der Teilchen $N$, die die rechte Wand in der Zeit $t$ erreichen können, ist dann die halbe Teilchendichte $\frac12\frac{N}{V}$ multipliziert mit dem Volumen, das die Teilchen aufgrund ihrer Geschwindigkeit durchfliegen können.

$N=\frac12\frac{N}{V}\cdot A\cdot d=\frac12\frac{N}{V}\cdot A\cdot v_x t$

Der Druck im Quader im Teilchenmodell ist also die Gesamtkraft aller $N$ Teilchen auf die rechte Wand:

$p=N\cdot\frac{F}{A}=\frac{N}{V}m v_x^2$.

Die mittlere Geschwindigkeit $\overline{\vec{v}}$ ist ein Vektor mit einer Komponente für jede Raumrichtung. Im Schnitt ist jede Geschwindigkeitskomponente gleich groß. Daher wird im letzten Schritt noch die Ersetzung $\overline{v_x}^2=\frac13\overline{v}^2$ vorgenommen und es ergibt sich die 1. Form der kinetischen Gastheorie:

$pV=\frac13 N m \overline{v}^2$.

Die 2. und 3. Form der kinetischen Gastheorie

Die 1. Form der kinetischen Gastheorie gibt einen Zusammenhang zwischen den mikroskopischen Teilcheneigenschaften mittlere Geschwindigkeit und Masse und der makroskopischen Zustandsgröße Druck an. Im Folgenden siehst du, wie der Druck von der mittleren kinetischen Energie eines Teilchens abhängt. Dazu musst du die rechte Seite der Gleichung nur mit 2 erweitern und $\frac12 m \overline{v}$ durch $E_{kin}$ ersetzen.

$pV=\frac23 N \overline{E_{kin}}$

Dies ist die 2. Form der kinetischen Gastheorie.

Die 3. Form der kinetischen Gastheorie

Du kennst bereits die ideale Gasgleichung

$pV=N k_B T$

mit der Boltzmann-Konstante $k_B$. Die linken Seiten der idealen Gasgleichung und der 2. Form der kinetischen Gastheorie sind identisch, weswegen man sie gleichsetzen kann. Nach Umstellen ergibt sich die 3. Form der kinetischen Gastheorie, die nun die Zustandsgröße Temperatur $T$ durch die Bewegungsenergie der Teilchen ausdrückt.

$ \overline{E_{kin}}=\frac32 k_B T$

Hier zeigt sich erneut eine der Grundannahmen der Gastheorie, wonach sich die Teilchen eines Stoffes schneller bewegen, je wärmer der Stoff ist.