Die Sonne
Sonne und Sonnensystem; Zustandsgrößen der Sonne; Sonnenatmosphäre; Innerer Aufbau der Sonne; Aufgaben zur Sonne
Inhaltsverzeichnis zum Thema
- Rolle der Sonne für das Leben auf der Erde
- Aufbau der Sonne
- Sonnenphänomene in der Sonnenatmosphäre
- Granulation
- Protuberanzen
- Sonnenflecken
Rolle der Sonne für das Leben auf der Erde
Die Sonne ist ein Stern unter den vielen weiteren Sternen am Nachthimmel. Die Sonne steht im Zentrum des Sonnensystems und ist auch dessen Namensgeber. Die Sonne ist für das Leben auf der Erde von entscheidender Bedeutung. Ohne das Licht und die Wärme der Sonne hätte sich auf unserem Planeten kein Leben entwickeln können. Dabei ist natürlich auch der Abstand von der Sonne wichtig: Wäre dieser zu gering, wäre es zu heiß. Wäre er zu groß, wäre es zu kalt.
Neben dem Abstand ist natürlich auch die Rate wichtig, mit der die Sonne ihre Energie abstrahlt. Diese unterliegt Schwankungen und ist neben Vulkanausbrüchen der Hauptgrund für Wärmeperioden und Eiszeiten. Gerade jetzt steigt die Effektivität der Sonne immer weiter an wie zuletzt in der mittelalterlichen Warmzeit. In dieser konnte man sogar in Schottland Wein anbauen. Aber nicht nur für die Temperaturen auf der Erde ist die Sonne von Bedeutung. Auch für den Wind und den Regen sorgt die Sonne. Für Wind sorgt sie, indem sie die Luft nur einseitig auf der Erde erwärmt. Dadurch verringert sich auf dieser Seite der Erde die Dichte der Luft, um die Dichten wieder ins Gleichgewicht zu bringen strömt Luft von außen in dieses Gebiet, das Resultat ist Wind. Den Regen verursacht die Sonne, indem sie in großen Mengen Wasser verdampft, welches dann Wolken bildet, die später für den Niederschlag sorgen. Damit ist die Sonne der Motor für das Wetter auf der Erde. Meteorologen beobachten daher auch das Verhalten der Sonne, um mit Modellen Vorhersagen für das Wetter auf der Erde zu bestimmen.
Aufbau der Sonne
Die Sonne erscheint uns von außen wie ein 700.000 km großer Feuerball. Der Aufbau der Sonne lässt sich in unterschiedliche Zonen unterteilen, ähnlich zu den Schichten der Erde. Tief im Inneren der Sonne finden wir das Zentralgebiet. Dieses wird analog zur Erde auch als Kern bezeichnet. Hier ist es ca. 60 Millionen Kelvin heiß. Die Sonne ist an diesem Ort sehr dicht und der Druck ist dort gewaltig. An den Kern grenzt die Strahlungszone. Zusammen mit dem Kern nimmt diese 90% des Volumens der Sonne ein. Innerhalb der Strahlungszone findet sich die Konvektionszone. In dieser findet ein Wärmetransport von Innen nach Außen statt. An diese Schicht schließt sich dann die Photosphäre an. Dies ist die erste sichtbare Schicht der Sonne. Sie besitzt wegen der hohen Masse der Sonne eine nach außen hin scharfe Grenze. An die Photosphäre schließt sich dann die Korona an. Diese ist nur bei einer Sonnenfinsternis von der Erde aus sichtbar.

Sonnenphänomene in der Sonnenatmosphäre
Bei der Beobachtung der Sonne gilt ein wichtiger Grundsatz:
Auf keinen Fall direkt in die Sonne schauen, egal ob mit Hilfsmitteln oder ohne!
Ein relativ gefahrloser Weg die Sonne zu betrachten ist es, die Sonne durch ein Teleskop auf ein Blatt Papier zu projizieren und dann die vergrößerte Projektion der Sonne auf dem Papier zu betrachten. Auf diesem Wege kannst du dann in der Sonnenatmosphäre die folgenden Phänomene erkennen.
Granulation
Die körnige Oberfläche der Sonne wird als Granulation bezeichnet. Diese entsteht durch den stetigen Wärmetransport vom Inneren der Sonne nach außen. Dabei sind immer helle Flächen mit einem Durchmesser mehrerer 100 km von dunklen Umrandungslinien umgeben.
Protuberanzen
Ein weiterer Effekt auf der Sonne sind Protuberanzen. Bei diesen wird heißes Protoplasma durch magnetische Wechselwirkungen ins All hinaus geschleudert. Dadurch kühlt sich die Sonnenoberfläche darunter ab. Eine solche Stelle wird als Dunkler Fleck auf der Sonne sichtbar.

Sonnenflecken
Die Sonnenflecken haben eine Ausdehnung, die häufig größer als die der Erde ist. Sie sind ein Zeichen für die Sonnenaktivität. Je mehr Flecken die Sonne besitzt, desto höher ist ihre Strahlungsleistung. Die Flecken werden insbesondere im Rahmen des Klimawandels und der Wetterprognosen beobachtet.

Zustandsgrößen der Sonne
Die Zustandsgrößen der Sonne beschreiben den Zustand der Sonne in Zahlen. Die Sonne besitzt eine gewaltige Masse. Etwa 99,86% der Masse des gesamten Sonnensystems besitzt die Sonne: etwa $m_S=1,9884 \cdot 10^{30} \text{kg}$. Sie bildet eine relativ perfekte Kugel mit einem Durchmesser $d$ von
$d_S=1,4 \cdot 10^9 \text{m}$.
Durch Fusionsprozesse gewinnt sie gewaltige Energie. Genug, um die komplette Sonnenoberfläche auf ca. $6000°\text{C}$ zu erwärmen. Mit einer Farbtemperatur von $5800 \text{K}$ gehört sie zur Spektralklasse G2V. Damit ist sie ein Hauptreihenstern.
Die Sonne. Ein Stern von vielen.
Allein in der Milchstraße, die nur eine von vielen Galaxien im Universum ist, gibt es ca. 200 bis 300 Milliarden Sterne. Damit ist die Sonne nur einer von vielen Sternen im Universum. Viele sind größer oder kleiner als die Sonne und auch die Farbe der Sterne unterscheidet sich. Daher hat man versucht, die Sterne in Klassen einzuteilen. Da gibt es die Hauptreihensterne, wie die Sonne einer ist. Zu dieser Reihe gehören alle Zwerge außer die weißen Zwerge. Daher bezeichnet man die Sterne der Hauptreihe in der astronomischen Alltagssprache auch als Zwerge. Daneben gibt es aber auch noch Riesen und Überriesen, welche entweder gelb oder rötlich leuchten. Alle diese Sterne hat man versucht, im sogenannten Hertzsprung-Russell-Diagramm einzuordnen.
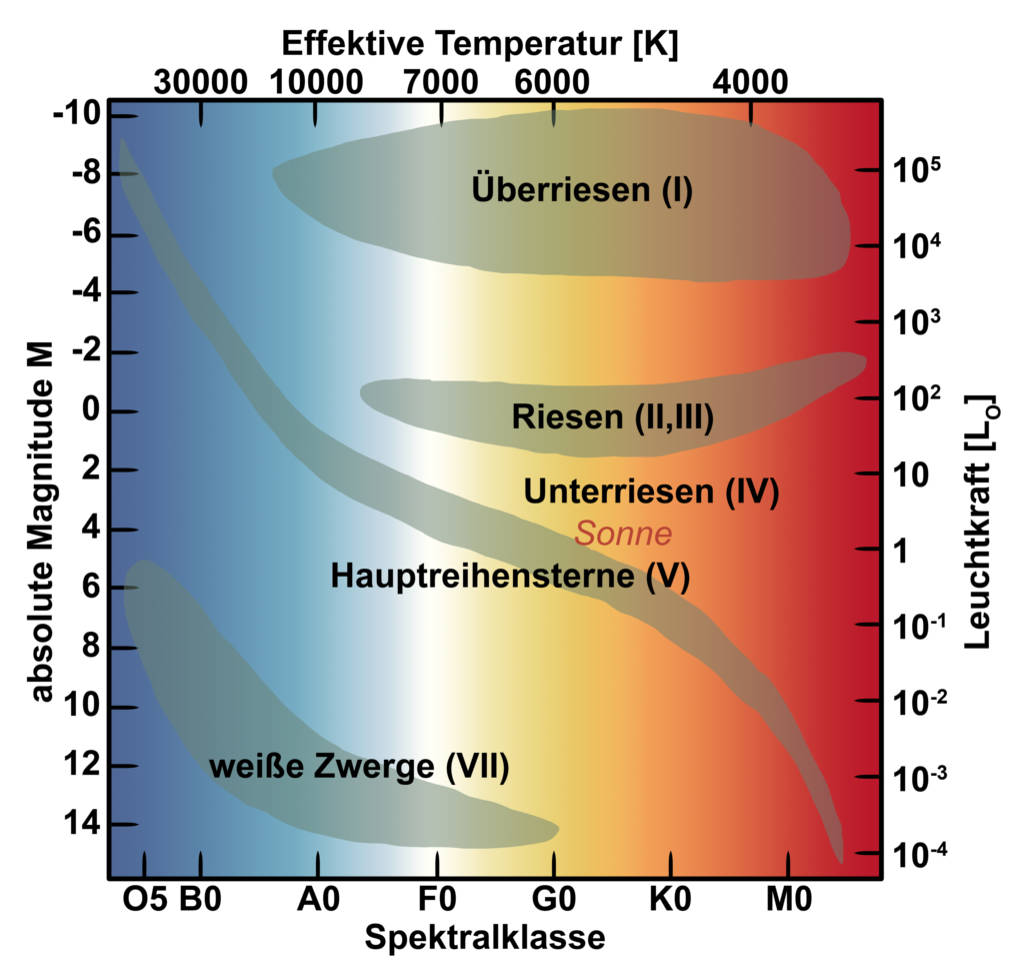
Lebenszyklus der Sterne
Auch der Lebenszyklus dieser Sterne unterscheidet sich, je nachdem wie viel Masse die Sterne besitzen.
- Haben die Sterne weniger als 60% der Masse der Sonne, werden sie direkt zu einem roten Zwerg, sobald sie keinen Wasserstoff mehr für die Fusion haben.
- Haben die Sterne mehr als 60% der Sonnenmasse aber weniger als 144% der Sonnenmasse, beginnt zunächst das He-Brennen des Sterns. Dabei dehnt sich die Hülle des Sterns gewaltig aus. Der Stern wird zum Roten Riesen und stößt schließlich seine Hülle ab, wenn auch das He-Brennen abbricht. Zurück bleibt ein weißer Zwerg mit einem planetaren Nebel, der vormals seine Gashülle war. Dies ist auch das Schicksal der Sonne.
- Besitzt der Stern eine Masse, die größer als 144% der Masse der Sonne ist, kommt es nach dem He-Brennen zum Gravitationskollaps und zu einer Supernova, das heißt einer gewaltigen Explosion, bei der die Gashülle weit hinaus ins Universum verteilt wird. Zurück bleibt ein Neutronenstern. Dieser hat eine extrem hohe Dichte und konzentriert die komplette Masse des vormaligen Sterns.
- Ist die Masse des Sterns größer als 300% der Sonnenmasse, bildet sich nach der Supernova kein stabiler Neutronenstern. Da die konzentrierte Masse so groß und konzentriert vorliegt, bildet sich an diesem Punkt ein schwarzes Loch aus.
Alle Lerntexte zum Thema
Lerntexte zum Thema
Die Sonne (1 Lerntext)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Die Sonne (1 Arbeitsblatt)
Beliebteste Themen in Physik
- Temperatur
- Schallgeschwindigkeit
- Dichte
- Drehmoment
- Transistor
- Lichtgeschwindigkeit
- Elektrische Schaltungen – Übungen
- Galileo Galilei
- Rollen- Und Flaschenzüge Physik
- Radioaktivität
- Aufgaben zur Durchschnittsgeschwindigkeit
- Lorentzkraft
- Beschleunigung
- Gravitation
- Ebbe und Flut
- Hookesches Gesetz Und Federkraft
- Elektrische Stromstärke
- Elektrischer Strom Wirkung
- Reihenschaltung
- Ohmsches Gesetz
- Freier Fall
- Kernkraftwerk
- Reflexionsgesetz: Ebener Spiegel – Übungen
- Was sind Atome
- Aggregatzustände
- Infrarot, Uv-Strahlung, Infrarot Uv Unterschied
- Isotope, Nuklide, Kernkräfte
- Transformator
- Lichtjahr
- Si-Einheiten
- Fata Morgana
- Gammastrahlung, Alphastrahlung, Betastrahlung
- Kohärenz Physik
- Mechanische Arbeit
- Schall
- Elektrische Leistung
- Dichte Luft
- Ottomotor Aufbau
- Kernfusion
- Trägheitsmoment
- Heliozentrisches Weltbild
- Energieerhaltungssatz Fadenpendel
- Linsen Physik
- Ortsfaktor
- Interferenz
- Diode und Photodiode
- Wärmeströmung (Konvektion)
- Schwarzes Loch
- Frequenz Wellenlänge
- Elektrische Energie




 Sonnenatmosphäre
Sonnenatmosphäre









