Rechnen in der Elektrik
Elektrische Geräte prägen unseren Alltag, doch was sind diese Kennwerte auf dem Gerät?
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Grundlagen
- Ohm’sches Gesetz
- Widerstandsgesetz
- Elektrische Arbeit und elektrische Leistung
- Kirchhoff’sche Gesetze für den ohm'schen Widerstand
- Reihenschaltung
- Parallelschaltung
- Schaltungskombinationen
Grundlagen
Du kennst bereits die elektrische Stromstärke $I$ mit ihrer Einheit „Ampere“ $1 A$ und auch die elektrische Spannung $U$ mit ihrer Einheit „Volt“ $1 V$, vielleicht kennst du auch schon den elektrischen Widerstand $R$ mit seiner Einheit „Ohm“ $1 \Omega$. Dann hast du sehr gute Vorkenntnisse, um mit dem Rechnen in der Elektrik zu starten.
Ohm’sches Gesetz
Die drei Größen Stromstärke, Spannung und Widerstand sind bei konstanter Temperatur und Gleichstrom über das Ohm’sche Gesetz verknüpft. Da der Widerstand bestimmt, wie groß die Spannung sein muss, um einen bestimmten elektrischen Strom zu ermöglichen, gilt für seine Einheit und das Ohm’sche Gesetz:
$[R] = 1 \Omega = \frac{1 V}{1 A}~~$ und $~~R=\frac{U}{I}$.
Dieses lässt sich aber auch über den Dreisatz umformen zu:
$U = R \cdot I~~$ und $~~I=\frac{U}{R}$.
Dafür gibt es gleich zwei Merkhilfen:
- „$URI$“: $U$ ist gleich $R$ mal $I$
- „$RUdI$“: $R$ ist $U$ $d$urch $I$
Widerstandsgesetz
Der elektrische Widerstands eines Werkstückes lässt sich über das Widerstandsgesetz bestimmen. Jedes unterschiedliche Material hat dabei einen spezifischen elektrischen Widerstand $\varrho$. Mit der Einheit $[\varrho]=1 \frac{\Omega \cdot mm^2}{m}$.
Auch die Länge des Werkstücks in Stromrichtung $l$ und dessen Querschnittsfläche $A$ spielen eine Rolle. Stell dir einen vollen Weihnachtsmarkt vor. Personengruppen würden sich hauptsächlich an Engstellen stauen, also dort, wo die Querschnittsfläche $A$ klein ist. Wenn die Engstelle besonders lang ist, also die Länge $l$ sehr groß ist, geht es ebenfalls langsamer voran. Eine kleine Querschnittsfläche und eine große Länge vergrößern also den Widerstand. So folgt das Widerstandsgesetz:
$R=\frac{\varrho \cdot l}{A}$.
Elektrische Arbeit und elektrische Leistung
Auf vielen Verbrauchern steht eine Zahl mit einem nachgestellten $\text{W}$, auf alten „Glühlampen“ häufig $60\text{W}$. Dies ist die Kennzahl für die Leistung, die das Gerät benötigt. In diesem Fall wäre die elektrische Leistung $P$ 60 Watt. Die Leistung ist das Produkt aus Stromstärke $I$ und Spannung $U$. Willst du wissen, welche Arbeit du damit verrichten kannst, kommt es darauf an, wie lange du die gezeigte Leistung erbringst. Daher ist die elektrische Arbeit $W_{el}$, das Produkt aus Leistung $P$ und Zeit $t$.
$W_{el}=U \cdot I \cdot t = P \cdot t~~$ und $~~P=U \cdot I = \frac{W_{el}}{t}$
Kirchhoff’sche Gesetze für den ohm'schen Widerstand
Bei der Berechnung musst du zwischen der Parallelschaltung und der Reihenschaltung unterscheiden. Dafür gibt es die Kirchhoff'schen Gesetze.
Reihenschaltung
In einer Reihenschaltung verteilt sich die Spannung auf die verschiedenen Verbraucher. Die Stromstärke gilt jedoch unverändert für den gesamten Stromkreis. Daher wird die Größe der Widerstände in der Reihenschaltung auch direkt zu einem Gesamtwiderstand addiert.
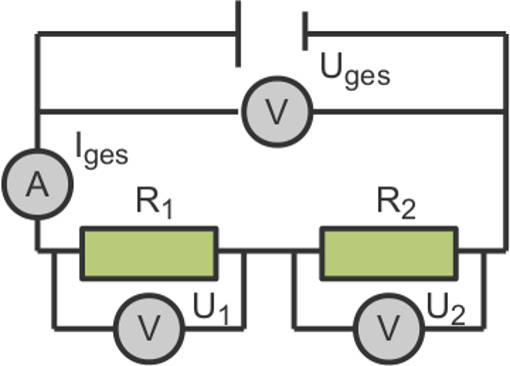
$I_{ges}=I_1=I_2$, $~~~~U_{ges}=U_1 + U_2~~$ und $~~R_{ges}=R_1 + R_2$
Parallelschaltung
Bei der Parallelschaltung teilt sich die Stromstärke auf die Verbraucher auf, die Spannung bleibt konstant. Um dieses beim Addieren zu berücksichtigen, werden die Kehrwerte der Teilwiderstände addiert. Die Summe ist dann der Kehrwert des Gesamtwiderstandes. Alternativ lässt sich bei nur zwei Teilwiderständen auch das Produkt der Teilwiderstände durch ihre Summe teilen. Dies funktioniert aber wirklich nur bei zwei Widerständen.
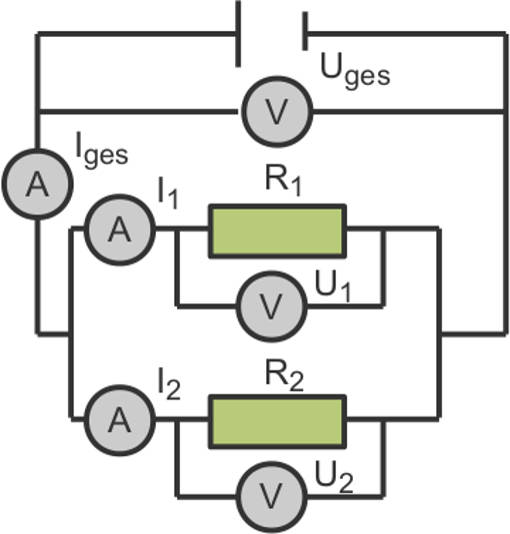
$I_{ges}=I_1+I_2$, $~~~~U_{ges}=U_1 = U_2$, $~~~~\frac{1}{R_{ges}}=\frac{1}{R_1} + \frac{1}{R_2}~~$ und $~~R_{ges}=\frac{R_1 \cdot R_2}{R_1 + R_2}$
Schaltungskombinationen
Es gibt auch Kombinationen von Schaltungen. Bei diesen wird immer von Innen nach Außen gerechnet. Ziel ist es, die Widerstände so in Gruppen zusammenzufassen, dass du die Rechnung vereinfachen kannst. Schau dir dazu einmal dieses Beispiel an.
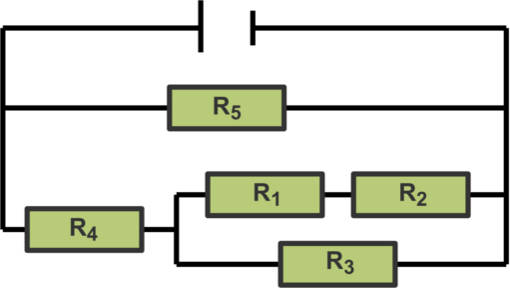
Um den Gesamtwiderstand zu bestimmen, müssen wir zunächst die Widerstände $R_1$ und $R_2$ addieren.
$R_{1,2}=R_1+R_2$
Dann müssen wir den Kehrwert des Widerstandes $R_{1,2}$ und $R_3$ addieren.
$\dfrac{1}{R_{1,2,3}}=\dfrac{1}{R_1+R_2}+\dfrac{1}{R_3}$
Zu dem neuen Widerstand $R_{1,2,3}$ addieren wir dann den Widerstand $R_4$. Dann können wir zum Kehrwert dieses Widerstandes wiederum den Kehrwert des Widerstandes $R_5$ addieren und erhalten als Summe den Kehrwert des Gesamtwiderstandes $R_{ges}$.
$\dfrac{1}{R_{ges}}=\dfrac{1}{R_5}+\dfrac{1}{R_4+R_{1,2,3}}$
Alle Videos und Lerntexte zum Thema
Videos und Lerntexte zum Thema
Rechnen in der Elektrik (2 Videos, 1 Lerntext)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Rechnen in der Elektrik (2 Arbeitsblätter)
Beliebteste Themen in Physik
- Temperatur
- Schallgeschwindigkeit
- Dichte
- Drehmoment
- Transistor
- Lichtgeschwindigkeit
- Elektrische Schaltungen – Übungen
- Galileo Galilei
- Rollen- Und Flaschenzüge Physik
- Radioaktivität
- Aufgaben zur Durchschnittsgeschwindigkeit
- Lorentzkraft
- Beschleunigung
- Gravitation
- Ebbe und Flut
- Hookesches Gesetz Und Federkraft
- Elektrische Stromstärke
- Elektrischer Strom Wirkung
- Reihenschaltung
- Ohmsches Gesetz
- Freier Fall
- Kernkraftwerk
- Reflexionsgesetz: Ebener Spiegel – Übungen
- Was sind Atome
- Aggregatzustände
- Infrarot, Uv-Strahlung, Infrarot Uv Unterschied
- Isotope, Nuklide, Kernkräfte
- Transformator
- Lichtjahr
- Si-Einheiten
- Fata Morgana
- Gammastrahlung, Alphastrahlung, Betastrahlung
- Kohärenz Physik
- Mechanische Arbeit
- Schall
- Elektrische Leistung
- Dichte Luft
- Ottomotor Aufbau
- Kernfusion
- Trägheitsmoment
- Heliozentrisches Weltbild
- Energieerhaltungssatz Fadenpendel
- Linsen Physik
- Ortsfaktor
- Interferenz
- Diode und Photodiode
- Wärmeströmung (Konvektion)
- Schwarzes Loch
- Frequenz Wellenlänge
- Elektrische Energie





 Rechnen mit dem elektrischen Widerstand
Rechnen mit dem elektrischen Widerstand
 Sachaufgaben zur Spannung
Sachaufgaben zur Spannung









