Physikalisch Rechnen
Lösung von physikalischen und mathematischen Aufgaben
Inhaltsverzeichnis zum Thema
- Einleitung
- 1. Die Aufgabe lesen und verstehen
- 2. Gesuchte und gegebene Größen und Einheiten
- Umrechnen der Einheiten
Einleitung
Auf dieser Themenseite sollst du lernen, wie du Aufgaben aus den Fächern Mathematik und Physik lösen kannst. Das Vorgehen ist in beiden Fächern ähnlich. Im Mathematikunterricht lernst du, wie du Ansätze findest und Gleichungen löst sowie wichtige Rechenregeln wie das Bruchrechnen, Funktionen und die Integral- und Differentialrechnung. Du lernst also dein mathematisches Handwerkszeug ohne konkrete Anwendung. Im Mathematikunterricht sollst du meist explizit neu erlernte Rechentechniken üben oder sie im Rahmen von Textaufgaben anwenden lernen.
Die Physik hingegen beschreibt reale Phänomene der Natur durch Mathematik. Die Mathematik ist ein Werkzeug der Physik, eine Möglichkeit die Natur zu abstrahieren und durch Formeln zu beschreiben. Somit lassen sich präzise Lösungen und Vorhersagen berechnen, die anschließend im realen Experiment überprüft werden. Du kannst keine Physik machen, ohne Mathematik zu beherrschen. Bei Aufgaben im Physikunterricht wendest du die Grundlagen aus dem Mathematikunterricht an. Dabei musst du meist viele Rechenregeln nacheinander anwenden. Wie du grundsätzlich die meisten Aufgaben lösen kannst, davon handelt diese Seite.
1. Die Aufgabe lesen und verstehen
Wenn du eine Textaufgabe in Mathematik oder eine Physikaufgabe gestellt bekommst, solltest du die Aufgabe zunächst aufmerksam und vollständig durchlesen. Es ist wichtig, die ganze Aufgabe zu zunächst vollständig zu lesen, da wichtige Informationen oder Hinweise zur Lösungen früher Teilaufgaben manchmal erst bei späteren Teilaufgaben eingeführt werden. Unabhängig davon ist es nie verkehrt zu wissen, was dich erwartet.
Nach dem Lesen der Aufgabe solltest du die Aufgabenstellung in jedem Fall verstanden haben. Nichts ist ärgerlicher, als eine Formel richtig gefunden oder gelöst zu haben, die gar nicht gesucht war. Solltest du Schwierigkeiten haben, eine Aufgabe zu verstehen, lies sie noch einmal, aber lasse dabei angegebene Zahlen und unnötige Informationen weg. Dies kann helfen, den Kern der Aufgabe verständlicher zu machen.
2. Gesuchte und gegebene Größen und Einheiten
Als nächstes ist es wichtig, dass du dir alle gegebenen und gesuchten Größen klarmachst. Es hat sich bewährt, die gegebenen Größen einfach herauszuschreiben. Meist gibt es mehrere gegebenen Größen, die entweder explizit im Text angegeben sind oder im Falle von Naturkonstanten sowieso bekannt sind. Gesucht ist pro Teilaufgabe meist nur eine Größe. Wenn es dir hilft, kannst du auch ein Farbsystem verwenden.
Wenn du dir die Größen notierst, schreibe auch immer gleich das Formelzeichen dazu. Notiere dir statt $5\,$N lieber $F=5\,$N. Manchmal sind auch mehrere Größen mit gleichem Formelzeichen gegeben, beispielsweise zwei Massen. Stelle sicher, dass du sie unterschiedlich notierst. Hierfür eignet sich beispielsweise ein Index wie $m_1=17,3\,$kg und $m_2=512\,$g. Statt einer Zahl kannst du auch einen Begriff im Index verwenden. Grundsätzlich gilt: Es ist egal wie du deine Größen indizierst, solange du weißt, was gemeint ist. Falls verschiedene Größen bereits mit Index gegeben sind, bietet es sich an, diesen zu übernehmen, um Verwechslungen zu vermeiden.
Wie du oben gesehen hast, sind auch die Einheiten stets zu notieren, da sie unterschiedlich sein können. Vor Lösen der Aufgabe solltest du die Einheiten in SI-Einheiten umrechnen. Im obigen Beispiel ist also $m_2=512\,\text{g}=0,512\,$kg.
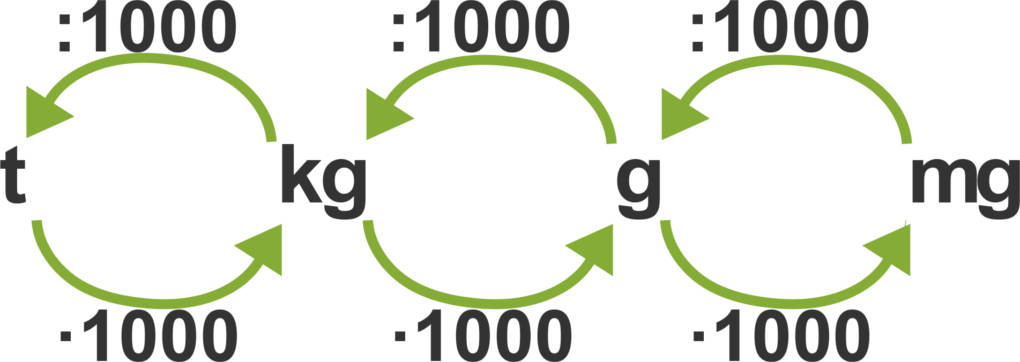
Umrechnen der Einheiten
Einheiten können mit sogenannten Dezimalpräfixen versehen werden, wenn ein dezimales Vielfaches oder ein dezimaler Bruchteil der Einheit gemeint ist. Gängige Präfixe für Vielfache sind Kilo (k), Mega (M), Giga (G) und Terra (T) und stehen für das $10^{3}$-fache, $10^{6}$-fache, $10^{9}$-fache und $10^{12}$-fache einer Einheit. Beispiele sind:
$10.000\,\text{g}=10\,\text{kg} \text{ oder } 3,6\,\text{MJ}=3.600.000\,\text{J} $
$ \text{ oder } 14,77\,\text{TeV}=14.770.000.000.000\,\text{eV} $
Gängige Präfixe für Bruchteile sind Milli (m), Mikro ($\mu$) oder Nano (n) und stehen für das $10^{-3}$-fache, $10^{-6}$-fache und $10^{-9}$-fache einer Einheit. Beispiele sind:
$36\,\text{mg}=0,000036\,\text{kg} \text{ oder } 5,6\,\mu\text{m}=0,0000056\,\text{m} $.
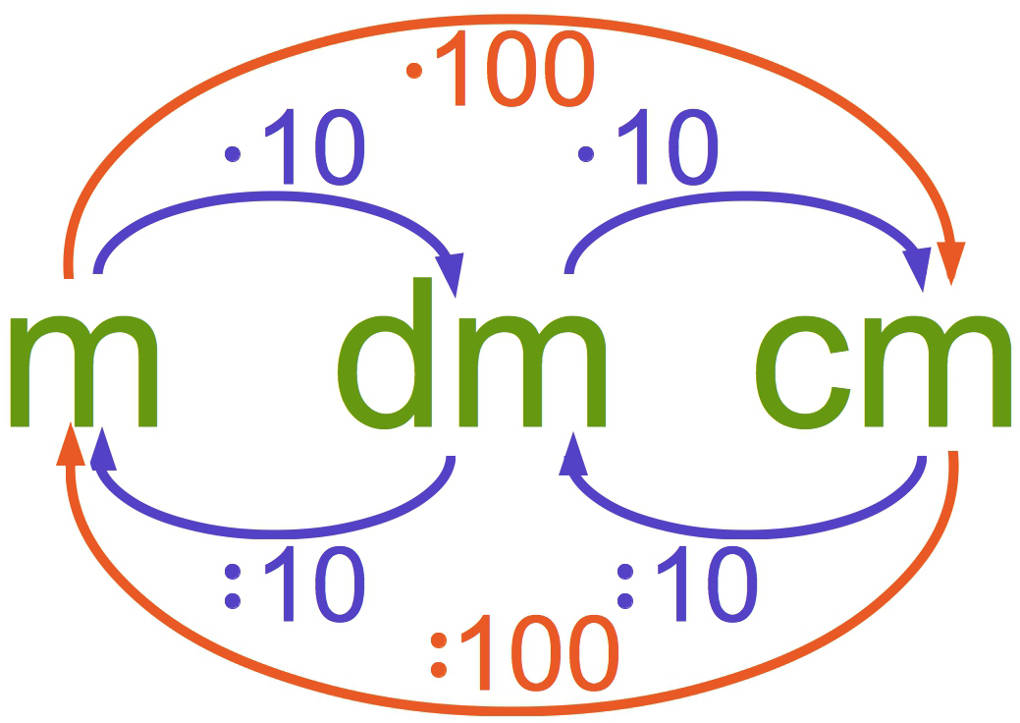
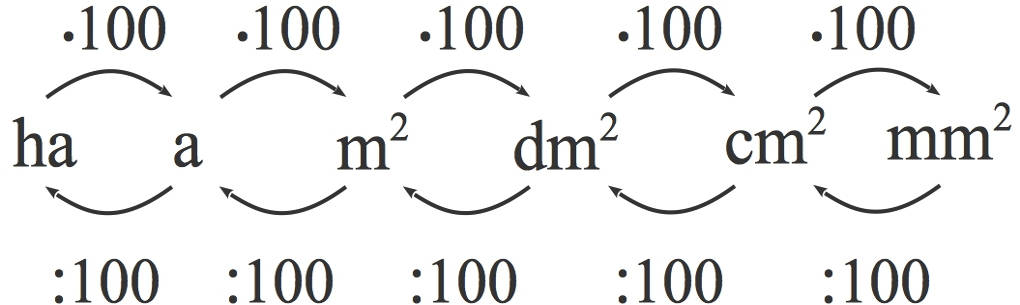
Die SI-Einheiten sind ohne Präfix angegeben. Die einzige Ausnahme bildet die Einheit der Masse, die standardmäßig Kilogramm ist. Um Einheiten umzurechnen, musst lediglich mit dem Zahlenwert, der dem Präfix entspricht, multiplizieren oder dividieren. Falls du dir unsicher bist, ob du multiplizieren oder dividieren musst, kannst du dir folgende Faustregel merken: Soll das Präfix größer werden, muss die Zahl kleiner werden und umgekehrt. Ist eine Einheit mit einem Exponenten versehen (z.B. m² für Flächen, m/s² bei der Beschleunigung), so muss auch das Präfix potenziert werden.
3. Formeln finden und lösen
Hast du dir alle gesuchten und gegebenen Größen herausgeschrieben und die Einheiten angeglichen, geht es nun ans Lösen der Aufgabe. Dafür benötigst du normalerweise Formeln. Die nötigen Formeln kannst du entweder aus deinen Notizen oder aus Formelsammlungen herausschreiben. Meist brauchst du auch Formeln, die du bereits vor Wochen, Monaten oder in vergangenen Schuljahren gelernt hast, also versuche sie nicht zu vergessen. Physik baut aufeinander auf. Achte darauf, dass es oftmals mehrere Formeln gibt, die dasselbe beschreiben. Beispielsweise unterscheiden sich die Formeln zur Berechnung eines elektrischen Feldes, je nachdem, um was es geht. Eine Punktladung hat ein anderes elektrisches Feld als ein Plattenkondensator, dieser wiederum unterschiedet sich vom Zylinderkondensator. Daher ist auch der eingangs erwähnte Punkt wichtig, die Aufgabenstellung zu verstehen.
Zum Lösen der Aufgabe musst du nun die Formeln identifizieren, die alle gegebenen und gesuchten Größen oder manche dieser beinhalten. Nun liegt es an dir, alle unbekannten Variablen zu eliminieren. Dabei machst du dir deine mathematischen Grundlagen zunutze: das Gleichsetzen oder Einsetzen von Gleichungen sowie Äquivalenzumformung. Hast du es geschafft, dass eine Formel die gegebene Größe enthält und alle anderen Variablen bekannt sind, folgt der letzte Schritt.
4. Einsetzen der Zahlenwerte
Erst ganz zum Schluss setzt du die anfangs herausgeschriebenen Zahlenwerte ein. Achte dabei auf die richtigen Einheiten und darauf, dass auch Einheiten sich kürzen oder potenzieren können. Du kannst mit Einheiten prinzipiell wie mit Variablen rechnen. Falls das Eingabefeld im Taschenrechner nicht groß genug sein sollte, die ganze Formel mit Zahlenwerten als Ganzes einzutippen, speichere deine Zwischenergebnisse im Taschenrechner und rechne mit Ihnen weiter. Rechne bestenfalls niemals mit gerundeten Zahlen weiter, sonst wird das Ergebnis ungenau. Erst das Endergebnis kann gegebenenfalls gerundet werden. Überprüfe in jedem Fall, ob die Einheit passt. Wenn du beispielsweise eine Kraft berechnest, muss stets die Einheit Newton herauskommen. Die Einheit ist ein guter Indikator dafür, ob du richtig gerechnet hast. So kannst du dich selbst überprüfen.

Alle Lerntexte zum Thema
Lerntexte zum Thema
Physikalisch Rechnen (1 Lerntext)
Beliebteste Themen in Physik
- Temperatur
- Schallgeschwindigkeit
- Dichte
- Drehmoment
- Transistor
- Lichtgeschwindigkeit
- Elektrische Schaltungen – Übungen
- Galileo Galilei
- Rollen- Und Flaschenzüge Physik
- Radioaktivität
- Aufgaben zur Durchschnittsgeschwindigkeit
- Lorentzkraft
- Beschleunigung
- Gravitation
- Ebbe und Flut
- Hookesches Gesetz Und Federkraft
- Elektrische Stromstärke
- Elektrischer Strom Wirkung
- Reihenschaltung
- Ohmsches Gesetz
- Freier Fall
- Kernkraftwerk
- Reflexionsgesetz: Ebener Spiegel – Übungen
- Was sind Atome
- Aggregatzustände
- Infrarot, Uv-Strahlung, Infrarot Uv Unterschied
- Isotope, Nuklide, Kernkräfte
- Transformator
- Lichtjahr
- Si-Einheiten
- Fata Morgana
- Gammastrahlung, Alphastrahlung, Betastrahlung
- Kohärenz Physik
- Mechanische Arbeit
- Schall
- Elektrische Leistung
- Dichte Luft
- Ottomotor Aufbau
- Kernfusion
- Trägheitsmoment
- Heliozentrisches Weltbild
- Energieerhaltungssatz Fadenpendel
- Linsen Physik
- Ortsfaktor
- Interferenz
- Diode und Photodiode
- Wärmeströmung (Konvektion)
- Schwarzes Loch
- Frequenz Wellenlänge
- Elektrische Energie












