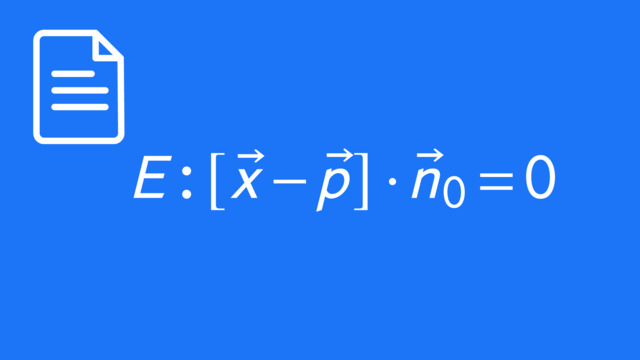Parameterform einer Ebene


in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
Grundlagen zum Thema Parameterform einer Ebene
Nach dem Schauen dieses Videos wirst du in der Lage sein, die Parametergleichung von Ebenen aufzustellen.
Zunächst lernst du, wie die Ebenengleichung in Parameterform aufgebaut ist. Anschließend siehst du, wie wir die Parametergleichung einer Ebene aufstellen können, wenn wir drei Punkte der Ebene gegeben haben. Abschließend erfährst du, dass die Parametergleichung einer Ebene nicht eindeutig bestimmt ist.

Das Video beinhaltet Schlüsselbegriffe, Bezeichnungen und Fachbegriffe wie Ebene, Parameterform, Koordinatenform, Normalenform, Stützvektor, Richtungsvektor und Parameter.
Bevor du dieses Video schaust, solltest du bereits die Parametergleichung einer Geraden kennen. Außerdem solltest du grundlegendes Wissen zur Vektorrechnung haben.
Nach diesem Video wirst du darauf vorbereitet sein, die Koordinaten- und Normalenform von Ebenengleichungen kennenzulernen.
Transkript Parameterform einer Ebene
Räumliches Denken ist so 'ne Sache. Manche haben Schwierigkeiten beim Einparken, andere können rechts und links nur schwer auseinander halten, aber WIR geben es uns heute mal so richtig und betrachten "die Paramaterform der Ebene". Wenn wir eine Ebene im dreidimensionalen Raum betrachten, kann die zugehörige EbenenGLEICHUNG in drei verschiedenen Formen vorliegen: Parameter-, Normalen- oder Koordinatenform. In diesem Video beschäftigen wir uns erstmal mit der Parameterform. Die grundlegende Idee der Parameterform solltest du auch schon kennen. Denn die ist prinzipiell dieselbe wie bei der Parameterform einer GERADEN. Eine Gerade in Parameterform ist ja so aufgebaut, dass wir erstens einen "Stützvektor" haben,. der vom Ursprung zu einem beliebigen Punkt "A" der Gerade verläuft, und dass wir zweitens einen "Richtungsvektor" haben, der die Richtung der Geraden vorgibt und durch den wir mit skalarer Multiplikation jeden Punkt der Gerade erreichen können. Diese beiden Vektortypen sind auch Bestandteil einer EBENENgleichung in Parameterform, nur, dass wir jetzt einen ZWEITEN Richtungsvektor mit Parameter hinzunehmen. Dieser zweite Richtungsvektor muss eine Bedingung erfüllen: Er muss linear unabhängig vom ersten Richtungsvektor sein. Die beiden Vektoren dürfen also nicht kollinear sein, sprich parallel verlaufen. Denn DANN erreichen wir mit dem zweiten Richtungsvektor auch Punkte "seitlich" der Geraden . Die beiden Richtungsvektoren definieren zusammen mit dem Stützvektor eine Ebene im Raum. Mit den Parametern r und s können wir die Richtungsvektoren so multiplizieren, dass wir jeden erdenklichen Punkt der Ebene als Linearkombination des Stützvektors und der beiden Richtungsvektoren darstellen können. Den Punkt P der Ebene können wir zum Beispiel erreichen, indem wir den ersten Richtungsvektor mit zwei und den zweiten mit "minus eins" multiplizieren. Die Richtungsvektoren "spannen" eine Ebene auf, weshalb sie manchmal auch "Spannvektoren" genannt werden. Dafür müssen sie erstens, wie bereits erwähnt, linear unabhängig sein und zweitens darf es sich bei keinem der beiden Vektoren um den "Nullvektor" handeln. Denn dieser hat ja überhaupt keine RICHTUNG, was unsere Ebene wieder zu einer Gerade degradieren würde. Wir brauchen also zwei linear unabhängige Vektoren ungleich dem Nullvektor, damit diese die Ebene tatsächlich "aufspannen" können. Alles klar, am besten schauen wir uns die Theorie mal an einem Rechenbeispiel an! Wir haben drei Punkte gegeben und sollen erstens feststellen, ob diese Punkte tatsächlich eine Ebene aufspannen und zweitens diese Ebene gegebenenfalls dann auch in Parameterform angeben. Wir legen mal los! Wir schnappen uns zunächst Punkt A und übernehmen seine Koordinaten für unseren Stützvektor. An dieser Stelle könnten wir auch die Koordinaten von Punkt B oder C für unseren Stützvektor wählen. Für die Frage, ob diese drei Punkte zusammen eine Ebene aufspannen, und wie diese Ebene im Raum liegt, macht das grundsätzlich keinen Unterschied. Wir haben aber Punkt A gewählt und bilden als nächstes die Richtungsvektoren "AB" (wir berechnen dafür wie immer "Endpunkt minus Anfangspunkt") und "AC". Diese beiden Richtungsvektoren sind jetzt entscheidend, denn damit eine Ebene aufgespannt werden kann, müssen sie erstens ungleich dem Nullvektor sein (das ist offensichtlich der Fall) und zweitens dürfen sie nicht kollinear sein. Das überprüfen wir, indem wir ein "Skalar t" als Faktor suchen, mit dem wir Vektor "AC" aus Vektor "AB" erzeugen können. Aber auch hierzu ist schnell ersichtlich, dass wir kein passendes "t" für alle drei Zeilen gleichzeitig finden, "AC" also kein Vielfaches von "AB" ist. Die beiden Vektoren sind nicht kollinear und die Punkte A, B und C spannen somit eine Ebene auf. Die Parameterform der Ebene aufzustellen, ist jetzt auch schnell erledigt. "Stützvektor plus Parameter r mal ersten Richtungsvektor plus Parameter s mal zweiten Richtungsvektor." Fertig! Mit dieser Ebenengleichung können wir für jeden beliebigen Punkt groß-X der Ebene den Ortsvektor x darstellen, wenn wir passende Werte für die Parameter r und s wählen. Wie eben schon angeklungen ist, ist die Parametergleichung einer Ebene nicht eindeutig bestimmt. Als Stützvektor können wir jeden Vektor wählen, der den Ursprung mit einem Punkt der Ebene verbindet, und als Richtungsvektoren kommen auch zwei beliebige in Frage, solange sie nicht den Nullvektor enthalten, nicht kollinear sind und die Vektorpfeile sich in die entsprechende Ebene legen lassen. In dieser Aufgabe hätten wir also zum Beispiel auch Punkt B als Stützvektor wählen können. Wir erhalten dann auch andere Koordinaten für die Richtungsvektoren und die Parametergleichung der Ebene sieht anders aus. An der Ebene, die durch diese Gleichung definiert wird, ändert das aber nichts! Tja, auch im Schulfach Mathematik gibt es eben manchmal Raum für ein bisschen "künstlerische Freiheit". Bevor du dich da austoben kannst, fassen wir nochmal schnell das Wichtigste zusammen. Eine Ebene im Raum kann durch eine Ebenengleichung in PARAMETERFORM angegeben werden. In dieser Form setzt sich die Gleichung aus einem Stützvektor und zwei Richtungsvektoren zusammen, die manchmal auch Spannvektoren genannt werden, und die jeweils noch mit einem Parameter multipliziert werden. Für jedes Wertepaar der Parameter r und s erhalten wir so den Ortsvektor x eines Punktes groß-X, der in der Ebene liegt. Eine Parametergleichungen von einer Ebene aufzustellen, ist Gewöhnungssache! Aber mit ein bisschen Übung beherrschen wir Ebenen im Raum dann spielend!
Parameterform einer Ebene Übung
-
Bestimme die Stütz- und Richtungsvektoren.
TippsDas Bild zeigt dir den Stützvektor (grün) und die Richtungsvektoren (blau und rot). Überlege, welche Besonderheit die Vektoren haben.
Bei dieser Ebenengleichung sind der Stützvektor grün und die Richtungsvektoren blau markiert. Untersuche die hier angegebene Gleichung nach Ähnlichkeiten zu unseren Ebenengleichungen.
$E:\vec{x}~=~\color{#669900} {\begin{pmatrix} {-}1 \\0\\ 0 \end{pmatrix}}\color{black}{~+~r~\cdot~}\color{lightskyblue}{\begin{pmatrix} 2 \\ 1 \\ 0 \end{pmatrix}}\color{black}{~+~s~\cdot~}\color{lightskyblue}{\begin{pmatrix} {-}3 \\ 0 \\ 1 \end{pmatrix}}\color{black}{\qquad(r, s \in \mathbb{R})}$
LösungIn dieser Aufgabe geht es um den Aufbau der Parameterform einer Ebene. Im Allgemeinen beschreibt man ihn folgendermaßen:
$E:{\vec{x}=\color{#669900} {\begin{pmatrix} a_1 \\a_2\\ a_3 \end{pmatrix}}\color{black}{~+~r~\cdot}\color{lightskyblue}{\begin{pmatrix} u_1 \\ u_2 \\ u_3 \end{pmatrix}}\color{black}{~+~s~\cdot}\color{lightskyblue}{\begin{pmatrix} v_1 \\ v_2 \\ v_3 \end{pmatrix}}}$
$\color{black}{\qquad(r, s \in \mathbb{R})}$
Der Stützvektor $\color{#669900}{\begin{pmatrix} a_1 \\a_2\\ a_3 \end{pmatrix}}$ verläuft immer vom Ursprung zu einem beliebigen Punkt der Ebene.
Die Richtungsvektoren $\color{lightskyblue}{\begin{pmatrix} u_1 \\ u_2 \\ u_3 \end{pmatrix}}$ und $\color{lightskyblue}{\begin{pmatrix} v_1 \\ v_2 \\ v_3 \end{pmatrix}}$ spannen die Ebene auf.
Mit den Parametern $r$ und $s$ können die Richtungsvektoren so multipliziert werden, dass jeder Punkt auf der Ebene erreicht werden kann.
Die angegebenen Ebenengleichungen enthalten folgende Stützvektoren und Richtungsvektoren:
$E:\vec{x}=\color{#669900} {\begin{pmatrix} 1 \\{-}6\\ 1 \end{pmatrix}}\color{black}{~+~r~\cdot}\color{lightskyblue}{\begin{pmatrix} 1 \\ 7 \\ {-}1 \end{pmatrix}}\color{black}{~+~s~\cdot}\color{lightskyblue}{\begin{pmatrix} {-}1 \\ 3 \\ 5 \end{pmatrix}}$
$\color{black}{\qquad(r, s \in \mathbb{R})}$
$E:\vec{x}=\color{#669900} {\begin{pmatrix} 2 \\1\\ 0 \end{pmatrix}}\color{black}{~+~r~\cdot}\color{lightskyblue}{\begin{pmatrix} {-}1 \\ {-}7 \\ 1 \end{pmatrix}}\color{black}{~+~s~\cdot}\color{lightskyblue}{\begin{pmatrix} {-}2 \\ {-}4 \\ 6 \end{pmatrix}}$
$\color{black}{\qquad(r, s \in \mathbb{R})}$
-
Beschreibe das Vorgehen zum Aufstellen einer Ebenengleichung in Parameterform.
TippsZuerst wird ein Punkt auf der Ebene genutzt:
$D({-}1\vert0\vert0) \qquad E(1\vert1\vert0) \qquad F({-}4\vert0\vert1)$
$\vec{d}~=~\overrightarrow{0D}~=\begin{pmatrix}{-}1\\0\\0 \end{pmatrix}$
Anschließend werden zwei Vektoren berechnet, die die Ebene aufspannen:
$\vec{e}~=~\overrightarrow{DE}~=\begin{pmatrix}1+1\\1-0\\0- 0\end{pmatrix}~=~\begin{pmatrix}2\\1\\0 \end{pmatrix}$
Lösung1. Schritt: Einen der angegebenen Punkte als Stützvektor nutzen und die Richtungsvektoren festlegen.
$\vec{a}~=~\overrightarrow{0A}~=\begin{pmatrix}a_1\\a_2\\a_3 \end{pmatrix} \qquad \vec{u}~=~\overrightarrow{AB} \qquad \vec{v}~=~\overrightarrow{AC} $
Hier:
$\vec{a}~=~\overrightarrow{0A}~=\begin{pmatrix}1\\{-}6\\1 \end{pmatrix} \qquad \vec{u}~=~\overrightarrow{AB} \qquad \vec{v}~=~\overrightarrow{AC}$
2. Schritt: Richtungsvektoren mithilfe des gewählten Punktes und jeweils eines anderen Punktes berechnen.
$\vec{u}~=~\overrightarrow{AB}~=\begin{pmatrix}b_1-a_1\\b_2-a_2\\b_3-a_3\end{pmatrix} \quad$ und $\quad \vec{v}~=~\overrightarrow{AC}~=\begin{pmatrix}c_1-a_1\\c_2-a_2\\c_3-a_3\end{pmatrix}$
In unserem Beispiel:
$\vec{u}~=~\overrightarrow{AB}~=\begin{pmatrix}2-1\\1+6\\0- 1\end{pmatrix}~=~\begin{pmatrix}1\\7\\{-}1 \end{pmatrix}$
$\vec{v}~=~\overrightarrow{AC}~=~\begin{pmatrix}0-1\\{-}3+6\\6-1 \end{pmatrix}~=~\begin{pmatrix} {-}1\\3\\ 5 \end{pmatrix}$
3. Schritt: Prüfen, ob die Richtungsvektoren eine Ebene aufspannen (ungleich Nullvektor, nicht kollinear).
$\vec{u}~=~\overrightarrow{AB}~\neq~\begin{pmatrix}0\\0\\0\end{pmatrix}$, $~\vec{v}~=~\overrightarrow{AC}~\neq~\begin{pmatrix}0\\0\\0\end{pmatrix} \quad$ und $\quad \vec{v}~\neq~t~\cdot~\vec{u}$
Beispiel:
$\vec{u}~=~\begin{pmatrix} 1 \\7\\ {-}1 \end{pmatrix}~\neq~\begin{pmatrix} 0\\0\\ 0 \end{pmatrix} \quad$ und $\quad \vec{v}~=~\begin{pmatrix} {-}1\\3\\ 5 \end{pmatrix}~\neq~\begin{pmatrix} 0\\0\\ 0 \end{pmatrix} $
und:
$\begin{pmatrix} {-}1 \\ 3 \\ 5 \end{pmatrix}~\neq~t~\cdot~\begin{pmatrix} 1 \\ 7 \\ {-}1 \end{pmatrix}$
4. Schritt: Richtungs- und Stützvektoren einsetzen.
${E:\vec{x}~=~\vec{a}~+~r~\cdot~\vec{u}~+~s~\cdot~\vec{v}}$$(r, s \in \mathbb{R})$
Unsere Gleichung lautet:
$E:\vec{x}~=~\begin{pmatrix} 1 \\{-}6\\ 1 \end{pmatrix}~+~r~\cdot~\begin{pmatrix} 1 \\ 7 \\ {-}1 \end{pmatrix}~+~s~\cdot~\begin{pmatrix} {-}1 \\ 3 \\ 5 \end{pmatrix}$
$(r, s \in \mathbb{R})$
Hinweis: Du kannst jeden der Punkte als Stützvektor nutzen und auch für die Richtungsvektoren zwei beliebige Vektoren in der Ebene wählen, die nicht kollinear sind. Hierdurch entsteht eine andere Gleichung, welche dennoch die gleiche Ebene definiert. Setzen wir $\vec{b}$ als Stützvektor sowie $\overrightarrow{BA}$ und $\overrightarrow{BC}$ als Richtungsvektoren ein, entsteht beispielsweise folgender Lösungsweg:
1. Schritt:
$\vec{b}~=~\overrightarrow{0B}~=\begin{pmatrix}2\\1\\0 \end{pmatrix} \qquad \vec{u}~=~\overrightarrow{BA} \qquad \vec{v}~=~\overrightarrow{BC}$
2. Schritt:
$\vec{u}=\overrightarrow{BA}=\begin{pmatrix}1-2\\{-}6-1\\1-0\end{pmatrix}=\begin{pmatrix}{-}1\\{-}7\\1 \end{pmatrix} \quad$ und $\quad \vec{v}=\overrightarrow{BC}=\begin{pmatrix}0-2\\{-}3-1\\6-0\end{pmatrix}=\begin{pmatrix}{-}2\\{-}4\\6 \end{pmatrix}$
3. Schritt:
$\vec{u}=\begin{pmatrix}{-}1\\{-}7\\1 \end{pmatrix}\neq~\begin{pmatrix}0\\0\\0\end{pmatrix}$, $~\vec{v}=\begin{pmatrix}{-}2\\{-}4\\6 \end{pmatrix}\neq~\begin{pmatrix}0\\0\\0\end{pmatrix} \quad$ und $~\begin{pmatrix} {-}1 \\ {-}7 \\ 1 \end{pmatrix}~\neq~t~\cdot~\begin{pmatrix} {-}2 \\ {-}4 \\ 6 \end{pmatrix}$
4. Schritt:
$E:\vec{x}=\begin{pmatrix} 2 \\1\\ 0 \end{pmatrix}+r\cdot \begin{pmatrix} {-}1 \\ {-}7 \\ 1 \end{pmatrix}+s\cdot\begin{pmatrix} {-}2 \\ {-}4 \\ 6 \end{pmatrix}$
$(r, s \in \mathbb{R})$
-
Berechne die Richtungsvektoren.
TippsDu rechnest immer Endpunkt minus Anfangspunkt:
$\vec{u}~=~\overrightarrow{AB}~=\begin{pmatrix}b_1-a_1\\b_2-a_2\\b_3-a_3\end{pmatrix} \quad$ bzw. $\quad \vec{v}~=~\overrightarrow{AC}~=\begin{pmatrix}c_1-a_1\\c_2-a_2\\c_3-a_3\end{pmatrix}$
Wenn du bei der Berechnung eines Verbindungsvektors (Vektor, der zwei Punkte verbindet) eine negative Zahl abziehst, verändert sich die Rechenoperation wie in dem Beispiel:
$A(1\vert{-}6\vert1) \qquad B(2\vert1\vert0) \qquad C(0\vert{-}3\vert6)$
$\vec{u}=\overrightarrow{AB}=\begin{pmatrix}2-1\\1-({-}6)\\0- 1\end{pmatrix}=\begin{pmatrix}2-1\\1+6\\0-1 \end{pmatrix}=\begin{pmatrix}1\\7\\{-}1 \end{pmatrix}$
LösungZum Aufstellen einer Ebenengleichung in Parameterform werden zuerst Stütz- und Richtungsvektoren festgelegt. Das hat Tom schon erledigt. Anschließend müssen die Richtungsvektoren berechnet werden, indem die Koordinaten des Anfangspunktes von den Koordinaten des Endpunktes abgezogen werden.
Gegebene Punkte:
$A(1\vert2\vert{-}4) \qquad B(3\vert5\vert1) \qquad C(4\vert3\vert0)$
Gegebene Gleichung:
${E:\vec{x}~=~\begin{pmatrix} 1\\2\\{-}4 \end{pmatrix}+~r~\cdot~~\overrightarrow{AB}~+~s~\cdot~\overrightarrow{AC}} \qquad {(r, s \in \mathbb{R})}$
Berechnung der Richtungsvektoren:
${\vec{u}~=~\overrightarrow{AB}~=~\begin{pmatrix}b_1-a_1\\b_2-a_2\\b_3-a_3\end{pmatrix}~=\begin{pmatrix}3-1\\5-2\\1+4\end{pmatrix}~=~\begin{pmatrix}2\\3\\5 \end{pmatrix}} $
${\vec{v}~=~\overrightarrow{AC}~=~\begin{pmatrix}c_1-a_1\\c_2-a_2\\c_3-a_3\end{pmatrix}~=~\begin{pmatrix}4-1\\3-2\\0+4\end{pmatrix}~=~\begin{pmatrix} 3\\1\\4 \end{pmatrix}}$
Richtungsvektoren eingesetzt:
${E:\vec{x}~=~\begin{pmatrix} 1\\2\\{-}4 \end{pmatrix}~+~r~\cdot~\begin{pmatrix} 2\\3\\5 \end{pmatrix}~+~s~\cdot~\begin{pmatrix} 3\\1\\4 \end{pmatrix}} \qquad {(r, s \in \mathbb{R})}$
-
Prüfe, ob die Angaben eine Ebene bestimmen.
TippsZwei Angaben sind richtig und bestimmen eine Ebene.
Richtungsvektoren dürfen kein Nullvektor sein.
$\vec{u} \neq \begin{pmatrix}0\\0\\0\end{pmatrix}$, $~\vec{v} \neq \begin{pmatrix}0\\0\\0\end{pmatrix} \quad$
Richtungsvektoren dürfen nicht kollinear (linear abhängig voneinander) sein. Das Beispiel zeigt dir, wie du die lineare Abhängigkeit überprüfst:
$A(2\vert5\vert1) \qquad B(8\vert2\vert13) \qquad C(0\vert6\vert{-}3)$
$\vec{u}~=~\overrightarrow{AB}~=\begin{pmatrix}8-2\\2-5\\13-1\end{pmatrix}~=~\begin{pmatrix}6\\{-}3\\12 \end{pmatrix}$
$\vec{v}~=~\overrightarrow{AC}~=~\begin{pmatrix}0-2\\6-5\\{-}3-1 \end{pmatrix}~=~\begin{pmatrix} {-}2\\1\\{-}4 \end{pmatrix}$
$\begin{pmatrix} 6\\{-}3\\12 \end{pmatrix}~=~{-}3~\cdot~\begin{pmatrix} {-}2\\1\\{-}4 \end{pmatrix}$
Die Punkte bestimmen keine Ebene, weil die entstehenden Richtungsvektoren kollinear sind.
LösungUm herauszufinden, ob die Angaben eine Ebene definieren, überprüfen wir die Richtungsvektoren.
Diese dürfen:
a) ... kein Nullvektor sein.
Ein Nullvektor hat keine Richtung. Sobald ein Richtungsvektor ein Nullvektor ist, wird vom Stützpunkt aus nur eine Gerade definiert. Sichtbar wird dies beispielsweise beim Einsetzen des Nullvektors in die Parameterform:
$\vec{x}~=\begin{pmatrix} 5\\2\\{-}1 \end{pmatrix}~+~r~\cdot~\begin{pmatrix} {-}2\\5\\1 \end{pmatrix}~+~s~\cdot~\begin{pmatrix} 0\\0\\0 \end{pmatrix}=\begin{pmatrix} 5\\2\\{-}1 \end{pmatrix}~+~r~\cdot~\begin{pmatrix} {-}2\\5\\1 \end{pmatrix}$
$(r \in \mathbb{R})$
b) ... nicht kollinear sein.
Kollineare Richtungsvektoren verlaufen parallel zueinander. Da sie vom selben Stützpunkt $A$ ausgehen, können mit ihnen nur Punkte auf einer Geraden und nicht seitlich davon erreicht werden.
Nachfolgend siehst du die Überprüfung der verschiedenen Angaben:
1) Falsch - Die Richtungsvektoren sind Nullvektoren.
$A(1\vert1\vert1) \qquad B(1\vert1\vert1) \qquad C(1\vert1\vert1)$
$\vec{u}~=~\overrightarrow{AB}~=\begin{pmatrix}1-1\\1-1\\1- 1\end{pmatrix}~=~\begin{pmatrix}0\\0\\0 \end{pmatrix}$
$\vec{v}~=~\overrightarrow{AC}~=~\begin{pmatrix}1-1\\1-1\\1-1 \end{pmatrix}~=~\begin{pmatrix} 0\\0\\0 \end{pmatrix}$
2) Falsch - Die Richtungsvektoren sind kollinear / linear abhängig voneinander.
$A(1\vert3\vert2) \qquad B(3\vert9\vert6) \qquad C(5\vert15\vert10)$
$\vec{u}~=~\overrightarrow{AB}~=\begin{pmatrix}3-1\\9-3\\6-2\end{pmatrix}~=~\begin{pmatrix}2\\6\\4 \end{pmatrix}$
$\vec{v}~=~\overrightarrow{AC}~=~\begin{pmatrix}5-1\\15-3\\10-2 \end{pmatrix}~=~\begin{pmatrix} 4\\12\\8 \end{pmatrix}$
$\quad \Rightarrow \quad \begin{pmatrix} 2\\ 6\\ 4 \end{pmatrix}~=~0{,}5~\cdot~\begin{pmatrix} 4 \\ 12 \\ 8 \end{pmatrix}$
3) Richtig - Wenn du Punkt $A$ als Stützvektor nutzt, ergeben sich folgende Rechnungen:
$A(0\vert0\vert1) \qquad B(0\vert{-}4\vert0) \qquad C(4\vert0\vert0)$
$\vec{a}~=\begin{pmatrix} 0\\0\\1 \end{pmatrix} $
Überprüfung der Richtungsvektoren:
a) Richtungsvektoren sind ungleich dem Nullvektor:
$\vec{u}=~\overrightarrow{AB}=\begin{pmatrix} 0-0 \\{-}4-0\\ 0-1 \end{pmatrix}=~\begin{pmatrix} 0 \\{-}4\\ {-}1 \end{pmatrix}~\neq~\begin{pmatrix} 0\\0\\ 0 \end{pmatrix} $
$\vec{v}~=~\overrightarrow{AC}=\begin{pmatrix} 4-0 \\0-0\\ 0-1 \end{pmatrix}=\begin{pmatrix} 4 \\ 0 \\ {-}1 \end{pmatrix}~\neq~\begin{pmatrix} 0\\0\\ 0 \end{pmatrix} $
b) Richtungsvektoren sind nicht kollinear:
$\begin{pmatrix} 0 \\{-}4\\ {-}1 \end{pmatrix}~\neq~t~\cdot~\begin{pmatrix} 4 \\ 0 \\ {-}1 \end{pmatrix}$
Es entsteht die Ebenengleichung:
$E:\vec{x}~=~\begin{pmatrix} 0\\0\\1 \end{pmatrix}~+~r~\cdot~\begin{pmatrix} 0 \\{-}4\\ {-}1 \end{pmatrix}~+~s~\cdot~\begin{pmatrix} 4 \\ 0 \\ {-}1 \end{pmatrix}$
$(r \in \mathbb{R})$
4) Falsch - Die Richtungsvektoren sind kollinear / linear abhängig voneinander.
$\vec{x}~=~\begin{pmatrix} 5\\2\\{-}1 \end{pmatrix}~+~r~\cdot~\begin{pmatrix} {-}2\\4\\{-}3 \end{pmatrix}~+~s~\cdot~\begin{pmatrix} 6\\{-}12\\9 \end{pmatrix}$
$(r \in \mathbb{R})$
$\quad \Rightarrow \quad \begin{pmatrix} 6\\{-}12\\9 \end{pmatrix}~=~{-}3~\cdot~\begin{pmatrix} {-}2\\4\\{-}3 \end{pmatrix}$
5) Richtig - Die Gleichung ist eine Ebenengleichung. Hierfür werden die Richtungsvektoren überprüft.
$E:\vec{x}~=~\begin{pmatrix} 5\\2\\{-}1 \end{pmatrix}~+~r~\cdot~\begin{pmatrix} {-}2\\5\\1 \end{pmatrix}~+~s~\cdot~\begin{pmatrix} 4\\{-}2\\6 \end{pmatrix}$
$(r \in \mathbb{R})$
a) Richtungsvektoren sind ungleich dem Nullvektor:
$\vec{u}~=~\begin{pmatrix} {-}2\\5\\1 \end{pmatrix}~\neq~\begin{pmatrix} 0\\0\\ 0 \end{pmatrix} $
$\vec{v}~=~\begin{pmatrix} 4\\{-}2\\6 \end{pmatrix}~\neq~\begin{pmatrix} 0\\0\\ 0 \end{pmatrix} $
b) Richtungsvektoren sind nicht kollinear:
$\begin{pmatrix} {-}2\\5\\1 \end{pmatrix}~\neq~t~\cdot~\begin{pmatrix} 4\\{-}2\\6 \end{pmatrix}$
6) Falsch - Ein Richtungsvektor ist ein Nullvektor.
$\vec{x}~=~\begin{pmatrix} 5\\2\\{-}1 \end{pmatrix}~+~r~\cdot~\begin{pmatrix} {-}2\\5\\1 \end{pmatrix}~+~s~\cdot~\begin{pmatrix} 0\\0\\0 \end{pmatrix}$
$\vec{v}~=~\overrightarrow{AC}~=~\begin{pmatrix} 0\\0\\0 \end{pmatrix}$
-
Benenne die Elemente der Ebenengleichung im Koordinatensystem.
TippsDer Stützvektor $\color{#669900}{\vec{a}}$ führt zu einem Punkt auf der Ebene.
Punkte werden mit einem großen Buchstaben bezeichnet.
LösungIn dieser Aufgabe werden die Elemente der Parameterform einer Ebene dargestellt. Die allgemeine Ebenengleichung in Parameterform lautet:
$E:\vec{x}=\color{#669900} {\begin{pmatrix} a_1 \\a_2\\ a_3 \end{pmatrix}}\color{black}{~+~r~\cdot~}\color{#E96764}{\begin{pmatrix} u_1 \\ u_2 \\ u_3 \end{pmatrix}}\color{black}{~+~s~\cdot~}\color{#07B6E7}{\begin{pmatrix} v_1 \\ v_2 \\ v_3 \end{pmatrix}}\color{black}{\qquad(r, s \in \mathbb{R})}$
Der Stützvektor $\color{#669900}{\vec{a}}$ verläuft immer vom Ursprung zu einem beliebigen Punkt $\color{#669900}{A}$ auf der Ebene (dem Stützpunkt).
Die beiden Richtungsvektoren $\color{#E96764}{\vec{u}}$ und $\color{#07B6E7}{\vec{v}}$ spannen die Ebene auf. Sie können mit den Paramtern $r$ und $s$ so multipliziert werden, dass jeder Punkt auf der Ebene erreicht wird.
-
Analysiere die Ebenen.
TippsÜberlege, welche Punkte zur Ebene gehören. Achte darauf, ob Werte gleich bleiben.
Ebenen verlaufen parallel zu einer Koordinatenebene, wenn sie diese in keinem Punkt schneiden. Jeder Punkt $P_E$ auf der Ebene besitzt in diesem Fall eine gleichbleibende Koordinate.
Beispielsweise verläuft die nachfolgende Ebene auf der Höhe $y=5$ parallel zur $x$-$z$-Ebene.
$\vec{x}~=~\begin{pmatrix} 0\\5\\0 \end{pmatrix}~+~r~\cdot~\begin{pmatrix} 2\\0\\1 \end{pmatrix}~+~s~\cdot~\begin{pmatrix} 3\\0\\4 \end{pmatrix}~=~\begin{pmatrix} 2r+3s\\5\\1r+4s \end{pmatrix}$
Jeder Punkt $P_E(2r+3s\vert5\vert1r+4s)$ auf der Ebene besitzt denselben $y$-Wert $y=5$, während $x$ und $z$ verschiedene Werte annehmen können.
Ob ein Punkt in einer Ebene liegt, berechnest du, indem du die Punktkoordinaten als $\vec{x}$ einsetzt und das Gleichungssystem löst:
$E\!:\vec{x}~=~\begin{pmatrix} {-}1 \\0\\ 0 \end{pmatrix}~+~r~\cdot~\begin{pmatrix} 2 \\ 1 \\ 0 \end{pmatrix}~+~s~\cdot~\begin{pmatrix} {-}3 \\ 0 \\ 1 \end{pmatrix}$
Zu prüfender Punkt: $G({-}8\vert1\vert3)$.
$\begin{pmatrix} {-}8\\1\\3\end{pmatrix}=~\begin{pmatrix} {-}1 \\0\\ 0 \end{pmatrix}~+~r~\cdot~\begin{pmatrix} 2 \\ 1 \\ 0 \end{pmatrix}~+~s~\cdot~\begin{pmatrix} {-}3 \\ 0 \\ 1 \end{pmatrix}$
Nebenrechnung 1: Berechnen von $s$
$\begin{array}{rrrrrrrl} 3&=& 0 & + & 0r & + & 1s &\\ 3&=& 1s &~&~&~&~& \vert :1 \\ 3&=& s &~&~&~&~&~ \\ \end{array}$Nebenrechung 2: Berechnen von $r$
$\begin{array}{rrrrrrrl} 1&=& 0 & + & 1r & + & 0s &\\ 1&=& 1r &~&~&~&~ & \vert :1 \\ 1&=& r &~&~&~&~&~\\ \end{array}$Nebenrechung 3: Parameter prüfen
$\begin{array}{rrrrrrrl} {-}8&=&{-}1 & + & 2r & {-}& 3s &\vert ~r=1; s=3\\ {-}8&=&{-}1 & + & 2 & {-} & 9 &~\\ {-}8&=&{-}8 &~&~&~&~&~\\ \end{array}$$\begin{pmatrix} {-}8\\1\\3\end{pmatrix}=~\begin{pmatrix} {-}1 \\0\\ 0 \end{pmatrix}~+~1~\cdot~\begin{pmatrix} 2 \\ 1 \\ 0 \end{pmatrix}~+~3~\cdot~\begin{pmatrix} {-}3 \\ 0 \\ 1 \end{pmatrix}$
$\Rightarrow$ Der Punkt $G$ liegt in der Ebene $E$.
LösungIn dieser Aufgabe geht es darum, die Eigenschaften von Ebenen zu untersuchen.
Hierfür musst du herausfinden, welche Punkte $P(x_p\vert y_p\vert z_p)$ in der Ebene liegen.
Dies erkennst du, indem du gegebene Punktkoordinaten als $\vec{x}=\begin{pmatrix} x_p\\y_p\\z_p \end{pmatrix}$ einsetzt und das entstehende Gleichungssystem löst oder mithilfe der Parameterform
$\vec{x}~=\begin{pmatrix} x_p\\y_p\\z_p\end{pmatrix}=\begin{pmatrix} a_1\\a_2\\a_3 \end{pmatrix}~+~r~\cdot~\begin{pmatrix} u_1\\u_2\\u_3 \end{pmatrix}~+~s~\cdot~\begin{pmatrix} v_1\\v_2\\v_3 \end{pmatrix}$
schlussfolgerst, welche Punkte entstehen können.
Achte hierbei genau darauf, ob eine Koordinate in jedem Punkt der Ebene konstant ist.
Sie gibt an, wie sich die Ebene zu den Koordinatenebenen verhält. Es gilt:- $x = a$: Ebene verläuft parallel zur $y$-$z$-Ebene mit Abstand $a$.
- $y = a$: Ebene verläuft parallel zur $x$-$z$-Ebene mit Abstand $a$.
- $z = a$: Ebene verläuft parallel zur $x$-$y$-Ebene mit Abstand $a$.
Nachfolgend wird die richtige Zuordnung der Eigenschaften erklärt:
1) parelleler Verlauf zur $x$-$y$-Ebene
$\vec{x}~=~\begin{pmatrix} 0\\0\\1 \end{pmatrix}~+~r~\cdot~\begin{pmatrix} 3\\2\\0 \end{pmatrix}~+~s~\cdot~\begin{pmatrix} {-}5\\2\\0 \end{pmatrix}$ ... verläuft auf der Höhe $z=1$ parallel zur $x$-$y$-Ebene.
$\vec{x}~=~\begin{pmatrix} 0\\0\\1 \end{pmatrix}~+~r~\cdot~\begin{pmatrix} 3\\2\\0 \end{pmatrix}~+~s~\cdot~\begin{pmatrix} {-}5\\2\\0 \end{pmatrix}~=~\begin{pmatrix} 3r{-}5s\\2r+2s\\1 \end{pmatrix}$
Jeder Punkt $P_E(3r{-}5s\vert2r+2s\vert1)$ der Ebene liegt auf der Höhe $z=1$ und damit parallel zur $x$-$y$-Ebene.
2) Schnittpunkt mit der $x$-Achse
$\vec{x}~=~\begin{pmatrix} {-}2\\1\\3 \end{pmatrix}~+~r~\cdot~\begin{pmatrix} 2\\0\\{-}2 \end{pmatrix}~+~s~\cdot~\begin{pmatrix} {-}2\\{-}1\\3 \end{pmatrix}$ ... schneidet die $x$-Achse im Punkt $X(2\vert0\vert0)$.
$\begin{pmatrix} 2\\0\\0 \end{pmatrix}~=~\begin{pmatrix} {-}2\\1\\3 \end{pmatrix}~+~r~\cdot~\begin{pmatrix} 2\\0\\{-}2 \end{pmatrix}~+~s~\cdot~\begin{pmatrix} {-}2\\{-}1\\3 \end{pmatrix}$
Nebenrechung 1: Berechnen von $s$
$\begin{array}{rrrrrrrl} 0&=& 1 & + & 0r & {-} & 1s &\vert {-}1\\ {-}1&=& {-}1s &~&~&~&~& \vert :({-}1) \\ 1&=& s &~&~&~&~&~ \\ \end{array}$Nebenrechung 2: Berechnen von $r$
$\begin{array}{rrrrrrrl} 0&=&3 & {-} & 2r & + & 3s &\vert {-}3; s=1\\ {-}3&=& {-}2r &+&3&~&~ & \vert {-}3 \\ {-}6&=& {-}2r &~&~&~&~&\vert :({-}2) \\ 3&=& r &~&~&~&~&~\\ \end{array}$Nebenrechung 3: Parameter prüfen
$\begin{array}{rrrrrrrl} 2&=&{-}2 & + & 2r & {-} & 2s &\vert r=3; s=1\\ 2&=&{-}2 & + & 6 & {-} & 2 &~\\ 2&=&2 &~&~&~&~&~\\ \end{array}$$\quad \Rightarrow \quad \begin{pmatrix} 2\\0\\0 \end{pmatrix}~=~\begin{pmatrix} {-}2\\1\\3 \end{pmatrix}~+~3~\cdot~\begin{pmatrix} 2\\0\\{-}2 \end{pmatrix}~+~1~\cdot~\begin{pmatrix} {-}2\\{-}1\\3 \end{pmatrix}$
3) Punkt auf der Ebene
$\vec{x}~=~\begin{pmatrix} 5\\4\\{-}1 \end{pmatrix}~+~r~\cdot~\begin{pmatrix} {-}4\\0\\4 \end{pmatrix}~+~s~\cdot~\begin{pmatrix} 7\\{-}8\\0 \end{pmatrix}$ ... enthält den Punkt $D({-}1\vert{-}12\vert19)$.
$\begin{pmatrix} {-}1\\{-}12\\19\end{pmatrix}=~\begin{pmatrix} 5\\4\\{-}1 \end{pmatrix}~+~r~\cdot~\begin{pmatrix} {-}4\\0\\4 \end{pmatrix}~+~s~\cdot~\begin{pmatrix} 7\\{-}8\\0 \end{pmatrix}$
Nebenrechnung 1: Berechnen von $s$
$\begin{array}{rrrrrrrl} {-}12&=& 4 & + & 0r & {-} & 8s &\vert {-}4\\ {-}16&=& {-}8s &~&~&~&~& \vert :({-}8) \\ 2&=& s &~&~&~&~&~ \\ \end{array}$Nebenrechung 2: Berechnen von $r$
$\begin{array}{rrrrrrrl} 19&=&{-}1 & + & 4r & + & 0s &\vert +1\\ 20&=& 4r &~&~&~&~ & \vert :4 \\ 5&=& r &~&~&~&~&~\\ \end{array}$Nebenrechung 3: Parameter prüfen
$\begin{array}{rrrrrrrl} {-}1&=&5 & {-} & 4r & +& 7s &\vert r=5; s=2\\ {-}1&=&5 & {-} & 20 & +& 14 &~\\ {-}1&=&{-}1 &~&~&~&~&~\\ \end{array}$$\quad \Rightarrow \quad \begin{pmatrix} {-}1\\{-}12\\19\end{pmatrix}=~\begin{pmatrix} 5\\4\\{-}1 \end{pmatrix}~+~5~\cdot~\begin{pmatrix} {-}4\\0\\4 \end{pmatrix}~+~2~\cdot~\begin{pmatrix} 7\\{-}8\\0 \end{pmatrix}$
4) $x$-$z$-Ebene
$\vec{x}~=~\begin{pmatrix} 0\\0\\0 \end{pmatrix}~+~r~\cdot~\begin{pmatrix} 1\\0\\0 \end{pmatrix}~+~s~\cdot~\begin{pmatrix} 0\\0\\1 \end{pmatrix}$ ... definiert die $x$-$z$-Ebene.
$\vec{x}~=~\begin{pmatrix} 0\\0\\0 \end{pmatrix}~+~r~\cdot~\begin{pmatrix} 1\\0\\0 \end{pmatrix}~+~s~\cdot~\begin{pmatrix} 0\\0\\1 \end{pmatrix}~=~\begin{pmatrix} r\\0\\s \end{pmatrix}$
Jeder Punkt $P_E(r\vert0\vert s)$ auf der Ebene besitzt die $y$-Koordinate $y=0$, während $x$ und $z$ verschiedene Werte annehmen können. Die angegebene Ebene definiert somit die $x$-$z$-Ebene.
9.718
sofaheld-Level
6.600
vorgefertigte
Vokabeln
8.275
Lernvideos
38.567
Übungen
33.604
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Klassenstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung




 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?