Die I. und II. Hauptgruppe
Die Metalle der 1. und 2. Hauptgruppe zeichnen sich durch hohe Reaktivität aus und bilden mit Nichtmetallen Salze..
Inhaltsverzeichnis zum Thema
- I. Hauptgruppe – Alkalimetalle
- Alkalimetalle: Eigenschaften und Verwendung
- II. Hauptgruppe – Erdalkalimetalle
- Erdalkalimetalle: Eigenschaften und Verwendung
I. Hauptgruppe – Alkalimetalle
Die Elemente der ersten Hauptgruppe werden auch Alkalimetalle genannt. Eine Ausnahme bildet aber Wasserstoff. Bei Standardbedingungen liegt dieses gasförmig vor und weist keine metallischen Eigenschaften auf.
Zu den Alkalimetallen gehören Lithium, Natrium, Kalium, Rubidium, Cäsium und Francium. Alle Elemente der ersten Hauptgruppe weisen nur ein Außenelektron (Valenzelektron) auf. Um einen stabilen Zustand zu erreichen, ist eine Abgabe dieses Elektrons notwendig. So wird die nächstgelegene Edelgaskonfiguration erreicht und die Oktettregel erfüllt (außer bei Lithium). Die Alkalimetalle sind allesamt reaktionsfreudige Metalle, die in der Natur nur in Verbindungen vorliegen und nicht elementar in ihrer metallischen Form.
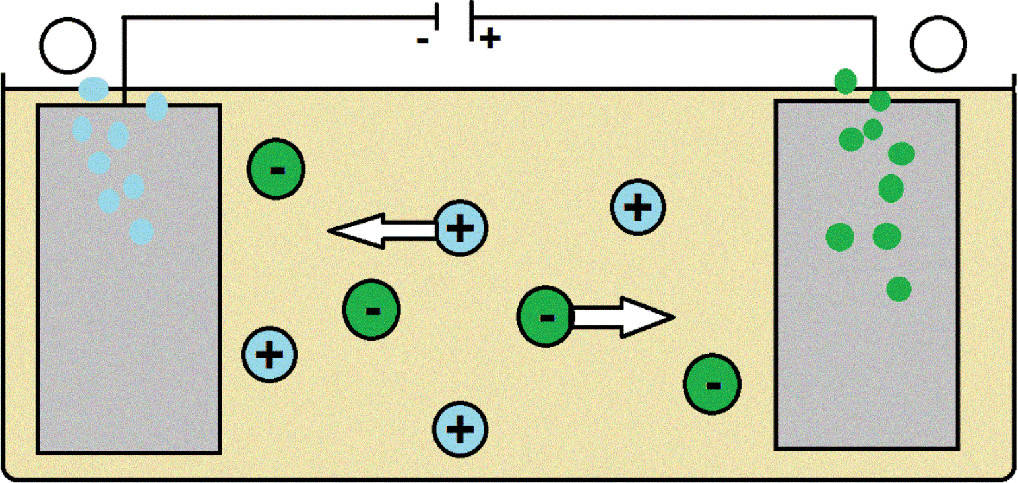
Die erste Herstellung eines Alkalimetalls gelang 1807 Humphry Davi. Er stellte aus dem Salz Kaliumhydroxid mittels Schmelzflusselektrolyse Kalium her. Auch heute noch werden die Alkalimetalle durch Schmelzflusselektrolyse gewonnen. Dabei wird das Salz aufgeschmolzen, wodurch Anionen und Kationen des Salzes frei beweglich werden. An der Kathode findet die Reduktion statt, wodurch die Kationen des Alkalimetalls zu ihrer elementare Form reduziert werden.
Alkalimetalle: Eigenschaften und Verwendung
Die Alkalimetalle sind in ihrer metallischen Form silbrig glänzend und weich. Diese Leichtmetalle kannst du mit einem Messer schneiden. Sie sind allerdings sehr reaktiv. Daher werden sie in Paraffinöl oder Petroleum gelagert. An der Luft reagieren sie sehr schnell mit Sauerstoff und bilden dann eine dunkle Oxidschicht. Alkalimetalle bilden einfach positiv geladene Ionen. Diese Kationen bilden mit Anionen Salze. Zwischen diesen entgegengesetzt geladenen Ionen herrschen starke elektrostatische Anziehungskräfte, wodurch sie einen hohen Schmelz- und Siedepunkt besitzen.
Einige Eigenschaften der Alkalimetalle zeigen Trends innerhalb der Gruppe der Alkalimetalle. Mit jeder neuen Periode (also innerhalb der Gruppe von oben nach unten) kommt eine neue Elektronenschale hinzu. Die Elektronen sind daher weiter vom Kern entfernt und die Anziehungskraft der Protonen auf die Außenelektronen wird immer schwächer. Daher nimmt innerhalb der Gruppe die Ionisierungsenergie von oben nach unten ab. Gleichzeitig nimmt die Reaktivität der Metalle von oben nach unten zu. Das ist z.B. an der Reaktion mit Wasser zu sehen. Ein Stück Natrium, in Wasser geworfen, zischt und flitzt auf der Oberfläche herum. Das gleiche Experiment mit Cäsium würde das Gefäß mit dem Wasser sprengen. Daher ist große Vorsicht beim Umgang mit diesen Metallen geboten.
Die Alkalimetalle zeigen charakteristische Flammenfarben. Diese dienen unter anderem als Vorprobe für den Nachweis dieser Elemente.

Aufgrund dieser leuchtenden Farben werden Alkalisalze oft in Feuerwerkskörpern eingesetzt. Andere Anwendungen sind die Seifenherstellung, die Verwendung als Trockenmittel (wegen der Reaktion mit Wasser) und organische Synthesen.
II. Hauptgruppe – Erdalkalimetalle
Zu den Erdalkalimetallen gehören die Elemente der zweiten Hauptgruppe. Dies sind Beryllium, Magnesium, Calcium, Strontium, Barium und das radioaktive Element Radium. Sie besitzen zwei Außenelektronen und sind ebenfalls reaktionsfreudige Metalle, die in der Natur nur in Verbindungen vorliegen. Um einen stabilen Zustand zu erreichen, müssen die Erdalkalimetalle zwei Elektronen abgeben. Sie bilden also zweifach positiv geladene Ionen. Wie die Alkalimetalle auch, werden sie mithilfe der Elektrolyse hergestellt. Außerdem können sie aber noch durch die Reduktion von Erdalkaliverbindungen (Salze oder Oxide) mit einem anderen Erdalkalimetall oder Kohlenstoff gewonnen werden.
Erdalkalimetalle: Eigenschaften und Verwendung
Die beiden ersten Gruppen ähneln sich stark in den Eigenschaften der Erdalkalimetalle. So zeigt sich auch in der zweiten Hauptgruppe ein Trend von Eigenschaften von oben nach unten. Die Ionisierungsenergie nimmt ab. Dabei steigt die Reaktivität und der Atomradius an. Die Härte nach Mohs nimmt ab und die Dichte nimmt zu. Die Erdalkalimetalle sind weniger reaktiv als die Alkalimetalle, da eine höhere Ionisierungsenergie aufgebracht werden muss, um beide Elektronen abzugeben. Sie reagieren gut mit Sauerstoff, Halogenen und Wasser. Dabei bilden Magnesium und Beryllium undurchlässige Oxidschichten. Diese werden als Passivierungsschichten bezeichnet. Auch diese Metalle zeigen farbige Flammen und werden für Feuerwerk eingesetzt.

Weitere Anwendungsgebiete sind die Herstellung von Legierungen für den Flugzeugbau und die Raumfahrt, die Verwendung als Reduktionmittel und der Einsatz für organische Synthesen. So werden Erdalkalimetalle z.B. in der Grignard-Reaktion zur Herstellung von sekundären und tertiären Alkoholen eingesetzt. Auch in der analytischen Chemie werden sie oft benötigt.
Alle Videos zum Thema
Videos zum Thema
Die I. und II. Hauptgruppe (3 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Die I. und II. Hauptgruppe (1 Arbeitsblatt)
Beliebteste Themen in Chemie
- Periodensystem
- Ammoniak Verwendung
- Entropie
- Salzsäure Steckbrief
- Kupfer
- Stickstoff
- Glucose Und Fructose
- Ethansäure
- Salpetersäure
- Redoxreaktion
- Schwefelsäure
- Natronlauge
- Graphit
- Legierungen
- Dipol
- Molare Masse, Stoffmenge
- Sauerstoff
- Elektrolyse
- Bor
- Alkane
- Verbrennung Alkane
- Chlor
- Elektronegativität
- Tenside
- Toluol, Toluol Herstellung
- Wasserstoffbrückenbindung
- fraktionierte Destillation
- Carbonsäure
- Ester
- Harnstoff, Kohlensäure
- Reaktionsgleichung Aufstellen
- Redoxreaktion Übungen
- Stärke und Cellulose Chemie
- Süßwasser und Salzwasser
- Katalysator
- Ether
- Primärer Alkohol, Sekundärer Alkohol, Tertiärer Alkohol
- Van-der-Waals-Kräfte
- Oktettregel
- Kohlenstoffdioxid, Kohlenstoffmonoxid, Oxide
- Alfred Nobel
- Wassermolekül
- Ionenbindung
- Phosphor
- Saccharose Und Maltose
- Aldehyde
- Kohlenwasserstoff
- Kovalente Bindung
- Wasserhärte
- Peptidbindung






 I. Hauptgruppe – Überblick
I. Hauptgruppe – Überblick









