Reaktionsordnungen
Reaktionen unterscheiden sich in ihrer Reaktionsgeschwindigkeit. Wir unterscheiden in 0. Ordnung, 1. Ordnung, 2. Ordnung oder höhere Ordnung.
Beliebteste Videos
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
Kinetik und Reaktionsgeschwindigkeit
Die Kinetik ist ein Teilbereich der physikalischen Chemie. Sie beschäftigt sich mit den zeitlichen Abläufen von chemischen Reaktionen. Besonders wichtig für die Kinetik ist dabei die Größe der Reaktionsgeschwindigkeit.
Sie ist definiert als die Veränderung der Konzentration pro verstrichenes Zeitintervall. Die Reaktionsgeschwindigkeit wird wie folgt mathematisch ausgedrückt:
$v=~\frac{\Delta c}{\Delta t}$.
Bei einer einfachen Reaktion wie $A \longrightarrow~B$ ist die Geschwindigkeit der Hinreaktion
$v=~-\frac{\Delta c(A)}{\Delta t}$.
Da die Reaktionsgeschwindigkeit positiv sein muss und die Konzentration von A fällt, steht am Anfang der Gleichung ein negatives Vorzeichen. Für die Rückreaktion fehlt dieses Vorzeichen. Für eine chemische Reaktion kann man immer eine Reaktionsgleichung aufstellen. Ist diese komplex, kann sie meist in Elementarreaktionen zerlegt werden. Das sind Reaktionen, die sich nicht weiter aufgliedern lassen. Durch diese Elementarreaktionen kann man auf den Mechanismus der Reaktion schließen. Außerdem ist es möglich, mithilfe dieser Reaktionen die Reaktionsordnung der einzelnen Reaktanten zu bestimmen. Die Reaktionsordnung ergibt sich aus dem Exponenten, mit dem der Reaktant in das Geschwindigkeitsgesetz eingeht. Die Summe aller Exponenten der Reaktanten ergibt dann die Gesamtordnung der Reaktion.
Nullte Ordnung
Eine Reaktion nullter Ordnung ist unabhängig von der Konzentration des Reaktionsteilnehmers. Dadurch ist die Reaktionsgeschwindigkeit konstant:
$v=~-\frac{\Delta c(A)}{\Delta t}= k$.
Das wird ausgedrückt durch die Geschwindigkeitskonstante $k$. Der Reaktant A geht hier also mit dem Exponenten 0 ins Geschwindigkeitsgesetz ein. Beispiele für Reaktionen nullter Ordnung sind photochemische und katalytische Prozesse. Diese hängen dann nur von der Lichtintensität bzw. von der Oberfläche des Katalysators ab und sind von der Konzentration unabhängig.

Erste Ordnung
Eine Reaktion erster Ordnung ist z.B. eine radioaktive Zerfallsreaktion und auch einige katalytische Prozesse fallen darunter. Beispielhaft soll die Reaktion $A \longrightarrow~B + C$ für eine solche Reaktion stehen.
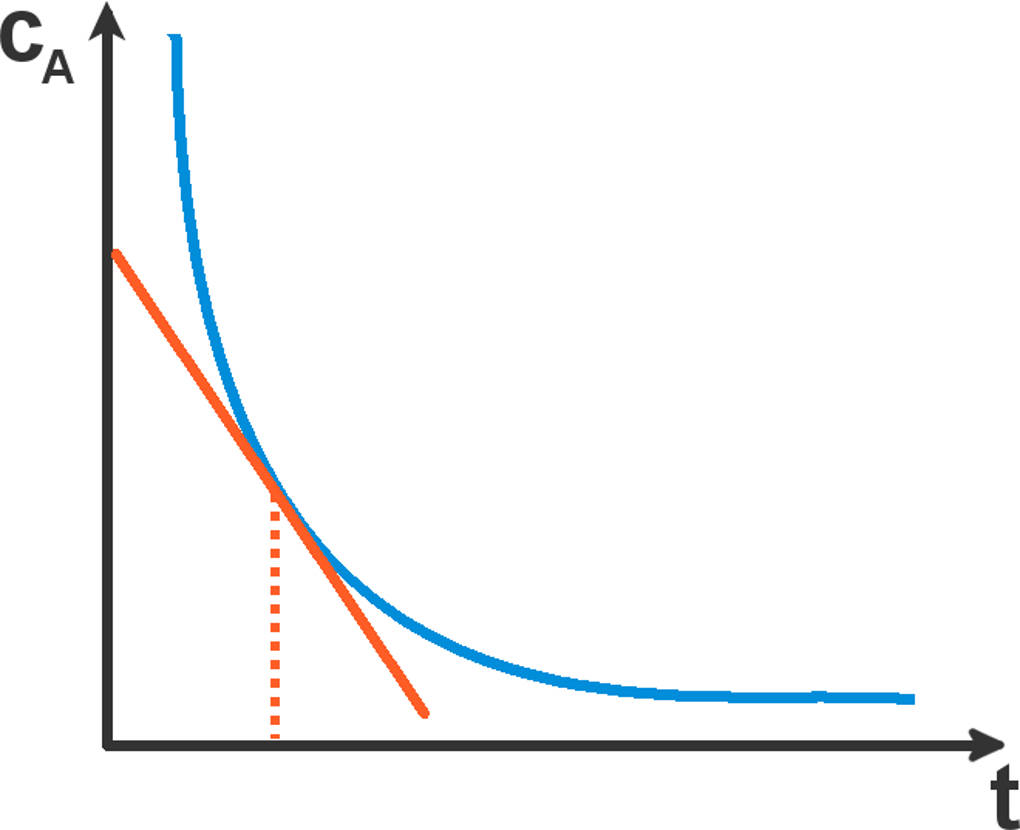
Das Geschwindigkeitsgesetz sagt uns, dass die Reaktionsgeschwindigkeit die negative partielle Ableitung der Konzentration von A durch die Zeit ist:
$v=~-\frac{d [A]}{d t}$.
Abgeleitet ergibt sich daraus $v= k \cdot [A]$. A geht also mit dem Exponenten 1 in die Gleichung ein. Das Ganze muss nun noch in den Grenzen 0 bis t integriert werden. Das geschieht mit der Gleichung für die Konzentration $[A]= [A]_0 \cdot e^{-k \cdot t}$. Für $v$ ergibt sich dann folgende Gleichung:
$v = -k \cdot [A]_0 \cdot e^{-k \cdot t}$.
Zweite Ordnung
Reaktionen zweiter Ordnung kommen recht häufig vor. Es reagieren zwei Edukte zu einem oder mehreren Produkten $A + B \longrightarrow C$. Die Geschwindigkeit der Reaktion ist also davon abhängig, wie oft sich die beiden Stoffe treffen, also von deren Konzentration. Das Geschwindigkeitsgesetz sieht für diese Reaktion wie folgt aus:
$v=~-\frac{d [A]}{d t}= -\frac{d [B]}{d t}= k\cdot [A]\cdot [B]$.
Wenn A und B dieselben Konzentrationen aufweisen, kann man vereinfachen, indem man A mit B gleichsetzt. Dadurch erhält man $v= k\cdot [A]^2$. Integriert von 0 bis t ergibt sich dann für $[A]_t$:
$[A]_t= \frac{1}{2k \cdot t + \frac{1}{[A]_0}}$.
Es gibt auch noch Reaktionen dritter Ordnung. Diese sind allerdings selten, da ein Zusammentreffen von drei und mehr Teilchen zur selben Zeit sehr unwahrscheinlich ist.
Setzt sich die Gesamtreaktion aus Teilreaktionen unterschiedlicher Ordnung zusammen, können sich auch Mischordnungen wie $0,5$, $1,5$, $2,5$ usw. ergeben. Jedoch bestimmt immer der langsamste Schritt die Reaktionsgeschwindigkeit.
Alle Videos zum Thema
Videos zum Thema
Reaktionsordnungen (1 Video)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Reaktionsordnungen (1 Arbeitsblatt)
Beliebteste Themen in Chemie
- Periodensystem
- Ammoniak Verwendung
- Entropie
- Salzsäure Steckbrief
- Kupfer
- Stickstoff
- Glucose Und Fructose
- Salpetersäure
- Redoxreaktion
- Schwefelsäure
- Natronlauge
- Graphit
- Legierungen
- Dipol
- Molare Masse, Stoffmenge
- Sauerstoff
- Elektrolyse
- Bor
- Alkane
- Chlor
- Elektronegativität
- Tenside
- Toluol, Toluol Herstellung
- Wasserstoffbrückenbindung
- Fraktionierte Destillation Von Erdöl
- Carbonsäure
- Ester
- Harnstoff, Kohlensäure
- Reaktionsgleichung Aufstellen
- Cellulose Und Stärke Chemie
- Süßwasser Und Salzwasser
- Katalysator
- Ether
- Primärer Alkohol, Sekundärer Alkohol, Tertiärer Alkohol
- Van-der-Waals-Kräfte
- Oktettregel
- Kohlenstoffdioxid, Kohlenstoffmonoxid, Oxide
- Alfred Nobel Und Die Dynamit Entdeckung
- Wassermolekül
- Ionenbindung
- Phosphor
- Saccharose Und Maltose
- Kohlenwasserstoff
- Kovalente Bindungen
- Wasserhärte
- Peptidbindung
- Fermentation
- Nernst-Gleichung, Konzentrationsabhängigkeit Des Elektrodenpotentials
- Ethanol Als Lösungsmittel
- Kohlenstoff




 Reaktion dritter Ordnung
Reaktion dritter Ordnung









