Ganzrationale und gebrochenrationale Funktionen – Verhalten im Unendlichen
Lerne, wie du dich auf Englisch effektiv entschuldigst und dein Verhalten rechtfertigst. Von flüchtigen Entschuldigungen bis hin zu formellen, wir haben alle nützlichen Vokabeln und Beispielsätze für dich. Wie entschuldigt man sich für Lärm? Wie drückt man Höflichkeit aus? Entdecke das und vieles mehr! Neugierig geworden? Dann lerne jetzt, wie du dich wie ein Profi entschuldigst!
- Verhalten im Unendlichen – Benötigtes Vorwissen
- Verhalten im Unendlichen von ganzrationalen Funktionen
- Höchste Potenz mit ungeradem Exponenten im Unendlichen
- Höchste Potenz mit geradem Exponenten im Unendlichen
- Verhalten im Unendlichen von gebrochenrationalen Funktionen
- Die höchste $x$-Potenz ist im Nenner
- Die höchste $x$-Potenz ist im Zähler
- Gleich hohe höchste $x$-Potenzen
- Verhalten im Unendlichen – Zusammenfassung
- Häufig gestellte Fragen zum Thema Verhalten im Unendlichen
in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
Lerntext zum Thema Ganzrationale und gebrochenrationale Funktionen – Verhalten im Unendlichen
Verhalten im Unendlichen – Benötigtes Vorwissen
Für dieses Thema ist es notwendig zu wissen, was ganzrationale und gebrochenrationale Funktionen sind.
Allgemeine Form einer ganzrationalen Funktion:
$f(x) = a_{n} \cdot x^{n} + a_{n-1} \cdot x^{n-1} + … + a_{1} \cdot x + c$
Allgemeine Form einer gebrochenrationalen Funktion:
$f(x) = \dfrac{a_{n} \cdot x^{n} + a_{n-1} \cdot x^{n-1} + … + a_{1} \cdot x + c}{b_{m} \cdot x^{m} + b_{m-1} \cdot x^{m-1} + … + b_{1} \cdot x + d}$
Außerdem ist der Prozess des Ausklammerns sehr wichtig. Weiterhin sollten der Grenzwert und die Grenzwertsätze bekannt und verstanden worden sein.
Der Grenzwert einer Funktion beschreibt das Verhalten dieser Funktion unter bestimmten Bedingungen. Mit Grenzwerten kann das Verhalten von Funktionen im positiven und negativen Unendlichen untersucht werden.
Der Grenzwert wird in mathematischer Schreibweise mit $\lim\limits_{x \to a}$ bezeichnet.
Die vier Grenzwertsätze:
$\lim\limits_{x \to a} (f(x) + g(x)) = \lim\limits_{x \to a} f(x) + \lim\limits_{x \to a} g(x)$
$\lim\limits_{x \to a} (f(x) – g(x)) = \lim\limits_{x \to a} f(x) – \lim\limits_{x \to a} g(x)$
$\lim\limits_{x \to a} (f(x) \cdot g(x)) = \lim\limits_{x \to a} f(x) \cdot \lim\limits_{x \to a} g(x)$
$\lim\limits_{x \to a} \dfrac{f(x)}{g(x)} = \dfrac{\lim\limits_{x \to a} f(x)}{\lim\limits_{x \to a} g(x)}$
Wie wir dieses Wissen anwenden können, um das Verhalten von Funktionen im Unendlichen zu bestimmen, schauen wir uns jetzt anhand konkreter Beispiele an.
Verhalten im Unendlichen von ganzrationalen Funktionen
Gegeben ist folgende ganzrationale Funktion:
$f(x) = 3x^5 – 2x^4 + 7x^2 – 32$
Von dieser Funktion soll nun das Verhalten im positiven sowie negativen Unendlichen bestimmt werden. Bei ganzrationalen Funktionen handelt es sich stets um Summenterme. Daher kann die Funktion in einzelne Summanden unterteilt werden, um sie zu untersuchen. Nach dem ersten Grenzwertsatz gilt damit:
$\lim\limits_{x \to \infty} (3x^5 – 2x^4 + 7x^2 – 32) = \lim\limits_{x \to \infty} 3x^5 + \lim\limits_{x \to \infty} –2x^4 + \lim\limits_{x \to \infty} 7x^2 + \lim\limits_{x \to \infty} –32$
Die einzelnen Summanden können mit dem Grenzwert besser untersucht werden. Es gilt:
$\underbrace{\lim\limits_{x \to \infty} 3x^5}_{\rightarrow +\infty} + \underbrace{\lim\limits_{x \to \infty} –2x^4}_{\rightarrow –\infty} + \underbrace{\lim\limits_{x \to \infty} 7x^2}_{\rightarrow +\infty} + \underbrace{\lim\limits_{x \to \infty} –32}_{\rightarrow –32}$
Dadurch, dass die Summanden hier für $x \rightarrow \infty$ aber sowohl gegen $+\infty$ als auch gegen $–\infty$ streben, lässt sich noch keine genaue Aussage für den Grenzwert der gesamten Funktion treffen. Um dies genauer zu untersuchen, klammern wir die höchste $x$-Potenz aus:
$f(x) = 3x^5 – 2x^4 + 7x^2 – 32 = x^5 \cdot (3 – 2 \cdot \frac{1}{x} + 7 \cdot \frac{1}{x^3} – 32 \cdot \frac{1}{x^5})$
Bei der Betrachtung dieses Grenzwertes mithilfe des ersten und dritten Grenzwertsatzes kann folgende Aussage getroffen werden:
$\lim\limits_{x \to \infty} (x^5 \cdot (3 – 2 \cdot \frac{1}{x} + 7 \cdot \frac{1}{x^3} – 32 \cdot \frac{1}{x^5})) = \lim\limits_{x \to \infty} x^5 \cdot \lim\limits_{x \to \infty} (3 – 2 \cdot \frac{1}{x} + 7 \cdot \frac{1}{x^3} – 32 \cdot \frac{1}{x^5}) = \underbrace{\lim\limits_{x \to \infty} x^5}_{\rightarrow +\infty} \cdot (\underbrace{\lim\limits_{x \to \infty} 3}_{\rightarrow 3} + \underbrace{\lim\limits_{x \to \infty}–2 \cdot \frac{1}{x}}_{\rightarrow 0} + \underbrace{\lim\limits_{x \to \infty} 7 \cdot \frac{1}{x^3}}_{\rightarrow 0} + \underbrace{\lim\limits_{x \to \infty} –32 \cdot \frac{1}{x^5}}_{\rightarrow 0})\longrightarrow +\infty$
Also strebt der Grenzwert der Funktion für $x \rightarrow \infty$ gegen $+\infty$. So kann auch für $x \rightarrow –\infty$ vorgegangen werden, doch aufgrund der Komplexität der Vorgehensweise schauen wir uns die Regeln an, die wir aus dem obigen Beispiel ableiten können. Dazu können wir einen Merksatz formulieren.
Um den Grenzwert einer ganzrationalen Funktion für $x \rightarrow \pm \infty$ zu bestimmen, muss die höchste Potenz der Funktion betrachtet werden. Bei dieser sind zwei Eigenschaften von Relevanz:
Ist der entsprechende Exponent gerade oder ungerade? Ist der Vorfaktor der Potenz negativ oder positiv?
Diese Vorgehensweise nutzen wir nun für die Betrachtung der obigen Funktion für $x \rightarrow –\infty$. Die höchste Potenz lautet $3x^{5}$, damit ist der Exponent ungerade und die Potenz hat einen positiven Vorfaktor ($+3$). Für $x \rightarrow –\infty$ strebt die Potenz also gegen $–\infty$. Damit strebt auch die ganze Funktion für $x \rightarrow –\infty$ gegen $–\infty$. Um die Notwendigkeit der Untersuchung der beiden Eigenschaften der höchsten Potenz zu verdeutlichen, werden im Folgenden einige Potenzen und ihre Grenzwerte dargestellt.
Höchste Potenz mit ungeradem Exponenten im Unendlichen
$\lim\limits_{x \to \infty} 3x^5 \longrightarrow \infty$
$\lim\limits_{x \to \infty} –3x^5 \longrightarrow –\infty$
$\lim\limits_{x \to –\infty} 3x^5 \longrightarrow –\infty$
$\lim\limits_{x \to –\infty} –3x^5 \longrightarrow \infty$
| Funktionsgraphen ($3x^{5}$ in grün, $-3x^{5}$ in orange) |
|---|
 |
Höchste Potenz mit geradem Exponenten im Unendlichen
$\lim\limits_{x \to \infty} 3x^4 \longrightarrow \infty$
$\lim\limits_{x \to \infty} –3x^4 \longrightarrow –\infty$
$\lim\limits_{x \to –\infty} 3x^4 \longrightarrow \infty$
$\lim\limits_{x \to –\infty} –3x^4 \longrightarrow –\infty$
| Funktionsgraphen ($3x^{4}$ in orange, $-3x^{4}$ in lila) |
|---|
 |
Verhalten im Unendlichen von gebrochenrationalen Funktionen
Bei dem Verhalten im Unendlichen von gebrochenrationalen Funktionen können wir zwischen drei Arten von Brüchen unterscheiden. Diese werden im Folgenden vorgestellt.
Die höchste $x$-Potenz ist im Nenner
Gegeben ist folgende ganzrationale Funktion:
$g(x) = \dfrac{2x^4 – 5x^2 – 7x}{6x^7 + 3x^3 – 15}$
Nach dem vierten Grenzwertsatz könnten hier Zähler und Nenner getrennt untersucht werden. Doch auch hier stellt sich die Frage, was nun das Verhalten der gesamten Funktion im Unendlichen beschreibt. Wir klammern erneut aus, allerdings werden zunächst die beiden höchsten Potenzen von Zähler und Nenner verglichen. Die niedrigere dieser beiden höchsten Potenzen wird sowohl im Zähler als auch im Nenner ausgeklammert. In der Funktion $g(x)$ ist die höchste Potenz des Zählers $2x^{4}$ und die des Nenners $6x^{7}$, also wird die Potenz $x^{4}$ bei beiden ausgeklammert.
$\dfrac{2x^4 – 5x^2 – 7x}{6x^7 + 3x^3 – 15} = \dfrac{x^4 \cdot (2 – \frac{5}{x^2} – \frac{7}{x^3})}{x^4 \cdot (6x^3 + \frac{3}{x} – \frac{15}{x^4})} = \dfrac{2 – \frac{5}{x^2} – \frac{7}{x^3}}{6x^3 + \frac{3}{x} – \frac{15}{x^4}}$
Die ausgeklammerte Potenz konnte aus dem Bruch gekürzt werden. Nun kann der Grenzwert besser untersucht werden, und zwar wie folgt:
$\lim\limits_{x \to \infty} \dfrac{\overbrace{2}^{\rightarrow 2} \overbrace{– \frac{5}{x^2}}^{\rightarrow 0} \overbrace{– \frac{7}{x^3}}^{\rightarrow 0}}{\underbrace{6x^3}_{\rightarrow \infty} + \underbrace{\frac{3}{x}}_{\rightarrow 0} \underbrace{– \frac{15}{x^4}}_{\rightarrow 0}} \longrightarrow \dfrac{2}{\underbrace{6x^3}_{\rightarrow \infty}} \longrightarrow 0$
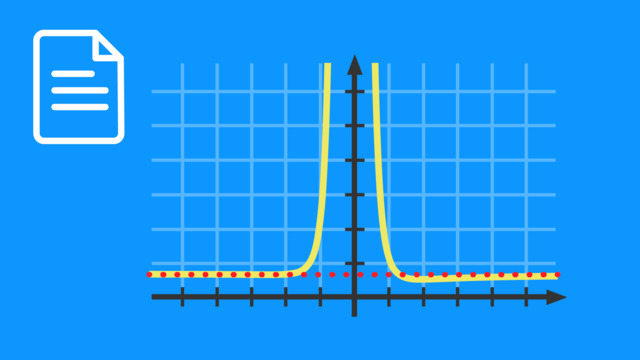
Damit verläuft die Funktion für $x \rightarrow \infty$ gegen $0$. Da die $0$ kein Vorzeichen hat, kann sich dieses für $x \rightarrow –\infty$ nicht ändern. Also verläuft die Funktion auch für $x \rightarrow –\infty$ gegen $0$.
| Funktionsgraph von $g(x)$ |
|---|
 |
Wir rekonstruieren aus dem Beispiel wieder einen Merksatz.
Ist beim Vergleich der höchsten Potenzen im Zähler und Nenner einer gebrochenrationalen Funktion die im Nenner höher, strebt die Funktion für ${x \rightarrow \pm \infty}$ gegen $0$.
Die höchste $x$-Potenz ist im Zähler
Schauen wir uns nun den entgegengesetzten Fall an. Wir betrachten folgende Funktion:
$h(x) = \dfrac{–3x^7 + 5x^3}{6x^5 – x^2 + 3x}$
Auch hier klammern wir die niedrigere höchste Potenz von Zähler und Nenner aus. Das ist in diesem Fall $x^{5}$.
$\dfrac{x^5 \cdot (–3x^2 + \frac{5}{x^2})}{x^5 \cdot (6 – \frac{1}{x^3} + \frac{3}{x^4})} = \lim\limits_{x \to \infty} \dfrac{\overbrace{–3x^2}^{\rightarrow –\infty} + \overbrace{\frac{5}{x^2}}^{\rightarrow 0}}{\underbrace{6}_{\rightarrow 6} – \underbrace{\frac{1}{x^3}}_{\rightarrow 0} + \underbrace{\frac{3}{x^4}}_{\rightarrow 0}}$
Wie man sieht, müssen die Regeln für ganzrationale Funktionen angewandt werden, wenn die höchste Potenz im Zähler ist. Damit sind wieder die Art des Exponenten (gerade/ungerade) und das Vorzeichen der Potenzen von Relevanz. Da hier nach der Grenzwertbetrachtung lediglich der Term $\frac{–3x^{2}}{6}$ übrig bleibt, kann ermittelt werden, dass die Funktion für $x \rightarrow \infty$ gegen $–\infty$ geht. Für $x \rightarrow –\infty$ geht die Funktion wegen des geraden Exponenten und des Vorzeichens auch gegen $–\infty$.
| Funktionsgraph von $h(x)$ |
|---|
 |
Wir rekonstruieren aus dem Beispiel wieder einen Merksatz.
Ist beim Vergleich der höchsten Potenzen im Zähler und Nenner einer gebrochenrationalen Funktion die im Zähler höher, müssen die Regeln für ganzrationale Funktionen angewandt werden und die Funktion strebt für ${x \rightarrow \pm \infty}$ gegen ${\pm \infty}$.
Gleich hohe höchste $x$-Potenzen
Schauen wir uns nun den letzten Fall an. Wir betrachten folgende Funktion:
$i(x) = \dfrac{2x^4 – 3x^2 + 6}{5x^4 + 2x^3}$
Auch hier klammern wir die niedrigere höchste Potenz von Zähler und Nenner aus. Das ist in diesem Fall $x^{4}$.
$\dfrac{x^4 \cdot (2 – \frac{3}{x^2} + \frac{6}{x^4})}{x^4 \cdot (5 + \frac{2}{x})} = \lim\limits_{x \to \infty} \dfrac{\overbrace{2}^{\rightarrow 2} – \overbrace{\frac{3}{x^2}}^{\rightarrow 0}}{\underbrace{5}_{\rightarrow 5} + \underbrace{\frac{2}{x}}_{\rightarrow 0}} \longrightarrow \frac{2}{5}$
Wie man sieht, fallen die Terme durch das Ausklammern und den Grenzwert so weit weg, dass nach dem Grenzwert nur noch die Koeffizienten vor den höchsten Potenzen übrig bleiben.
| Funktionsgraph von $i(x)$ |
|---|
 |
Wir rekonstruieren aus dem Beispiel wieder einen Merksatz.
Sind beim Vergleich der höchsten Potenzen in Zähler und Nenner einer gebrochenrationalen Funktionen beide gleich hoch, strebt die Funktion gegen einen bestimmten Wert, nämlich gegen den Bruch, der aus den beiden Koeffizienten der höchsten Potenz besteht.
Verhalten im Unendlichen – Zusammenfassung
Bei der Betrachtung von ganzrationalen Funktionen im Unendlichen muss die höchste Potenz der Funktion betrachtet werden. Dann gilt:
- Positives Vorzeichen und gerader Exponent: Für $x \rightarrow \pm \infty$ geht die Funktion gegen $\infty$.
- Positives Vorzeichen und ungerader Exponent: Für $x \rightarrow \infty$ geht die Funktion gegen $\infty$ und für $x \rightarrow –\infty$ geht die Funktion gegen $–\infty$.
- Negatives Vorzeichen und gerader Exponent: Für $x \rightarrow \pm \infty$ geht die Funktion gegen $–\infty$.
- Negatives Vorzeichen und ungerader Exponent: Für $x \rightarrow \infty$ geht die Funktion gegen $–\infty$ und für $x \rightarrow –\infty$ geht die Funktion gegen $\infty$.
Bei der Betrachtung von gebrochenrationalen Funktionen im Unendlichen muss darauf geachtet werden, wo oder ob im Bruch eine höchste Potenz zu finden ist.
- Ist die höchste Potenz im Nenner, verläuft die Funktion für $x \rightarrow \pm \infty$ gegen $0.$
- Ist die höchste Potenz im Zähler, müssen die obigen Regeln für ganzrationale Funktionen angewandt werden. Dementsprechend verläuft die Funktion für $x \rightarrow \pm \infty$ gegen $\pm \infty$.
- Ist die höchste Potenz sowohl im Zähler als auch im Nenner, verläuft die Funktion für $x \rightarrow \pm \infty$ gegen den Bruch der Koeffizienten vor den größten Potenzen.
Häufig gestellte Fragen zum Thema Verhalten im Unendlichen
Ganzrationale und gebrochenrationale Funktionen – Verhalten im Unendlichen Übung
-
Gib an, wie der Grenzwert von ganzrationalen Funktionen bestimmt werden kann.
TippsBeachte, dass $\lim\limits_{x\to\infty} x^n=\infty$ für alle $n\in\mathbb{N}$ gilt.
Es gilt $\lim\limits_{x\to\infty} \frac{Z}{x^n}=0$ mit $n\in\mathbb{N}$ und $Z\in\mathbb{R}$.
Wenn ein Faktor gegen eine feste Zahl und der andere gegen $\infty$ strebt, dann strebt das Produkt gegen $\infty$.
LösungGegeben ist die ganzrationale Funktion $f$ mit $f(x)=x^4-5x^3+7x^2-8x+9$. Wenn du die einzelnen Grenzwerte $\lim\limits_{x\to\infty}$ der Potenzen betrachtest, stellst du fest, dass sowohl $+\infty$ als auch $-\infty$ dabei herauskommt. Du kannst so also nicht entscheiden, wogegen die ganzrationale Funktion strebt.
Ein möglicher Trick ist es nun, die Potenz mit dem höchsten Exponenten auszuklammern. Du erhältst:
$f(x)=x^4\cdot\left(1-\frac5x+\frac7{x^2}-\frac8{x^3}+\frac9{x^4}\right)$
Schau dir nun zunächst den Grenzwert für den Term in der Klammer an:
$\lim\limits_{x\to \infty}\left(1-\frac5x+\frac7{x^2}-\frac8{x^3}+\frac9{x^4}\right)=1-0+0-0+0=1$
Warum ist das so? Wenn du eine feste Zahl durch eine Potenz in $x$ dividierest, geht der resultierende Term gegen $0$, wenn $x$ gegen $\infty$ geht.
Da $\lim\limits_{x\to\infty} x^4 = \infty$ gilt, erhältst du auch insgesamt:
$\lim\limits_{x\to \infty}f(x)=\infty$
Aus diesem Ergebnis kannst du die Erkenntnis ziehen, dass bei ganzrationalen Funktionen der Summand mit dem größten Exponenten ausschlaggebend ist, wenn es um das Verhalten im Unendlichen geht.
-
Fasse die Grenzwerte bei ganzrationalen Funktionen in einer Tabelle zusammen.
TippsSchau dir das Beispiel $f(x)=x^2$ an. Der zugehörige Funktionsgraph ist eine Parabel.
- Wenn du eine negative Zahl mit einem geraden Exponenten potenzierst, ist das Ergebnis positiv.
- Wenn du eine negative Zahl mit einem ungeraden Exponenten potenzierst, ist das Ergebnis negativ.
Hier siehst du zum Beispiel den Funktionsgraphen der Funktion $f$ mit $f(x)=x^3$. Der größte (und einzige) Exponent ist ungerade.
Beim geraden höchsten Exponenten stimmen die Grenzwerte für $x\to\infty$ und $x\to-\infty$ überein. Beim ungeraden höchsten Exponenten ändert sich das Verhalten.
LösungHier siehst du die komplette Tabelle. Schreibe dir diese auf, dann kannst du die Grenzwerte immer direkt angeben.
Ganzrationale Funktionen streben für $x\to\infty$ beziehungsweise $x\to-\infty$ immer gegen $+\infty$ oder $-\infty$.
Du musst also jeweils entscheiden, welches Vorzeichen der Grenzwert hat. Dies hängt vom höchsten Exponenten sowie dem höchsten Koeffizienten ab.
Die allgemeine Form einer ganzrationalen Funktion siehst du hier:
$f(x)=a_nx^n+a_{n-1}x^{n-1}+...+a_2x^2+a_1x+a_0$
Der höchste Exponent ist $n$ und der Koeffizient der größten Potenz ist $a_n$. Es muss $a_n\neq 0$ gelten.
Du kannst nun die folgenden zwei Fälle (mit je zwei Fällen) unterscheiden:
Exponent in der höchsten Potenz gerade
Da eine negative Zahl mit einem geraden Exponenten potenziert eine positive Zahl ergibt, folgt:
- $a_n>0$: $\lim\limits_{x\to\infty}f(x)=\lim\limits_{x\to-\infty}f(x)=\infty$
- $a_n<0$: $\lim\limits_{x\to\infty}f(x)=\lim\limits_{x\to-\infty}f(x)=-\infty$
Da eine negative Zahl mit einem geraden Exponenten potenziert eine negative Zahl ergibt, folgt:
- $a_n>0$: $\lim\limits_{x\to\infty}f(x)=\infty$ und $\lim\limits_{x\to-\infty}f(x)=-\infty$
- $a_n<0$: $\lim\limits_{x\to\infty}f(x)=-\infty$ sowie $\lim\limits_{x\to-\infty}f(x)=\infty$
-
Beschreibe, wie der Grenzwert einer gebrochenrationalen Funktion bestimmt wird.
TippsBeachte, dass $\dfrac1{x^n}$ für $x\to\pm\infty$ gegen $0$ geht. Dabei ist der Exponent $n\in\mathbb{N}$.
Schau dir ein Beispiel für übereinstimmende höchste Potenzen an:
$\lim\limits_{x\to\infty} f(x)=\lim\limits_{x\to\infty} \dfrac{2x^2}{3x^2}=\frac{2}{3}$
Zum Beispiel geht $f(x)=\dfrac{x^3+1}{-x+2}$ für $x\to \infty$ gegen $-\infty$.
LösungBetrachte die gebrochenrationale Funktion $f$ mit folgender Funktionsgleichung:
$f(x)=\frac{x^3-2x^2+1000}{x^5-6x+1}$
Du siehst, dass für $x\to\infty$ sowohl der Term im Zähler als auch der im Nenner gegen $\infty$ geht. Du kannst also die Grenzwertsätze zur Berechnung des Grenzwertes von Quotienten nicht anwenden.
Wenn du nun sowohl im Zählerterm als auch im Nennerterm $x^3$, also die kleinere der beiden jeweiligen größten Potenzen, ausklammerst, erhältst du:
$f(x)=\dfrac{x^3\cdot\left(1-\frac2x+\frac{1000}{x^3}\right)}{x^3\cdot\left(x^2-\frac6{x^2}+\frac1{x^3}\right)}$
Du kannst die Potenz $x^3$ nun kürzen und kommst so zu:
$f(x)=\dfrac{1-\frac2x+\frac{1000}{x^3}}{x^2-\frac6{x^2}+\frac1{x^3} }$
Für $x\to\infty$ geht der Term im Zähler gegen $1$ und der im Nenner gegen $\infty$. Insgesamt gilt also:
$\lim\limits_{x\to\infty}=0$
In diesem Beispiel ist die höchste Potenz im Zählerterm $(x^3)$ kleiner als die im Nennerterm $(x^5)$.
Du kannst ganz allgemein drei Fälle unterscheiden. Hierfür schauen wir uns eine allgemeine gebrochenrationale Funktion $f$ an:
$f(x)=\dfrac{a_nx^n+...+a_1x+a_0}{b_mx^m+...+b_1x+b_0}$
Dabei muss sowohl $a_n\neq 0$ als auch $b_m\neq0$ gelten.
Erster Fall: Die höchste Potenz im Zählerterm ist kleiner als die im Nennerterm (also $n<m$). Dann gilt: $\lim\limits_{x\to\infty}f(x)=0$.
Zweiter Fall: Die höchste Potenz im Zählerterm ist gleich der im Nennerterm (also $n=m$). Dann gilt: $\lim\limits_{x\to\infty}f(x)=\frac{a_n}{b_m}$, der Quotient der beiden höchsten Koeffizienten.
Dritter Fall: Die höchste Potenz im Zählerterm ist größer als die im Nennerterm (also $n>m$). Dann gilt: $\lim\limits_{x\to\infty}f(x)=\pm\infty$.
Wie kommst du zu dem Vorzeichen? Betrachte die Vorzeichen von $a_n$ sowie $b_m$. Sind beide identisch, ist der Grenzwert $+\infty$ und andernfalls $-\infty$.
-
Ermittle jeweils den Grenzwert der Funktion.
TippsGanzrationale Funktionen streben für $x\to\infty$ beziehungsweise $x\to-\infty$ immer gegen $+\infty$ oder $-\infty$.
Die allgemeine Form einer gebrochenrationalen Funktion $f$ sei:
$f(x)=\frac{a_nx^n+...+a_1x+a_0}{b_mx^m+...+b_1x+b_0}$, $a_n\neq 0$ sowie $b_m\neq0$
Du unterscheidest für das Verhalten im Unendlichen folgende Fälle:
- $n<m$, dann gilt $\lim\limits_{x\to\infty}f(x)=0$
- $n=m$, dann gilt $\lim\limits_{x\to\infty}f(x)=\frac{a_n}{b_m}$
- $n>m$, dann gilt $\lim\limits_{x\to\infty}f(x)=\pm\infty$
Falls $n>m$ ist, entscheidest du das Vorzeichen des Grenzwertes wie folgt: Schau dir die Vorzeichen von $a_n$ sowie $b_m$ an. Sind beide identisch, ist der Grenzwert $+\infty$ und andernfalls $-\infty$.
LösungZunächst schauen wir uns die beiden Beispiele der ganzrationalen Funktionen an. Hier ist jeweils die höchste Potenz und der zugehörige Koeffizient ausschlaggebend.
Beispiel 1: $f(x)=\frac12x^4-x^2+3x-234$
- Die höchste Potenz ist $x^4$ mit einem geraden Exponenten $4$.
- Der zugehörige Koeffizient ist $\frac12>0$.
Beispiel 2: $f(x)=-3x^7+5x^5+3x^2-13,5x$
- Die höchste Potenz ist $x^7$ mit einem ungeraden Exponenten $7$.
- Der zugehörige Koeffizient ist $-3<0$.
Kommen wir nun zu zwei weiteren Beispielen. Dieses Mal schauen wir uns gebrochenrationale Funktionen an.
Beispiel 3: $f(x)=\dfrac{5x^2+2x-8}{-x^2-27356x+12345}$
Die höchste Potenz des Zählerterms ist $x^2$ und die des Nennerterms ebenfalls. Das bedeutet, dass die Funktion gegen den Quotienten der zugehörigen Koeffizienten geht:
$\lim\limits_{x\to\infty}f(x)=\frac{5}{-1}=-5$
Beispiel 4: $f(x)=\dfrac{-x^3+2x^4+10x}{0,5x^5-20x^4+x^3}$
Die höchste Potenz des Zählerterms ist $x^4$ und die des Nennerterms $x^5$. Da die Potenz des Nennerterms größer ist als die des Zählerterms, folgt:
$\lim\limits_{x\to\infty}f(x)=0$
-
Bestimme den höchsten Exponenten im Zähler- sowie im Nennerterm.
TippsBeachte: Üblicherweise werden bei ganzrationalen Funktionen die Potenzen der Größe nach geordnet. Dann steht die größte Potenz ganz links.
Dies ist in den angegebenen Beispielen nicht der Fall.
Schau dir ein Beispiel an. Die Funktion $f$ mit $f(x)=3x-4x^2+2x^7$ hat die höchste Potenz $x^7$.
Die höchste Potenz ist eindeutig. Du erkennst sie an dem größten Exponenten.
Zum Beispiel ist $x^5$ eine größere Potenz als $x^2$, da $5>2$ ist.
LösungWenn du eine ganzrationale Funktion auf ihr Verhalten im Unendlichen untersuchen willst, musst du dir zunächst die höchste Potenz anschauen. Dann kannst du den entsprechenden Grenzwert gemäß der dargestellten Tabelle bestimmen.
Eine Potenz hat die Form $x^n$. Dabei spricht man von der höchsten Potenz, wenn der Exponent, also $n$, am größten ist.
Schauen wir uns einmal zwei Beispiele dazu an:
- Die höchste Potenz von $f(x)=2x^3-x^5+x-8+3x^8$ ist $x^8$.
- Die höchste Potenz von $f(x)=2x^4+3-7x^5$ ist $x^5$.
-
Leite den Grenzwert der gebrochenrationalen Funktionenschar in Abhängigkeit von Parameterwerten her.
TippsSchreibe für die jeweils gegebenen Parameter den Funktionsterm auf.
In dem ersten und zweiten Fall ist die höchste Potenz im Zählerterm sowie im Nennerterm gleich groß.
Der Grenzwert ergibt sich als Quotient der zugehörigen Koeffizienten.
- Wenn die höchste Potenz im Zählerterm größer ist als die im Nennerterm, geht die gebrochenrationale Funktion gegen $\pm\infty$.
- Wenn die höchste Potenz im Zählerterm kleiner ist als die im Nennerterm, geht die gebrochenrationale Funktion gegen $0$.
LösungJe nachdem, wie die Parameter $a$ und $b$ gewählt werden, können die Funktionen dieser Schar im Grenzwertverhalten verschieden sein.
Erster Fall: $a\in\mathbb{R}$, $a\neq 0$ sowie $b\in\mathbb{R}$
Die höchste Potenz im Zähler- wie im Nennerterm ist $x^2$. Dann kann der Grenzwert wie folgt berechnet werden:
$\lim\limits_{x\to\infty}\left(\dfrac{ax^2+bx+3}{2ax^2+x}\right)=\dfrac{a}{2a}=\dfrac12$
Zweiter Fall: $a=0$ und $b\in\mathbb{R}$, $b\neq 0$
Dieses Mal ist $f_{0;b}(x)=\dfrac{bx+3}{x}$. Die höchste Potenz im Zähler- wie im Nennerterm ist jeweils $x$. Du kannst nun den Grenzwert wieder als Quotient der zugehörigen Koeffizienten berechnen:
$\lim\limits_{x\to\infty}\left(\dfrac{bx+3}{x}\right)=\dfrac{b}{1}=b$
Dritter Fall: $a=b=0$
Es ist $f_{0;0}(x)=\dfrac{3}{x}$. Da die höchste Potenz im Zählerterm kleiner ist als die im Nennerterm, gilt:
$\lim\limits_{x\to\infty}\left(\frac{3}{x}\right)=0$
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Primzahlen
- Geometrische Lagebeziehungen
- Rechteck
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Quadrat
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Was Ist Eine Viertelstunde
- Prisma
- Mitternachtsformel
- Grundrechenarten Begriffe
- Dreiecksarten
- Quader
- Satz Des Pythagoras
- Dreieck Grundschule
- Erste Binomische Formel
- Kreis
- Standardabweichung
- Flächeninhalt
- Volumen Kugel
- Zahlen In Worten Schreiben
- Meter
- Orthogonalität
- Schriftlich Multiplizieren
- Brüche Multiplizieren
- Potenzgesetze
- Distributivgesetz
- Flächeninhalt Dreieck
- Rationale Zahlen
- Volumen Berechnen
- Brüche Addieren
- Kongruenz
- Exponentialfunktion
- Scheitelpunktform
- Logarithmus
- Erwartungswert
- Skalarprodukt
- Primfaktorzerlegung
- Quadratische Ergänzung
- Zinseszins
- Geradengleichung Aus Zwei Punkten Bestimmen
- Sinusfunktion
 Du möchtest schneller & einfacher lernen?
Du möchtest schneller & einfacher lernen?


 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen