Gegenseitige Lage Gerade-Gerade
In der Geometrie untersuchst du unter anderem Geraden sowie deren Lagebeziehungen zueinander. Hier lernst du, wie eine Geradengleichung aussieht und wie du die verschiedenen Lagen untersuchen kannst.
Beliebteste Videos
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Geradengleichungen im Raum
- Allgemeines Vorgehen
- Identische Geraden
- Parallele Geraden
- Sich schneidende Geraden
- Windschiefe Geraden
Geradengleichungen im Raum
Geraden im Raum sind entweder durch einen Punkt und einen Vektor oder durch zwei Punkte gegeben. Eine Parametergleichung sieht so aus:
$g:\vec x=\vec a+r\cdot \vec u$
Dabei ist
- $\vec x$ ein Vektor, der auf einen beliebigen Punkt der Geraden zeigt,
- $\vec a$ ein Vektor, der auf einen gegebenen Punkt der Geraden zeigt, der Stützvektor,
- $\vec u$ der Richtungsvektor und
- $r\in\mathbb{R}$ ein Parameter.
Allgemeines Vorgehen
Wenn zwei Geraden gegeben sind, untersuchst du zunächst die beiden Richtungsvektoren auf Kollinearität. Zwei Vektoren sind kollinear zueinander, wenn sich der eine Vektor als Vielfaches des anderen schreiben lässt.
Die Richtungsvektoren sind kollinear
In diesem Fall sind die Geraden entweder identisch oder parallel zueinander.
Wie kannst du diese beiden Fälle unterscheiden? Parallele Geraden haben keine gemeinsamen Punkte, identische Geraden haben unendlich viele gemeinsame Punkte.
Liegt also der Punkt, auf welchen der Stützvektor einer der beiden Geraden zeigt, auch auf der anderen Geraden, dann sind die Geraden identisch. Um zu überprüfen, ob ein Punkt auf einer Geraden liegt, führst du eine Punktprobe durch.
Die Richtungsvektoren sind nicht kollinear
In diesem Fall schneiden sich die Geraden entweder oder sind windschief zueinander.
Du musst ein lineares Gleichungssystem lösen, welches du durch Gleichsetzen der Geradengleichungen erhältst. Ist dieses Gleichungssystem lösbar, dann schneiden sich die Geraden. Anderenfalls sind sie windschief.
Nun wirst du jeweils an einem Beispiel sehen, wie du die gegenseitige Lage zweier Geraden untersuchst.
Identische Geraden
Gegeben sind die beiden Geraden
$g:\vec x=\begin{pmatrix} 1 \\\ 3 \\\ 2 \end{pmatrix}+r\cdot \begin{pmatrix} 1 \\\ 1 \\\ 2 \end{pmatrix}$
sowie
$h:\vec x=\begin{pmatrix} 5 \\\ 7 \\\ 10 \end{pmatrix}+s\cdot \begin{pmatrix} 3 \\\ 3 \\\ 6 \end{pmatrix}$
Die Richtungsvektoren, diese erkennst du daran, dass sie mit dem Parameter multipliziert werden, sind kollinear. Prüfe nun, ob der Punkt $P(5|7|10)$ auf der Geraden $g$ liegt. Für $r=4$ erhältst du den Ortsvektor dieses Punktes. Das bedeutet, dass der Punkt auch auf der Geraden $g$ liegt. Schließlich sind die beiden Geraden identisch.
Parallele Geraden
Dieses Mal schauen wir uns die beiden folgenden Geraden an:
$g:\vec x=\begin{pmatrix} 1 \\\ 3 \\\ 2 \end{pmatrix}+r\cdot \begin{pmatrix} 1 \\\ 1 \\\ 2 \end{pmatrix}$
sowie
$h:\vec x=\begin{pmatrix} 1 \\\ 2 \\\ 3 \end{pmatrix}+s\cdot \begin{pmatrix} 3 \\\ 3 \\\ 6 \end{pmatrix}$
Wieder sind die Richtungsvektoren kollinear. Die Punktprobe, ob $P(1|2|3)$ auf der Geraden $g$ liegt, führt zu einem Widerspruch. Das bedeutet, dass der Punkt nicht auf der Geraden $g$ liegt. Die Geraden sind somit parallel zueinander.
Außerdem kannst du noch den Abstand zwischen parallelen Geraden berechnen.
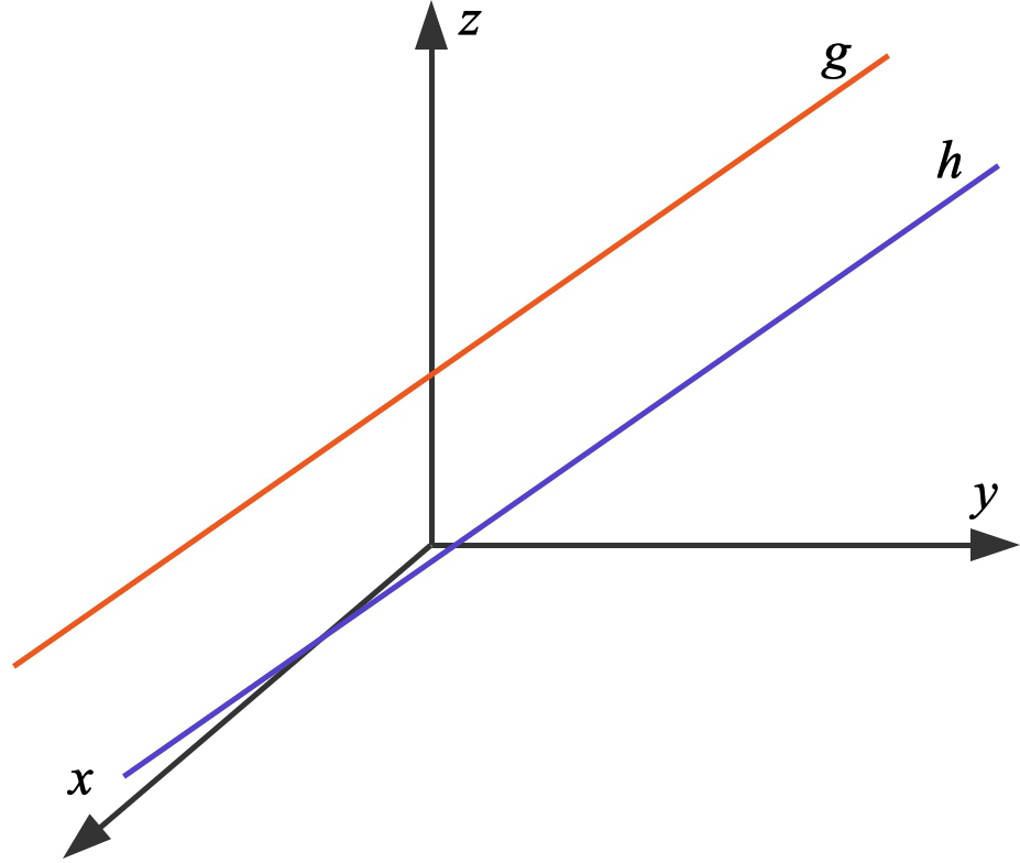
Nun bleiben noch die beiden Fälle, in welchen die Richtungsvektoren der betrachteten Geraden nicht kollinear sind.
Sich schneidende Geraden
Betrachte die folgenden Geraden:
$g:\vec x=\begin{pmatrix} 1 \\\ 3 \\\ 2 \end{pmatrix}+r\cdot \begin{pmatrix} 1 \\\ 1 \\\ 2 \end{pmatrix}$
sowie
$h:\vec x=\begin{pmatrix} 6 \\\ 5 \\\ 7 \end{pmatrix}+s\cdot \begin{pmatrix} -1 \\\ 2 \\\ 3 \end{pmatrix}$
Die beiden Richtungsvektoren sind nicht kollinear. Du musst nun das folgende lineare Gleichungssystem lösen:
$\begin{array}{lcccc} \text{(I)}&1+r&=&6-s\\ \text{(II)}&3+r&=&5+2s\\ \text{(III)}&2+2r&=&7+3s \end{array}$
- Wenn du von der zweiten Gleichung die erste subtrahierst, erhältst du $2=-1+3s$. Addiere nun $1$ und dividiere anschließend durch $3$, dann erhältst du $s=1$.
- Setze $s=1$ in die erste Gleichung ein. So erhältst du $r=4$.
- $s=1$ und $r=4$ erfüllen auch die dritte Gleichung.
Die beiden Geraden schneiden sich. Den Schnittpunkt erhältst du, indem du einen der beiden Parameter in die entsprechende Geradengleichung einsetzt. So kommst du zu $S(5|7|10)$.
Hier siehst du zwei sich schneidende Geraden:
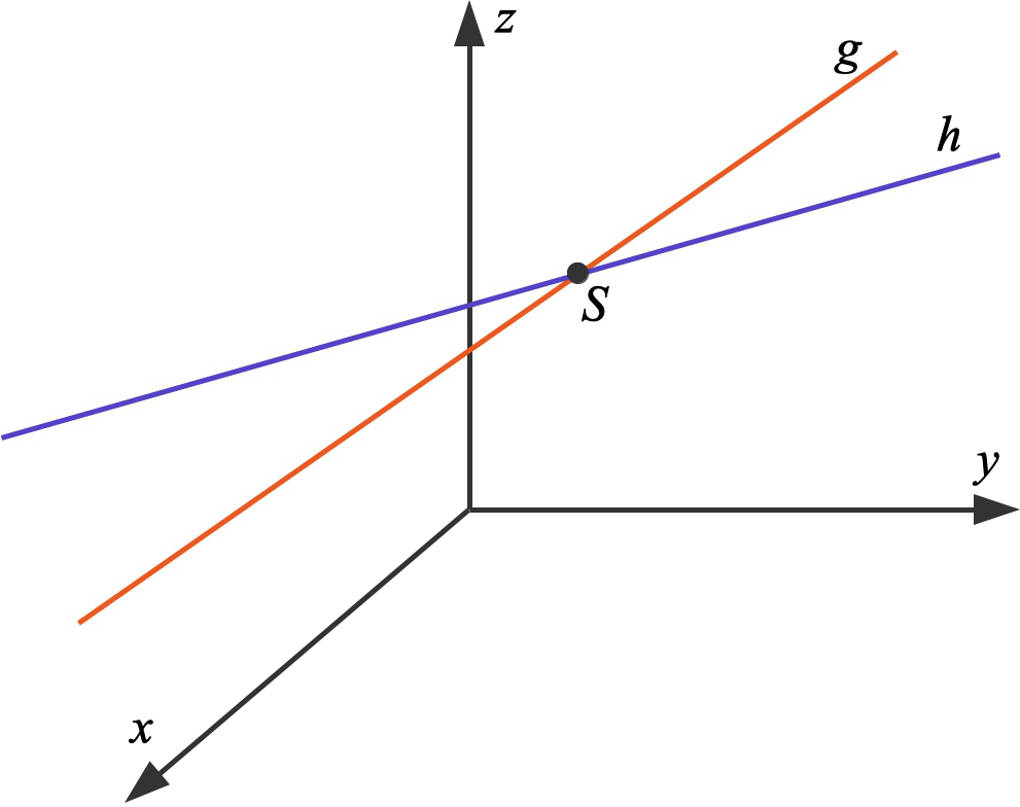
Zusätzlich zu dem Schnittpunkt kannst du auch noch den Schnittwinkel berechnen. Hierfür verwendest du die folgende Formel:
$\cos(\alpha)=\dfrac{|\vec u\cdot \vec v|}{|\vec u|\cdot |\vec v|}$
Dabei sind $\vec u$ sowie $\vec v$ die Richtungsvektoren der beiden Geraden.
Windschiefe Geraden
Nun bleibt noch der Fall windschiefer Geraden:
$g:\vec x=\begin{pmatrix} 1 \\\ 3 \\\ 2 \end{pmatrix}+r\cdot \begin{pmatrix} 1 \\\ 1 \\\ 2 \end{pmatrix}$
sowie
$h:\vec x=\begin{pmatrix} 6 \\\ 5 \\\ 5 \end{pmatrix}+s\cdot \begin{pmatrix} -1 \\\ 2 \\\ 3 \end{pmatrix}$
Wieder stellst du ein lineares Gleichungssystem auf:
$\begin{array}{lcccc} \text{(I)}&1+r&=&6-s\\ \text{(II)}&3+r&=&5+2s\\ \text{(III)}&2+2r&=&5+3s \end{array}$
Auch hier führen die ersten beiden Gleichungen zu $r=4$ sowie $s=1$.
Setze diese in die dritte Gleichung ein: Du erhältst dann $2+2\cdot 4=10$ auf der linken Seite sowie $5+3\cdot 1=8$ auf der rechten Seite und demnach einen Widerspruch. Das bedeutet schließlich, dass das lineare Gleichungssystem nicht lösbar ist.
Die beiden Geraden sind windschief.
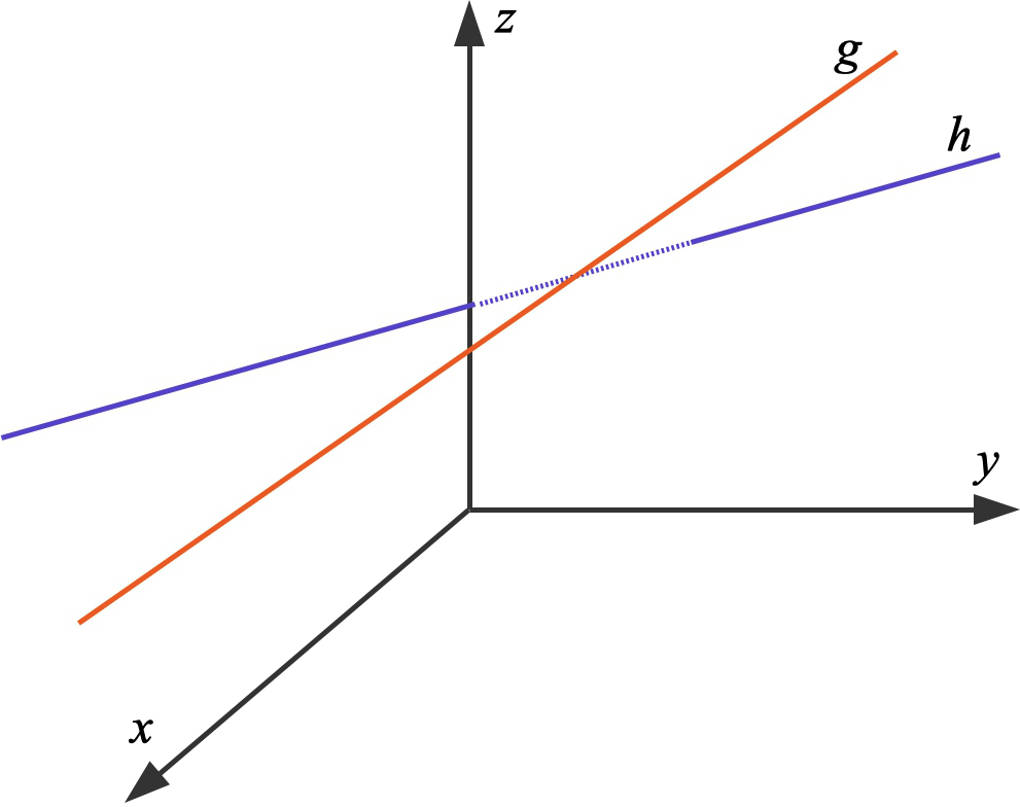
Bei windschiefen Geraden kannst du noch den Abstand dieser Geraden zueinander berechnen.
Alle Videos zum Thema
Videos zum Thema
Gegenseitige Lage Gerade-Gerade (7 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Gegenseitige Lage Gerade-Gerade (7 Arbeitsblätter)
-
 Gegenseitige Lage Gerade-Gerade
PDF anzeigen
Gegenseitige Lage Gerade-Gerade
PDF anzeigen -
 Gegenseitige Lage Gerade-Gerade – Beispiele
PDF anzeigen
Gegenseitige Lage Gerade-Gerade – Beispiele
PDF anzeigen -
 Lagebeziehungen im Raum – Beispiel Flugbahnen
PDF anzeigen
Lagebeziehungen im Raum – Beispiel Flugbahnen
PDF anzeigen -
 Lagebeziehungen im Raum – Beispiel Flugzeugkollision
PDF anzeigen
Lagebeziehungen im Raum – Beispiel Flugzeugkollision
PDF anzeigen -
 Lagebeziehungen im Raum – Flugzeugaufgabe
PDF anzeigen
Lagebeziehungen im Raum – Flugzeugaufgabe
PDF anzeigen -
 Oktaeder im Raum – Oberflächeninhalt und Volumen
PDF anzeigen
Oktaeder im Raum – Oberflächeninhalt und Volumen
PDF anzeigen -
 Lagebeziehungen von zwei Geraden im Raum
PDF anzeigen
Lagebeziehungen von zwei Geraden im Raum
PDF anzeigen
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Primzahlen
- Geometrische Lagebeziehungen
- Rechteck
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Quadrat
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Was Ist Eine Viertelstunde
- Prisma
- Mitternachtsformel
- Grundrechenarten Begriffe
- Dreiecksarten
- Quader
- Satz Des Pythagoras
- Dreieck Grundschule
- Erste Binomische Formel
- Kreis
- Standardabweichung
- Flächeninhalt
- Volumen Kugel
- Zahlen In Worten Schreiben
- Meter
- Orthogonalität
- Schriftlich Multiplizieren
- Brüche Multiplizieren
- Potenzgesetze
- Distributivgesetz
- Flächeninhalt Dreieck
- Rationale Zahlen
- Volumen Berechnen
- Brüche Addieren
- Kongruenz
- Exponentialfunktion
- Scheitelpunktform
- Logarithmus
- Erwartungswert
- Skalarprodukt
- Primfaktorzerlegung
- Quadratische Ergänzung
- Zinseszins
- Geradengleichung Aus Zwei Punkten Bestimmen
- Sinusfunktion




















