Seiten und Winkel von Dreiecken
Hast du schon einmal die Innenwinkel eines Dreiecks gemessen? Ist dir dabei auch aufgefallen, dass die Summe dieser drei Innenwinkel 180 Grad beträgt? Dies ist bei jedem Dreieck der Fall..
Beliebteste Videos
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
Winkel
Um diesen Text zu lesen, solltest du bereits wissen, was ein Winkel ist. Hier lernst du Winkelsummen in Dreiecken, in Vierecken und in Vielecken kennen.
Die Winkelsumme in Dreiecken
Ein Dreieck ist eine ebene Figur. Hier siehst du die Skizze eines Dreiecks:

- Es zeichnet sich (wie schon der Name sagt) dadurch aus, dass es drei Eckpunkte hat. Diese werden gegen den Uhrzeigersinn mit den Großbuchstaben $A$, $B$ und $C$ beschriftet. Die drei Eckpunkte werden durch Strecken verbunden.
- Die Strecken werden auch Seiten genannt und üblicherweise mit Kleinbuchstaben entsprechend dem gegenüberliegenden Eckpunkt bezeichnet.
- Jeder der Eckpunkte ist der Scheitel eines Winkels. Die Innenwinkel eines Dreiecks werden mit den griechischen Kleinbuchstaben $\alpha$ (alpha), $\beta$ (beta) und $\gamma$ (gamma) beschriftet.
Der Winkelsummensatz
In jedem beliebigen Dreieck gilt der Winkelsummensatz:
$\alpha+\beta+\gamma=180^\circ$
Begründung des Winkelsummensatzes
Wir betrachten noch einmal das obige Dreieck. Zur besseren Lesbarkeit sind nur noch die Winkel beschriftet. Du erkennst in dem Bild eine gestrichelte Linie parallel zu der blauen Seite. So erhältst du zwei Winkel $\delta$ und $\epsilon$.

- Die drei Winkel $\delta$, $\gamma$ und $\epsilon$ ergänzen sich zu $180^\circ$. Einen solchen Winkel nennt man auch gestreckter Winkel.
- Die Winkel $\alpha$ und $\delta$ sowie $\beta$ und $\epsilon$ sind Wechselwinkel. Da Wechselwinkel gleich groß sind, folgt damit $\alpha =\delta$ sowie $\beta =\epsilon$.
Insgesamt kannst du daraus folgern, dass die Summe der Innenwinkel in einem Dreieck $\alpha+\beta+\gamma=180^\circ$ ergibt.
Rechtwinkliges Dreieck
In einem rechtwinkligen Dreieck ist einer der drei Winkel ein rechter Winkel. Dieser hat den Wert $90^\circ$. Das bedeutet, dass die beiden anderen Winkel zusammen ebenfalls $90^\circ$ ergeben müssen. Sei zum Beispiel $\gamma=90^\circ$, dann gilt $\alpha+\beta=90^\circ$. Die beiden Winkel sind somit spitze Winkel.
Gleichseitiges Dreieck
In einem gleichseitigen Dreieck sind alle drei Seiten gleich lang. Damit sind auch alle Winkel gleich groß. Das bedeutet, es gilt $\alpha=\beta=\gamma$. Daraus kannst du folgern, dass $3\alpha=180^\circ$ ist. Eine Division durch $3$ auf beiden Seiten der Gleichung führt zu $\alpha=60^\circ$.
In einem gleichseitigen Dreieck betragen also alle drei Winkel $60^\circ$.
Exkurs: Die Winkelsumme in Vielecken
Nun kannst du dich natürlich fragen, ob es auch Aussagen über die Winkelsummen von Vielecken mit mehr als drei Ecken gilt.
Die Winkelsumme von Vierecken
Dies schauen wir uns einmal am Beispiel eines Quadrates an.

Die blaue Diagonale teilt das Quadrat in zwei kongruente, rechtwinklige Dreiecke. Für jedes dieser Dreiecke gilt der Winkelsummensatz. Das bedeutet, dass sich in beiden Dreiecken die drei Innenwinkel zu $180^\circ$ summieren. Da das Quadrat aus zwei Dreiecken „besteht“, gilt, dass sich die vier Innenwinkel in dem Quadrat zu $2\cdot 180^\circ=360^\circ$ summieren.
Für jedes beliebige Viereck gilt:
$\alpha+\beta+\gamma+\delta=360^\circ$
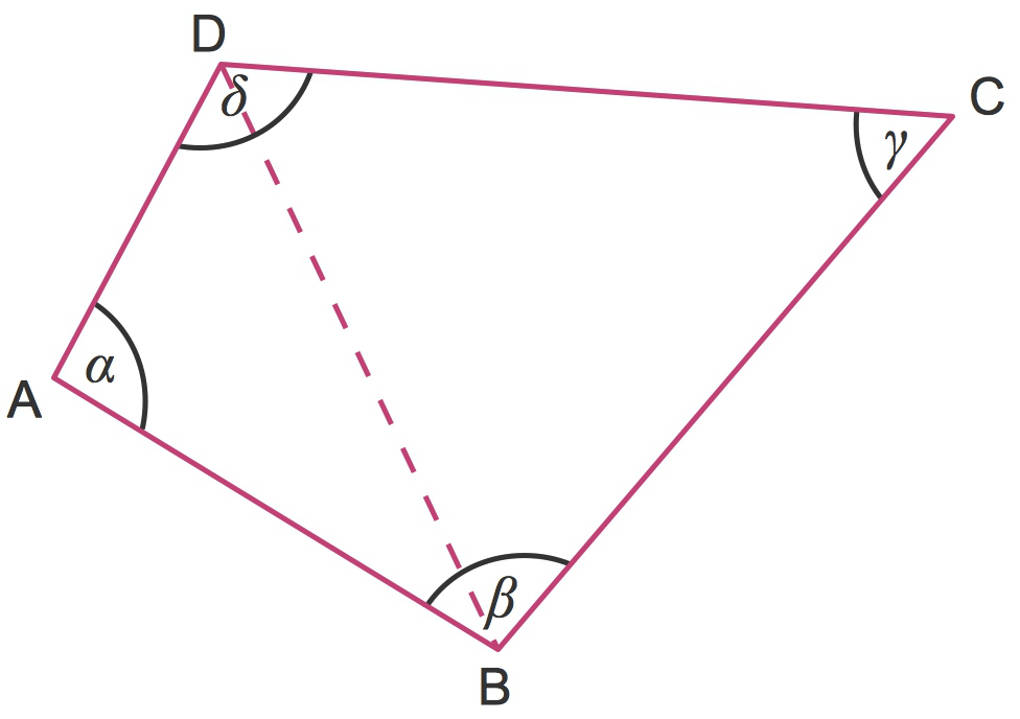
Die eingezeichnete Diagonale teilt das Viereck in zwei Dreiecke. So kannst du in jedem beliebigen Viereck die Summe der vier Innenwinkel bestimmen.
Die Winkelsumme eines Fünfecks
Hier siehst du ein in einen Kreis eingeschriebenes regelmäßiges Fünfeck.

Dieses Fünfeck kannst du in fünf kongruente, gleichschenklige Dreiecke unterteilen.
- Jedes dieser Dreiecke hat einen $72^\circ$-Winkel. Auf diesen kommst du, wenn du den Vollwinkel $(360^\circ)$ durch $5$ teilst.
- Die gleich großen Basiswinkel betragen jeweils $\frac{180^\circ-72^\circ}2=54^\circ$.
- Nun kannst du zählen, wie viele dieser Winkel sich in dem Fünfeck befinden: Es sind $10$. Somit beträgt die Summe der fünf Innenwinkel $10\cdot 54^\circ=540^\circ$. Auch dies gilt für jedes beliebige Fünfeck.
Die Winkelsumme eines beliebigen Vielecks
In einem beliebigen $n$-Eck gilt der folgende Winkelsummensatz:
Die Summe der $n$ Innenwinkel eines $n$-Ecks beträgt $(n-2)\cdot 180^\circ$.
Umgekehrt kannst du auch bei bekannter Winkelsumme die Anzahl der Ecken berechnen:
Wie viele Ecken hat bspw. ein Vieleck mit der Winkelsumme $1980^\circ$?
Es muss gelten $(n-2)\cdot 180^\circ=1980^\circ$. Teile auf beiden Seiten durch $180^\circ$. Du erhältst $n-2=11$. Hier kannst du nun noch $2$ addieren. Das ergibt $n=11+2=13\text{.}$
Ein Vieleck mit einer Innenwinkelsumme von $1980^\circ$ hat also $13$ Ecken.
Alle Videos zum Thema
Videos zum Thema
Seiten und Winkel von Dreiecken (5 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Seiten und Winkel von Dreiecken (5 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Primzahlen
- Geometrische Lagebeziehungen
- Rechteck
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Quadrat
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Was Ist Eine Viertelstunde
- Prisma
- Mitternachtsformel
- Grundrechenarten Begriffe
- Dreiecksarten
- Quader
- Satz Des Pythagoras
- Dreieck Grundschule
- Erste Binomische Formel
- Kreis
- Standardabweichung
- Flächeninhalt
- Volumen Kugel
- Zahlen In Worten Schreiben
- Meter
- Orthogonalität
- Schriftlich Multiplizieren
- Brüche Multiplizieren
- Potenzgesetze
- Distributivgesetz
- Flächeninhalt Dreieck
- Rationale Zahlen
- Volumen Berechnen
- Brüche Addieren
- Kongruenz
- Exponentialfunktion
- Scheitelpunktform
- Logarithmus
- Erwartungswert
- Skalarprodukt
- Primfaktorzerlegung
- Quadratische Ergänzung
- Zinseszins
- Geradengleichung Aus Zwei Punkten Bestimmen
- Sinusfunktion









 Innenwinkelsummen von Dreiecken
Innenwinkelsummen von Dreiecken
 Innenwinkel und Außenwinkel von Dreiecken
Innenwinkel und Außenwinkel von Dreiecken
 Dreiecksungleichung – Erklärung
Dreiecksungleichung – Erklärung
 Basiswinkelsatz – Erklärung und Umkehrung
Basiswinkelsatz – Erklärung und Umkehrung
 Seiten und Winkel im Dreieck
Seiten und Winkel im Dreieck









