Proportionale und antiproportionale Zuordnungen
Durch Untersuchung einer Zuordnung auf Quotientengleichheit oder Produktgleichheit kann man ermitteln, ob es sich um eine proportionale oder antiproportionale Zuordnung handelt.
Beliebteste Videos
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Was ist eine Zuordnung?
- Proportionale Zuordnungen
- Quotientengleichheit
- Graphische Darstellung proportionaler Zuordnungen
- Anwendungsbeispiel: Klopapierrollen
- Anwendungsbeispiel: Fitness
- Anwendungsbeispiel: Hennenstreit
- Antiproportionale Zuordnungen
Was ist eine Zuordnung?
Eine Zuordnung ist eine Beziehung zwischen zwei Größen aus zwei Mengen, die über eine Zuordnungsvorschrift festgelegt ist.
Das bedeutet: Eine Zuordnung ordnet einem Wert einen anderen eindeutig zu.
Proportionale Zuordnungen
Es gibt verschiedene Arten der Darstellung von Zuordnungen. Beispiel: $30$ Liter Benzin kosten $45€$.
Diese Aussage ist eine Zuordnung zwischen Benzinmenge (Ausgangswert) und Preis (zugeordnetem Wert) und kann in einem Pfeildiagramm dargestellt werden:
Volumen (Liter) $\rightarrow$ Preis ($€$)
Anhand der zugehörigen Wertetabelle wird ersichtlich, dass es sich hier um eine proportionale Zuordnung handelt:

Die dritte Tabellenspalte (Rechnung) verdeutlicht nämlich, wie sich weitere Wertepaare berechnen lassen: Ausgangsgröße und zugeordnete Größe werden jeweils mit demselben Faktor multipliziert oder dividiert.
Allgemein bedeutet dies: Verdoppelt/verdreifacht/halbiert … sich der Ausgangswert, so verdoppelt/verdreifacht/halbiert … sich ebenfalls der zugeordnete Wert.
Quotientengleichheit
In der vierten Spalte der Wertetabelle erscheint der Quotient aus zugeordneter Größe und entsprechender Ausgangsgröße. Er weist einen gleichbleibenden Wert auf:
$\frac{\text{zugeordnete Größe}}{\text{Ausgangsgröße}} = \frac{\text{Preis}}{\text{Volumen}} = 1,5\ \frac{\text{Euro}}{\text{Liter}}=\text{konstanter Wert}$
Diese Eigenschaft nennt man Quotientengleichheit. Sie kann genutzt werden, um zu überprüfen, ob es sich bei einer Zuordnung um eine proportionale Zuordnung handelt. Wenn man den konstanten Wert kennt, kann damit auch die zugeordnete Größe berechnet werden:
$\text{zugeordnete Gr}\ddot{\text{o}}\text{ße} = \text{konstanter Wert} \cdot \text{Ausgangs}\ddot{\text{o}}\text{ße}$
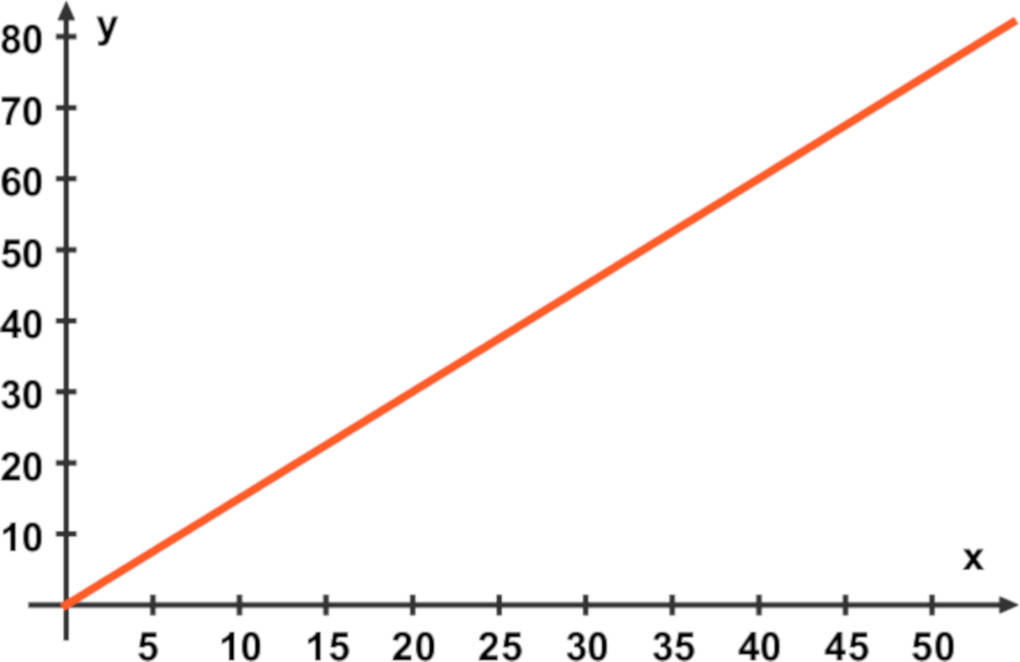
Graphische Darstellung proportionaler Zuordnungen
Eine Zuordnung lässt sich grafisch in einem Koordinatensystem darstellen. Dabei wird die Skala für die Ausgangsgröße auf der $x$-Achse abgetragen und die Skala für die zugeordnete Größe auf $y$-Achse.
Im obigen Beispiel bezeichnet also die $x$-Achse das Volumen und die $y$-Achse den Preis. Die Wertepaare $($ Volumen $\vert $ Preis$)$ werden als Punkte in das Koordinatensystem eingetragen:
$\begin{array}{lllllllllll} (5 | 7,50) ; && (10 |15) ; && (15 | 22,50) ; && (30 | 45) ; && (60 | 90) ; && (90 | 135) \end{array}$
Verbindet man die Punkte miteinander, so liegen sie auf einer Halbgeraden, die im Punkt $(0 | 0)$ beginnt.
Anwendungsbeispiel: Klopapierrollen
Was macht Frau Schmidt denn nur mit so viel Klopapier? Sie hat $5$ Pakete in ihrem Einkaufswagen und trifft an der Kasse auf Frau Müller. Sie hat bereits $7$ Pakete auf das Band gelegt, diese $7$ Pakete beinhalten $56$ Rollen.

Wie viele Rollen Klopapier kauft Frau Schmidt? Die Berechnung erfolgt in folgender Tabelle mit Hilfe eines Dreisatzes:

In den $5$ Paketen befinden sich $40$ Rollen.
Anwendungsbeispiel: Fitness
Frau Schlappner hat auf ihrem Heimtrainer bereits $96$ Umdrehungen zurückgelegt, das entspricht einer Strecke von $800\ \text{m}$.

Sie möchte gerne $5\ \text{km}$ schaffen. Wie viele Umdrehungen wären das? Wieder wird die gesuchte Anzahl wie folgt mit Hilfe des Dreisatzes berechnet:
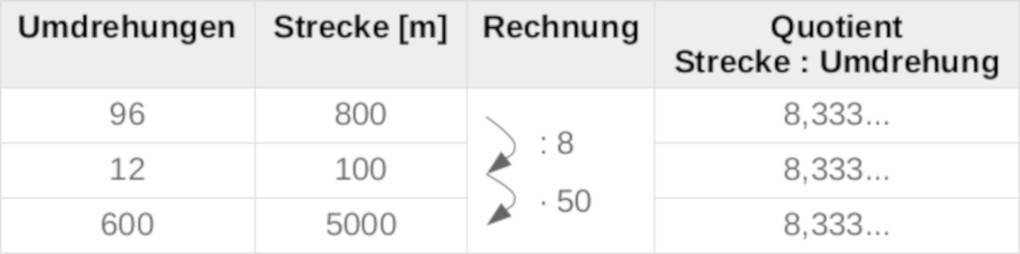
$5\ \text{km}$ auf dem Heimtrainer entsprechen $600$ Umdrehungen.
Anwendungsbeispiel: Hennenstreit
Berta und Emma wetteifern, wer die beste Legehenne ist. Berta kann in $24$ Tagen $30$ Eier legen, Emma schafft in $35$ Tagen $49$ Eier.
Welche der beiden Hennen wird gewinnen, wenn ein Zeitraum von $100$ Tagen gewählt wird? Wie gehen wie folgt vor:
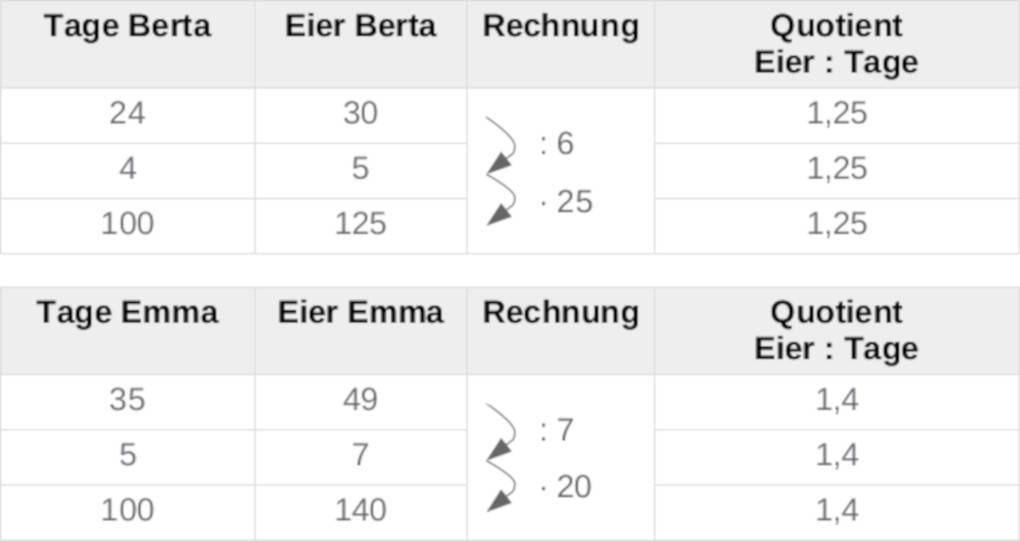
Emma ist besser, sie legt $15$ Eier mehr als Berta.
Antiproportionale Zuordnungen
Bei einer antiproportionalen Zuordnung oder auch umgekehrt proportionalen Zuordnung gilt: Zu dem Doppelten/Dreifachen/der Hälfte ... der Ausgangsgröße gehört die Hälfte/ein Drittel/das Doppelte ... der zugeordneten Größe.
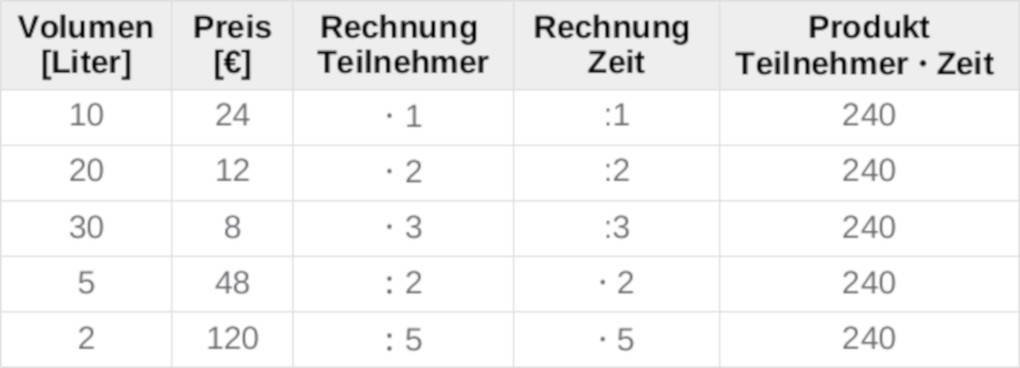
Beispiel: Der Lebensmittelvorrat im Basislager einer Himalaja-Expedition reicht bei $10$ Teilnehmern $24$ Tage. Wie lange reicht derselbe Vorrat bei $20$ oder $30$ Teilnehmern? Wie lange reicht er bei $5$ oder gar nur $2$ Teilnehmern?
Bei diesem Beispiel wird vorausgesetzt, dass jedes Mitglied der Expedition jeden Tag gleich viele Lebensmittel verbraucht. Dann reicht der Vorrat für $20$ Teilnehmer nur halb so lange wie für $10$ Teilnehmer und für $5$ Teilnehmer doppelt so lange wie für $10$ Teilnehmer.
Die Ausgangsgröße ist die Anzahl der Teilnehmer und die zugeordnete Größe die Zeit in Tagen, dann erhält man folgendes Pfeildiagramm:
Teilnehmer (Anzahl) $\rightarrow$ Zeit (Tage)
In der Wertetabelle muss im Unterschied zur proportionalen Zuordnung auf der rechten Seite immer die Gegenoperation zu der Operation auf der linken Seite durchgeführt werden.
Dies wird in der dritten und vierten Spalte der Wertetabelle ersichtlich:
Produktgleichheit
Wenn man bei einer antiproportionalen Zuordnung die Ausgangsgröße und die zugeordnete Größe multipliziert, erhält man stets denselben Wert:
$\text{Ausgangsgr}\ddot{\text{o}}\text{ße} \cdot \text{zugeordnete Gr}\ddot{\text{o}}\text{ße} = \text{konstanter Wert}$
Im Expeditionsbeispiel ist es der Wert $240$.
Diese Eigenschaft nennt man Produktgleichheit: Man kann sie nutzen, um zu überprüfen, ob es sich um eine antiproportionale Zuordnung handelt. Wenn der konstante Wert bekannt ist, kann damit du auch die zugeordnete Größe bestimmt werden:
$\text{zugeordnete Gr}\ddot{\text{o}}\text{ße} = \text{konstanter Wert} : \text{Ausgangsgr}\ddot{\text{o}}\text{ße}$
Graphische Darstellung antiproportionaler Zuordnungen
Auch antiproportionale Zuordnungen können im Koordinatensystem veranschaulicht werden. Die Skala für die Ausgangsgröße wird wieder auf der $x$-Achse abgetragen und die Skala für die zugeordnete Größe auf der $y$-Achse.
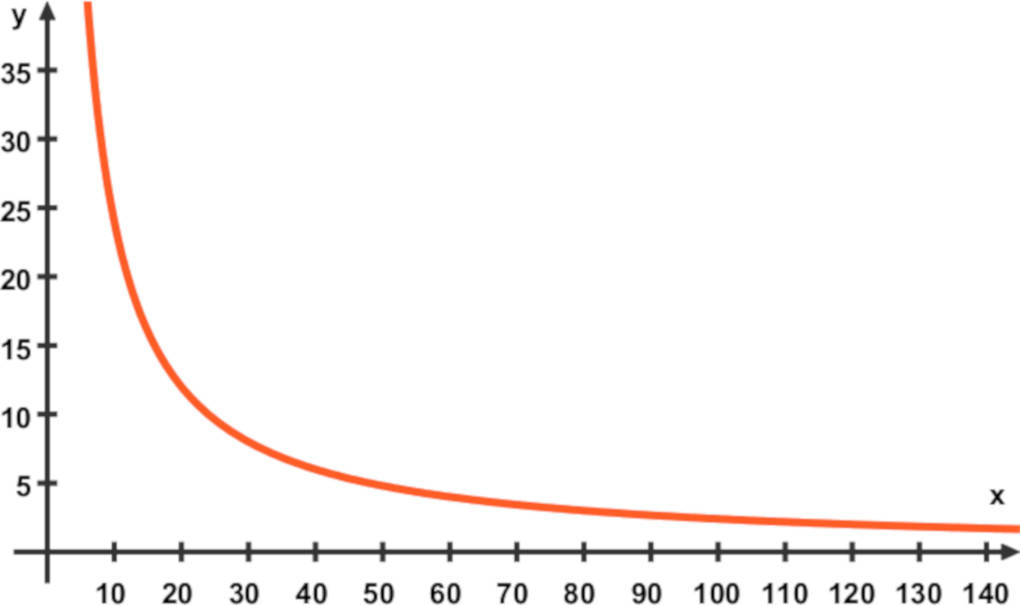
Die Punkte des Graphen einer antiproportionalen Zuordnung liegen immer auf einer Kurve. Diese Kurve nennt man Hyperbel.
Anwendungsbeispiel: Klassenraum
In einer Klasse mit $24$ Schülern muss nach $10$ Minuten Unterricht gelüftet werden.

Nach wie vielen Minuten Unterricht muss ein Klassenzimmer mit $32$ Schülern gelüftet werden? Dieser antiproportionale Zusammenhang wird in folgender Tabelle mit Hilfe des Dreisatzes untersucht:

Man muss also bereits nach $7,5$ Minuten lüften.
Anwendungsbeispiel: Rechteck
Ein Rechteck hat die Länge $a = 20\ \text{cm}$ und die Breite $b = 9\ \text{cm}$.

Wie breit ist ein Rechteck mit gleichem Flächeninhalt, das $15\ \text{cm}$ lang ist?
Der Flächeninhalt eines Rechtecks entspricht dem Produkt seiner beiden Seitenlängen, also gilt $A=a\cdot b$. Demnach ist in dieser Aufgabe Produktgleichheit gefordert. Man rechnet wie folgt, um die neue Länge von $15\ \text{cm}$ zu erreichen:
$ 20\ \text{cm}:4\cdot 3=15\ \text{cm} $
Da es sich hier um eine antiproportionale Zuordnung handelt, muss die Breite $b=9\ \text{cm}$ mit $4$ multipliziert und durch $3$ geteilt werden. Es folgt also:
$ 9\ \text{cm}\cdot 4:3=12\ \text{cm} $
Das neue Rechteck hat also eine Breite von $12\ \text{cm}$.
Anwendungsbeispiel: Topf
Herr Vorsicht möchte Wasser aus einem großen Topf in einen kleineren umschütten. Der große Topf hat eine Grundfläche von $410\ \text{cm}^{2}$, die des kleinen Topfes beträgt $280 \ \text{cm}^{2}$.

Das Wasser im großen Topf hat einen Füllstand von $14\ \text{cm}$, der kleine Topf ist $20\ \text{cm}$ hoch. Klappt das Umfüllen?
Das Volumen eines Zylinders entspricht dem Produkt von Grundfläche und Höhe. Das Wasservolumen wird also wie folgt bestimmt:
$ V_{Wasser}=410\ \text{cm}^2\cdot 14\ \text{cm}=5740\ \text{cm}^3 $
Da sich das Volumen des Wassers beim Umschütten nicht ändert, liegt Produktgleichheit vor. Es folgt mit dem Dreisatz:
$ 410\ \text{cm}^2 :41\cdot 28=280\ \text{cm}^2 $
$ 14\ \text{cm} \cdot 41: 28= 20,5\ \text{cm} $
Nach dem Umfüllen würde das Wasser im kleinen Topf $20,5\ \text{cm}$ hoch stehen, es schwappt also über.
Alle Videos zum Thema
Videos zum Thema
Proportionale und antiproportionale Zuordnungen (11 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Proportionale und antiproportionale Zuordnungen (11 Arbeitsblätter)
-
 Proportionale Zuordnungen
PDF anzeigen
Proportionale Zuordnungen
PDF anzeigen -
 Antiproportionale Zuordnungen
PDF anzeigen
Antiproportionale Zuordnungen
PDF anzeigen -
 Proportionalitätsfaktor und Antiproportionalitätsfaktor
PDF anzeigen
Proportionalitätsfaktor und Antiproportionalitätsfaktor
PDF anzeigen -
 Direkte Proportionalität
PDF anzeigen
Direkte Proportionalität
PDF anzeigen -
 Von der Wertetabelle zur Gleichung
PDF anzeigen
Von der Wertetabelle zur Gleichung
PDF anzeigen -
 Graphen proportionaler Zuordnungen
PDF anzeigen
Graphen proportionaler Zuordnungen
PDF anzeigen -
 Proportionale Zuordnungen mit negativer Steigung
PDF anzeigen
Proportionale Zuordnungen mit negativer Steigung
PDF anzeigen -
 Proprotionale Zuordnungen vergleichen
PDF anzeigen
Proprotionale Zuordnungen vergleichen
PDF anzeigen -
 Proportionale Zuordnungen erkennen
PDF anzeigen
Proportionale Zuordnungen erkennen
PDF anzeigen -
 Antiproportionale Zuordnungen erkennen
PDF anzeigen
Antiproportionale Zuordnungen erkennen
PDF anzeigen -
 Antiproportionale Zuordnungen (Übungsvideo)
PDF anzeigen
Antiproportionale Zuordnungen (Übungsvideo)
PDF anzeigen
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Primzahlen
- Geometrische Lagebeziehungen
- Rechteck
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Quadrat
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Was Ist Eine Viertelstunde
- Prisma
- Mitternachtsformel
- Grundrechenarten Begriffe
- Dreiecksarten
- Quader
- Satz Des Pythagoras
- Dreieck Grundschule
- Erste Binomische Formel
- Kreis
- Standardabweichung
- Flächeninhalt
- Volumen Kugel
- Zahlen In Worten Schreiben
- Meter
- Orthogonalität
- Schriftlich Multiplizieren
- Brüche Multiplizieren
- Potenzgesetze
- Distributivgesetz
- Flächeninhalt Dreieck
- Rationale Zahlen
- Volumen Berechnen
- Brüche Addieren
- Kongruenz
- Exponentialfunktion
- Scheitelpunktform
- Logarithmus
- Erwartungswert
- Skalarprodukt
- Primfaktorzerlegung
- Quadratische Ergänzung
- Zinseszins
- Geradengleichung Aus Zwei Punkten Bestimmen
- Sinusfunktion
























