Quadratische Funktionen: f(x) = (x + d)²
Durch Variation eines Parameters kann der Graph einer quadratischen Funktion entlang der x-Achse verschoben werden.
Inhaltsverzeichnis zum Thema
- Was sind quadratische Funktionen?
- Die quadratische Funktion der Form $y=(x+d) ^2$
- Graphen von quadratischen Funktionen dieser Form
Was sind quadratische Funktionen?
Eine quadratische Funktion ist eine ganzrationale Funktion zweiten Grades. Da steckten aber viele mathematische Begriffe in einem Satz! Manchmal kann die Mathematik richtig zur eigenen Sprache werden. Du musst das Ganze nur Übersetzen:
Funktionen ordnen einer Zahl $x$ eine bestimmte Zahl $y$ zu. Die Funktionsvorschrift berechnet jeweils aus $x$ die Zahl $y$. Deshalb wird $x$ auch als Variable bezeichnet, denn sie kann gewählt werden. Der $y$-Wert ist davon abhängig.
So eine Funktionsgleichung könnte zum Beispiel so aussehen: $y=x^{2}$. Sie ordnet jeder Zahl $x$ sein Quadrat zu. Sie beschreibt den Zusammenhang zwischen den Seitenlängen $x$ von Quadraten und ihren dazugehörigen Flächen $y$. Deshalb werden Funktionen bei dem der höchste Exponent (Hochzahl) von $x$ genau $2$ ist quadratisch genannt. Das macht doch schon viel mehr Sinn!
Nur was sind denn nun ganzrationale Funktionen? Du kennst vielleicht die rationalen Zahlen. Das sind Zahlen, die als endlicher Bruch aufgeschrieben werden können. Und ganzrational bedeutet im Zusammenhang mit Funktionen, dass die Variable $x$ nicht im Nenner (unten im Bruch) stehen darf. Mit Grad misst man hier keine Winkel. Vielmehr ist der höchste Exponent von $x$ gemeint. Also zwei oder auch zweiten Grades.
Die Funktionsgleichung von oben $y=x^{2}$ ist die einfachste aller quadratischen Funktionen. Fast genauso einfach ist…
Die quadratische Funktion der Form $y=(x+d) ^2$
Da hat sich noch ein $d$ ins Quadrat geschlichen! Dieser wird auch Parameter genannt und ist ein Platzhalter für eine ganz normale Zahl. So eine Funktionsgleichung könnte zum Beispiel beschreiben, was mit der Fläche eines Quadrates passiert, wenn beide Seitenlängen $x$ um $d$ verlängert werden. Genauso könnte sie eine Verkürzung der Seitenlängen beschreiben, wenn $d$ negativ ist.
Graphen von quadratischen Funktionen dieser Form
Der Graph einer quadratischen Funktion wird Parabel genannt. Du kannst diese zum Beispiel mit einer Wertetabelle zeichnen. Für $y=x^{2}$ erhältst du als Graph die sog. Normalparabel. Ihr unterster Punkt liegt im Ursprung $O(0\vert 0)$. Er wird Scheitelpunkt genannt.
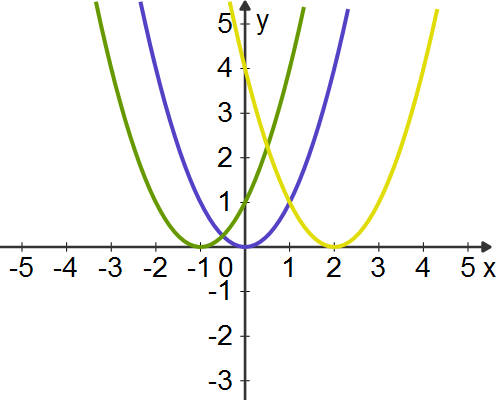
Der Parameter $d$ verschiebt den Scheitelpunkt und damit die ganze Parabel nur auf der $x$-Achse. Aber warum ist das so? Sieh dir dafür folgendes Beispiel an:
$y=(x-2)^2$
Die rechte Seite ist immer positiv, weil alle Zahlen im Quadrat positiv sind. Der kleinste $y$-Wert ist damit null und gleichzeitig die $y$-Koordinate des Scheitelpunkts. Wenn $y=0$ ist, dann muss $x=2$ sein. Weil dann die Klammer null wird und null mal null immer noch null ist! Die Parabel hat den Scheitelpunkt $S(2\vert 0)$.
Die Graphen solcher Parabeln könntest du sogar mit einer (selbstgebastelten) Parabelschablone zeichnen. Dabei legst du den unteren Punkt der Schablone auf den Scheitelpunkt und zeichnest dann an der Schablone entlang.
Alle Videos zum Thema
Videos zum Thema
Quadratische Funktionen: f(x) = (x + d)² (1 Video)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Quadratische Funktionen: f(x) = (x + d)² (1 Arbeitsblatt)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Primzahlen
- Geometrische Lagebeziehungen
- Rechteck
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Quadrat
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Was Ist Eine Viertelstunde
- Prisma
- Mitternachtsformel
- Grundrechenarten Begriffe
- Dreiecksarten
- Quader
- Satz Des Pythagoras
- Dreieck Grundschule
- Erste Binomische Formel
- Kreis
- Standardabweichung
- Flächeninhalt
- Volumen Kugel
- Zahlen In Worten Schreiben
- Meter
- Orthogonalität
- Schriftlich Multiplizieren
- Brüche Multiplizieren
- Potenzgesetze
- Distributivgesetz
- Flächeninhalt Dreieck
- Rationale Zahlen
- Volumen Berechnen
- Brüche Addieren
- Kongruenz
- Exponentialfunktion
- Scheitelpunktform
- Logarithmus
- Erwartungswert
- Skalarprodukt
- Primfaktorzerlegung
- Quadratische Ergänzung
- Zinseszins
- Geradengleichung Aus Zwei Punkten Bestimmen
- Sinusfunktion


 Quadratische Funktionen f(x) = (x + d)²
Quadratische Funktionen f(x) = (x + d)²









