Thomson'sche Schwingungsgleichung – ungedämpfte elektromagnetische Schwingung

in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
Grundlagen zum Thema Thomson'sche Schwingungsgleichung – ungedämpfte elektromagnetische Schwingung
In diesem Video lernst du, wie die Differenzialgleichung einer ungedämpften elektromagnetischen Schwingung hergeleitet werden kann. Grundlage dafür ist der Vergleich der Energiebilanzen von Schwingkreis und Pendel. Vorab werden knapp die Vorgänge im Schwingkreis wiederholt. Zum Schluss des Videos werden die gelernten Inhalte zusammengefasst.
Transkript Thomson'sche Schwingungsgleichung – ungedämpfte elektromagnetische Schwingung
Die Thomson'sche Schwingungsgleichung: Ungedämpfte elektromagnetische Schwingung
Hallo, wir wollen uns heute mit der Herleitung der Thomsonschen Schwingungsgleichung für ungedämpfte elektromagnetische Schwingungen beschäftigen. Dazu wiederholen wir zunächst den elektrischen Schwingkreis bevor wir uns der mathematischen Beschreibung von Schwingkreis und Pendel zuwenden. Anschließend werden wir die Differenzialgleichung des Schwingkreises aufstellen was uns als Lösung zur Thomson‘schen Schwingungsgleichung führt.
Um das Video zu verstehen, solltest du folgende Sachverhalte bereits kennen: - die Energie in elektrischen und magnetischen Feldern - die Eigenschaften von Kondensatoren und Spulen - die Energiebilanz beim Federpendel sowie - die Eigenschaften und die Beschreibung harmonischer Schwingungen.
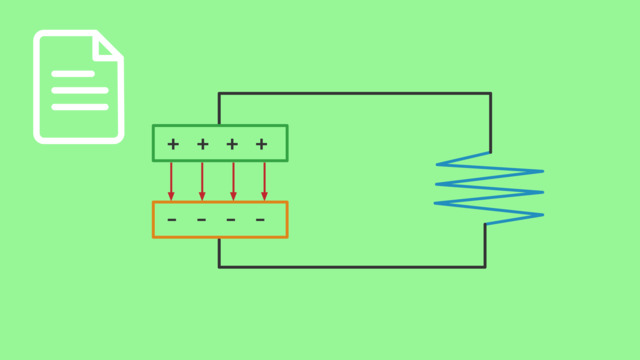
Wiederholen wir also zunächst den Schwingkreis. Wie du in diesem Schaltplan siehst, besteht er aus einem Kondensator und einer Spule in Reihenschaltung. Der bereits geladene Kondensator hat die elektrische Feldenergie E_elektrisch gleich Einhalb mal C mal U max Quadrat gespeichert. Wenn wir den Anteil des ohmschen Widerstands vernachlässigen, dann wird die elektrische Feldenergie vollständig in magnetische Feldenergie E_magnetisch gleich Einhalb mal der Induktivität L der Spule mal I max zum Quadrat umgewandelt.
Danach wird die magnetische Feldenergie wieder abgebaut und vollständig in elektrische Feldenergie des Kondensators umgewandelt. Dieser Vorgang wiederholt sich ständig und führt harmonische Schwingungen aus, daher der Name Schwingkreis. Dabei bleibt die Gesamtenergie konstant.
Wie können wir diesen Vorgang nun mathematisch beschreiben? Für die mathematische Beschreibung betrachten wir zunächst die Gesamtenergie des Schwingkreises: E_gesamt ist gleich E_magnetisch von t plus E_elektrisch von t ist gleich konstant.
Setzen wir die bekannten Größen ein, so erhalten wir: E_gesamt ist gleich Einhalb mal L mal I_Quadrat von t plus Einhalb mal C mal U_Quadrat von t gleich konstant.
Stromstärke und Spannung können wir auch als einen Ausdruck der Ladung schreiben. Dabei ist I von t ist gleich dQ nach dt, also Q_Punkt von t. Die Spannung U von t ist gleich C mal Q von t. Damit folgt: einhalb L mal Q_Punkt zum Quadrat von t plus Eins geteilt durch 2 C mal Q zum Quadrat von t ist gleich konstant. Da dieser Ausdruck konstant ist, ist seine Ableitung nach der Zeit gleich Null.
Leiten wir also nach der Zeit ab: L mal Q_Punkt von t mal Q_zwei_Punkt von t plus Eins geteilt durch C mal Q von t mal Q_Punkt von t ist gleich Null. Das Q_Punkt von t erscheint in beiden Summanden und wir können es ausklammern: Q_Punkt von t mal in Klammern L mal Q_zwei_Punkt von t plus Eins geteilt durch C mal Q von t ist gleich Null.
Wir wissen, dass ein Produkt genau dann Null ist, wenn einer der Faktoren gleich Null ist. Q_Punkt von t ist die Stromstärke I und die ist ja nicht ständig null. Also muss der Klammerinhalt gleich Null sein.
Dieser Klammerausdruck ist die Differenzialgleichung des ungedämpften Schwingkreises: L mal Q_zwei_Punkt von t plus Eins durch C mal Q von t ist gleich null. Nach Q_zwei_Punkt umgestellt, lautet die Gleichung dann: Q_zwei_Punkt von t gleich Minus Eins geteilt durch L und C mal Q von t.
Zur Lösung der Differenzialgleichung nutzen wir nun eine Analogiebetrachtung. Wir vergleichen die Schwingung eines Federpendels mit dem Schwingkreis. Die Differenzialgleichung des Pendels ist uns schon bekannt. Die Gleichung für das Pendel lautet: s_zwei_Punkt von t gleich Minus k geteilt durch m mal s von t.
Die Lösung der Pendelgleichung lautet: s gleich s_max mal sin in Klammern Omega mal t plus phi_null. Dabei ist Omega_Quadrat gleich k geteilt durch m und Omega somit gleich der Wurzel k geteilt durch m. Vergleichen wir den elektrischen Schwingkreis und das Pendel können wir nun folgende Analogien herstellen: die Ladung Q entspricht der Pendelauslenkung s, die Induktivität L der Spule entspricht der Kugelmasse m und der Kehrwert der Kapazität der Federkonstanten k.
Setzen wir die analogen Größen in die Lösung der Pendelgleichung ein, dann erhalten wir folgendes: Q ist gleich Q_max mal Sinus in Klammern Omega mal t plus Phi_Null. Weiter erhalten wir Omega_Quadrat gleich 1 geteilt durch L mal C und daraus schließlich Omega gleich 1 geteilt durch Wurzel L mal C.
Kommen wir nun zur Thomsonschen Schwingungsgleichung: Aus der Herleitung von eben haben wir bereits einen Ausdruck für die Kreisfrequenz Omega. Mit der allgemeinen Gleichung für die Kreisfrequenz Omega gleich zwei Pi mal f folgt dann für die Frequenz des Schwingkreises folgender Ausdruck: f gleich 1 geteilt durch 2 mal pi mal Wurzel aus L mal C.
Der Kehrwert der Frequenz ist die Schwingungsdauer T. Und somit ist T ist gleich 2 mal pi mal Wurzel aus L mal C. Dieser Ausdruck wird die Thomsonsche Schwingungsgleichung für den ungedämpften Schwingkreis genannt. Die Frequenz f wird dabei als Eigenfrequenz des Schwingkreises bezeichnet. Interessant ist, dass diese Eigenfrequenz nur von der Kapazität des Kondensators und der Induktivität der Spule abhängt.
Allerdings gilt diese Schwingungsgleichung nur für den idealisierten Fall, dass die ohmschen Widerstände im Schwingkreis vernachlässigt werden. Bei realen Schwingkreisen muss man das dann noch berücksichtigen.
Fassen wir das eben Gelernte mal zusammen: Die ungedämpfte elektromagnetische Schwingung in einem Schwingkreis stellt eine harmonische Schwingung dar. Die Thomsonsche Schwingungsgleichung für die ungedämpfte Schwingung in einem Schwingkreis lautet für die Eigenfrequenz f gleich 1 geteilt durch 2 mal pi mal Wurzel aus L mal C und anders geschrieben für die Schwingungsdauer T gleich 2 mal pi mal Wurzel aus L mal C.
Das war’s für heute – ich hoffe, Dir hat es etwas Spaß gemacht und Du hast alles verstanden – bis zum nächsten Mal!
Thomson'sche Schwingungsgleichung – ungedämpfte elektromagnetische Schwingung Übung
-
Beschreibe den Aufbau und die Wirkungsweise des Schwingkreises.
TippsErkennst du die Schaltzeichen in der Schaltung?
Wie funktioniert der Kondensator und was für ein Feld entsteht?
Wie funktioniert die Spule und was für ein Feld entsteht?
LösungWenn wir uns die Skizze anschauen, sehen wir, dass der Schwingkreis aus einem Kondensator und einer Spule besteht. Dies können wir auch seinem vollständigen Namen entnehmen: elektromagnetischer Schwingkreis. Elektromagnetisch steht hierbei für die Verbindung eines elektronischen und eines magnetischen Bauteils.
Gleichzeitig spiegelt der Name auch wider, welche Energien ineinander umgewandelt werden. Die elektrische Energie des Kondensators wird in magnetische Energie der Spule umgewandelt.
Zudem wird auch deutlich, welche Felder entstehen. Ein elektrisches Feld beim Kondensator und ein magnetisches bei der Spule.
Die Elektronen bewegen sich dabei wie bei einem normalen Schaltkreis durch den Leiter. Bei jedem Vorgang ändert sich dabei die Polarisation der Kondensatorplatten und auch die Orientierung der Felder.
-
Ordne die Begriffe richtig dem Schwingkreis, dem Fadenpendel oder beiden zu.
TippsDie Energieformen des Schwingkreises lassen sich aus dem vollständigen Namen des Schwingkreises ablesen: elektromagnetischer Schwingkreis.
Die Größen, die es sowohl im Schwingkreis als auch beim Fadenpendel gibt, beschreiben die Schwingung im Allgemeinen und nicht die konkreten Eigenschaften des Fadenpendels oder des Schwingkreises.
LösungEs gibt die Größen, die allgemein eine Schwingung beschreiben. Dies sind die Größen Periodendauer $T$ in Sekunden, Amplitude $A$ in Metern und Frequenz $f$ mit der Einheit Hertz als Kehrwert der Periodendauer $T$. Diese Größen werden also für die Beschreibung beider Versuche benötigt.
Beim Fadenpendel wird die Masse $m$ mit der Einheit Kilogramm um die Auslenkung $s$ mit der Einheit Meter aus der Ausgangslage verschoben. Dabei baut sich die potentielle Energie $E_{Pot}$ auf, welche beim Durchgang durch die Ruhelage komplett in kinetische Energie $E_{Kin}$ umgewandelt ist. Beide Energien haben die Einheit Joule.
Beim Schwingkreis wird der Kondensator mit einer Ladung Q aufgeladen. Dabei ist die elektrische Energie $E_{el}$ mit der Einheit Wattsekunde maximal. Der Kondensator hat dabei die Kapazität $C$ in Farad. Wenn sich der Kondensator entlädt, wird in der Spule mit der Induktivität L (Einheit Henry) ein magnetisches Feld aufgebaut. Dabei vergrößert sich die magnetische Feldstärke $B$.
-
Berechne die Periodendauer der Schwingung des Schwingkreises.
TippsDie Periodendauer T hat die Einheit s und ist der Kehrwert der Frequenz.
Die Frequenz hat die Einheit Hertz das ist $\frac{1}{s}$.
Das $\pi$ in der Formel bedeutet, dass eine Kreisfrequenz vorliegt.
LösungWir schauen uns an, was gegeben ist und was gesucht wird. Wir können daran erkennen, dass die Formel $T = 2 \pi \cdot \sqrt{C \cdot L}$ verwendet werden muss. Genau die gesuchten und gegebenen Größen sind in der Formel enthalten, jedoch keine andere.
In die Thomsonsche Schwingungsgleichung setzen wir dann die Werte für die Induktion und die Kapazität ein. Wir erhalten dann: $T = 2 \pi \cdot \sqrt{3 \cdot 3}=2 \pi \cdot \sqrt{9}=2 \pi \cdot 3=6 \pi$.
Der Stromkreis benötigt somit für eine komplette Schwingung 6$\pi$ Sekunden.
-
Erkläre was passieren würde, wenn kein idealer Schwingkreis vorliegt.
TippsVergleiche den Schwingkreis mit dem Fadenpendel.
Amplitude ist ein anderes Wort für die Auslenkung bei einem Fadenpendel.
Was würde es bedeuten, wenn sich die Frequenz oder die Periodendauer einer Schwingung ändern würde?
LösungUm die Frage zu beantworten, müssen wir uns zunächst die Eigenschaften der Schwingung anschauen. Sie besitzt besitzt eine Amplitude s und eine Frequenz f bzw. Periodendauer T.
Nun vergleichen wir den Schwingkreis mit dem Fadenpendel. Das Fadenpendel stoßen wir an und lassen es auspendeln. Dabei stellen wir fest, dass die Pendelschwingungen immer noch die gleiche Dauer besitzen, das Pendel aber nicht mehr so weit ausschlägt. Also wird durch die Reibung nur die Amplitude verkleinert, die Periodendauer und die Frequenz bleiben aber gleich groß.
-
Nenne die Thomsonsche Schwingungsgleichung
TippsDie Schwingungsgleichung beschreibt den elektromagnetischen Schwingkreis mathematisch.
Im elektromagnetischen Schwingkreis baut sich im Wechsel ein magnetisches Feld beziehungsweise elektrisches Feld auf.
Die Schwingung wird über die Eigenfrequenz oder ihren Kehrwert, die Periodendauer, beschrieben.
LösungZunächst überlegen wir uns, wovon eine elektromagnetische Schwingung abhängt.
Wir wissen, dass eine Schwingung sowohl eine Amplitude als auch eine Frequenz aufweist. Und wir erinnern uns daran, dass die Frequenz f der Kehrwert der Periodendauer T ist. Durch die Sinus-Wellenform der Schwingung wird deutlich, dass die Frequenz von der Kreisfrequenz $\omega$ bestimmt wird. $\omega = 2\pi f$
Die Abhängigkeiten im Schwingkreis werden über diese Gleichung beschrieben:
$\omega = \frac{1}{\sqrt{L \cdot C}}$
Wenn wir in diese Gleichung $\omega = 2\pi f$ einsetzen und nach f umstellen, erhalten wir die gewünschte Gleichung für die Frequenz f. Bilden wir von dieser den Kehrwert, erhalten wir die Gleichung für die Periodendauer T.
$f = \frac{1}{2 \pi \cdot \sqrt{L \cdot C}}$
$T = \frac{1}{f} = 2 \pi \cdot \sqrt{L \cdot C}$
-
Erkläre den Versuch zur Eignung eines Fadenpendels als Messgerät.
TippsDas Pendel wird wie jeder statische geladenen Körper von elektrischen Ladungen angezogen oder abgestoßen.
Die Kugel wird immer zur selben Ladung hin ausgelenkt.
Eine Periode ist immer die komplette Bewegung bis zum Anfangszustand.
LösungWir erinnern uns, dass ein geladener Körper sich in einem elektrischen Feld zu der entgegengesetzten Ladung bewegt. Weiterhin wissen wir, dass sich in einem Plattenkondensator ein homogenes elektrisches Feld aufbaut. Danach muss sich die positiv geladene Pendelkugel zu der Platte mit der negativen Ladung bewegen.
Wir wissen zudem, dass sich im Schwingkreis der Kondensator auflädt und sich wieder entlädt. Zudem baut sich in der Spule ein magnetisches Feld auf und wieder ab. Wenn der Kondensator wieder aufgeladen wird, ist die Ladung vertauscht, da die Elektronen von der einen Kondensatorplatte durch die Spule zur anderen Kondensatorplatte geflossen sind. Demnach muss das Pendel zwischen den Platten hin und her schwingen. Und da seine Bewegung durch das elektrische Feld angeregt wird, bewegt es sich mit derselben Frequenz wie die Elektronen im Schwingkreis. Das bedeutet, die Periodendauer des Strom ist genauso groß wie die Periodendauer des Pendels.
7.701
sofaheld-Level
6.601
vorgefertigte
Vokabeln
7.918
Lernvideos
37.080
Übungen
34.318
Arbeitsblätter
24h
Hilfe von Lehrer*
innen

Inhalte für alle Fächer und Klassenstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Physik
- Temperatur
- Schallgeschwindigkeit
- Dichte
- Transistor
- Drehmoment
- Lichtgeschwindigkeit
- Galileo Galilei
- Rollen- Und Flaschenzüge Physik
- Radioaktivität
- Lorentzkraft
- Beschleunigung
- Gravitation
- Hookesches Gesetz Und Federkraft
- Elektrische Stromstärke
- Elektrischer Strom Wirkung
- Reihenschaltung
- Ohm'Sches Gesetz
- Freier Fall
- Kernkraftwerk
- Atom
- Aggregatzustände
- Infrarot, Uv-Strahlung, Infrarot Uv Unterschied
- Isotope, Nuklide, Kernkräfte
- Transformator
- Trigonometrische Funktionen
- Lichtjahr
- Si-Einheiten
- Fata Morgana
- Gammastrahlung, Alphastrahlung, Betastrahlung
- Kohärenz Physik
- Mechanische Arbeit
- Schall
- Elektrische Leistung
- Dichte Luft
- Ottomotor Aufbau
- Kernfusion
- Trägheitsmoment
- Heliozentrisches Weltbild
- Energieerhaltungssatz Fadenpendel
- Linsen Physik
- Ortsfaktor
- Interferenz
- Diode
- Wärmeströmung (Konvektion)
- Schwarzes Loch
- Frequenz Wellenlänge
- Elektrische Energie
- Parallelschaltung
- Dopplereffekt, Akustischer Dopplereffekt
- Kernspaltung


 Du möchtest schneller & einfacher lernen?
Du möchtest schneller & einfacher lernen?

 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen











Hierbei ist es sinnvoll dir die Kettenregel anzuschauen
Danke, super strukturiert. Kann nur die Ableitung nach der Zeit nicht nachvollziehen, was aber eher an meinem mathematischen Unwissen liegen wird.