Sterne – Entstehung und Entwicklung

Inhaltsverzeichnis zum Thema

• Zustandsgrößen eines Sterns
• Entfernungsbestimmung eines Sterns
• Die Geburt eines Sterns
• Das Hertzsprung-Russell-Diagramm und der Lebenszyklus eines Sterns
  • Die Hauptreihensterne und der Beginn des Lebenszyklus eines Sterns
  • Riesen und Überriesen und das Heliumbrennen
  • Weiße Zwerge und das Endstadium eines Sterns
  • Hyperriesen – Wie groß können Sterne werden?

Zustandsgrößen eines Sterns

Die wichtigsten Zustandsgrößen eines Sterns sind seine Masse, Radius, Dichte, Oberflächentemperatur und absolute Helligkeit. Die Kenntnis dieser Größen erlaubt es Physikern, Vorhersagen zu treffen über das Alter und das Lebensende eines Sterns sowie seine Entfernung zu bestimmen. Doch wie ermittelt man die Zustandsgrößen eines Milliarden Kilometer weit entfernten Sterns?

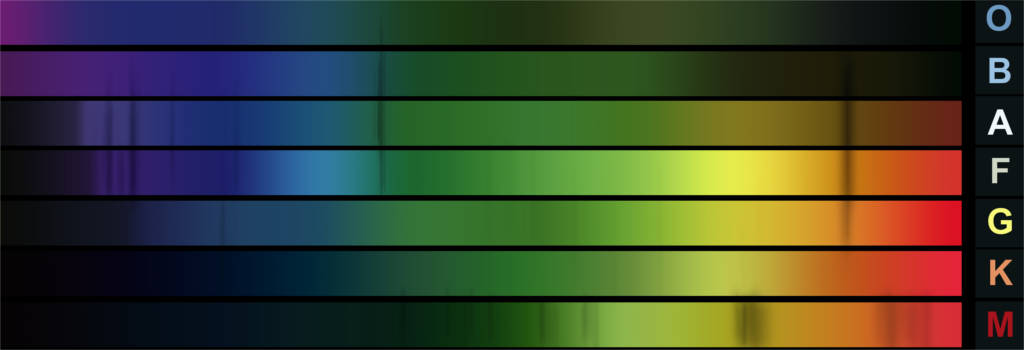
Das Absorptionsspektrum des Sterns (Spektralklasse) lässt sich auf der Erde mit entsprechenden Geräten bestimmen. Das Spektrum definiert seine Temperatur und die Rotverschiebung des Spektrums seine Entfernung. Außerdem liefert das Spektrum eines Sterns Indizien für dessen Masse und Radius. Finden Physiker Doppelsternsysteme, das sind zwei Sterne, die sich umkreisen, können sie aus der Umlaufzeit unter Anwendung der Keplerschen Gesetze ebenfalls die Masse bestimmen.

Entfernungsbestimmung eines Sterns

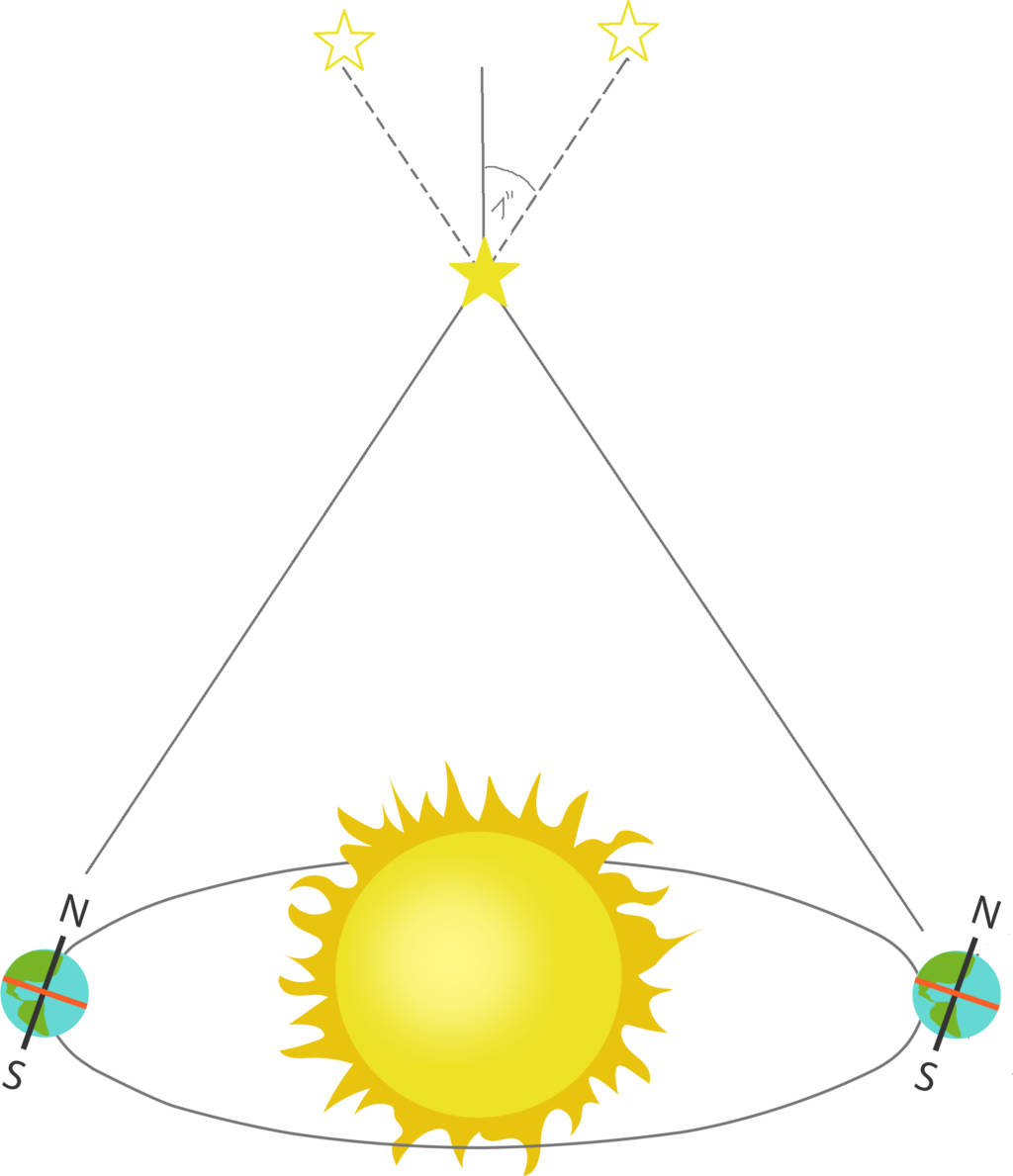
Die Helligkeit eines Sterns nimmt ab, je weiter er von der Erde entfernt ist. Demnach können Physiker auch aus der scheinbaren Helligkeit des Sterns seinen Abstand ermitteln. Eine weitere Methode zur Entfernungsbestimmung eines Sterns ist die Parallaxen-Methode. Dabei notieren sich die Wissenschaftler die scheinbare Position eines Sterns am Himmel. Ein halbes Jahr später, wenn die Erde auf der gegenüberliegen Seite der Sonne steht, bestimmen sie erneut die Position des Sterns am Himmel. Da der Beobachtungspunkt (die Erde) sich verändert hat, erscheint auch die Position des Sterns verschoben. Anhand der Verschiebung lässt sich auf die Entfernung schließen. Hat sich die scheinbare Position des Sterns um eine Bogensekunde verändert, so ist er ein Parsec (von Parallaxensekunde) entfernt. Ein Parsec entspricht $3,086\cdot10^{13}\,$km bzw. $3,26\,$ Lichtjahren. Ein Lichtjahr ist der Weg, den Licht in einem Jahr zurücklegt.

Die Geburt eines Sterns

Viele Millionen Jahre nach dem Urknall bestand das Universum nur aus Staub und Nebeln aus Wasserstoff und Helium. Aufgrund ihrer eigenen Gravitation bilden sich aus den Staubpartikeln große Wolken, die immer mehr Masse in sich vereinigen. Je mehr Wasserstoff aus der Umgebung gesammelt wird, desto größer wird die Gravitation. Die interstellare Wolke kollabiert schließlich und bildet einen Protostern. Das ist der Beginn eines jeden Sternlebens. Mit stetiger Massenzunahme erhöht sich der Druck und die Temperatur im Inneren des Protosterns, bis eine Kernfusion gezündet wird. Von nun an verbrennt Wasserstoff zu Helium. Der Protostern ist zu einem Stern geworden, der eine stabile Größe hat und leuchtet. Jetzt befindet er sich auf der Hauptreihe des Hertzsprung-Russell-Diagramms.

Das Hertzsprung-Russell-Diagramm und der Lebenszyklus eines Sterns

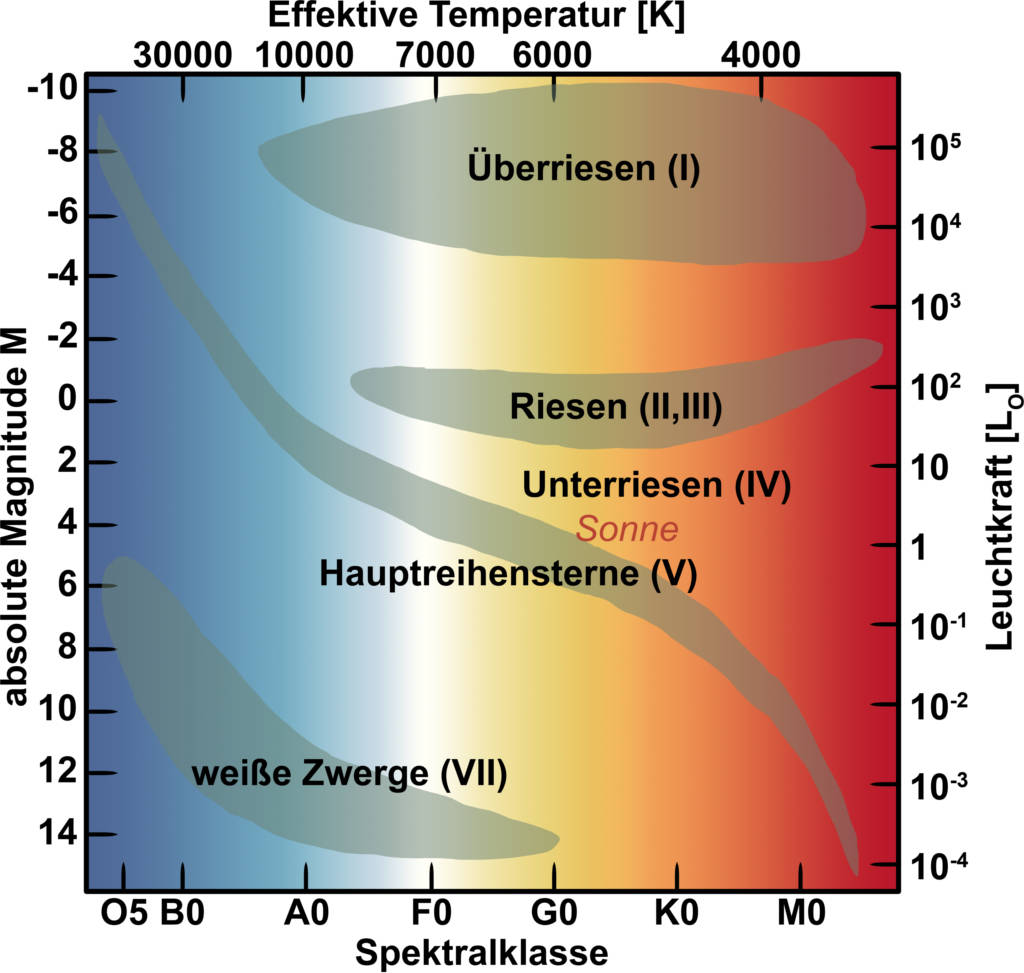
Das Hertzsprung-Russell-Diagramm (HRD) visualisiert den Zusammenhang zwischen der Farbe eines Sterns (Spektralklasse) und dessen Helligkeit (Leuchtkraft). Es wurde eingeführt, um die vielen entdeckten Sterne zu kategorisieren und zu ordnen. Im Prinzip stellt jeder Bereich des Diagramms einen Zeitpunkt im Leben eines Sterns dar und da alle Sterne unterschiedlich alt sind, können Physiker in jedem Bereich Sterne entdecken, je nach Fortschritt ihres Lebenszyklus. Könnten Astronomen einen einzelnen Stern über Jahrmillionen beobachten, so würde der Stern im Diagramm "wandern".

Die Hauptreihensterne und der Beginn des Lebenszyklus eines Sterns

Die Hauptreihensterne, die auf der Diagonale des Diagramms liegen, befinden sich im ersten Stadium ihres Lebenszyklus, das gleichzeitig das längste ist. Unten rechts findest du Sterne, die mit $0,3$ Sonnenmassen leichter sind als die Sonne. Da sie weniger Brennstoff zur Verfügung haben, werden sie nur $2000\,$K heiß und leuchten daher rot. Am oberen linken Ende findest du Sterne, die mit $60$ Sonnenmassen viel schwerer als die Sonne sind, $50000\,$K heiß werden und daher blau leuchten. Die Hauptreihensterne werden als Zwerge bezeichnet. Die blauen Zwerge leben sehr viel kürzer als die roten Zwerge, da sie ihr zur Verfügung stehendes Brennmaterial schneller verbrennen.

Riesen und Überriesen und das Heliumbrennen

In einem Stern herrscht ein ständiges Wechselspiel zwischen der Eigengravitation, die versucht, den Stern zu komprimieren, und dem Druck der emittierten Strahlung, die den Stern aufzublähen versucht. Ist der Großteil des Wasserstoffs eines Sterns zu Helium verbrannt, beginnt in der Regel das Heliumbrennen, bei dem Helium zu Kohlenstoff verbrannt wird. Da nun der Strahlungsdruck im Stern überwiegt, beginnt er sich aufzublähen und auf ein Vielfaches seiner ursprünglichen Größe anzuwachsen: Aus roten Zwergen werden rote Riesen. Da blaue Zwerge mehr Masse haben, wird das Helium sogar noch weiter zu schwereren Elementen verbrannt (Schalenbrennen) und so werden aus blauen Zwergen Überriesen. Riesen leuchten heller als Hauptreihensterne und rot, da die Oberflächentemperatur mit zunehmender Größe sinkt. Im Hertzsprung-Russell-Diagramm sind die Riesen oberhalb der Hauptreihe zu finden.

Weiße Zwerge und das Endstadium eines Sterns

Das Ende eines Sterns hängt sehr stark von seiner Masse ab. Diese wird häufig mit dem Vielfachen der Sonnenmasse angegeben.

• Hat der rote Riese zu Beginn seines Lebenszyklus eine Masse, die kleiner ist als die $1,44$-fache Sonnenmasse und hat er seinen Brennstoff vollständig verbraucht, so stößt er die äußere leichte Hülle ins All ab und zurück bleibt ein weißer Zwerg mit der Masse eines Sterns aber nur noch der Größe eines Planeten. Ein weißer Zwerg ist so etwas wie der harte Kern eines Riesen, der sehr heiß ist (daher weiß), aber nur noch schwach leuchtet, da der Brennvorgang erloschen ist. Du findest weiße Zwerge im HRD daher unterhalb der Hauptreihe. Die wird auch das Ende unserer Sonne sein.

• Hat ein Riese (meist Überriese) zu Beginn eine Masse, die größer ist als das $1,44$-fache der Sonnenmasse, so explodiert er am Ende seines Lebens aufgrund komplizierter physikalischer Vorgänge in einer Supernova. Die Hülle des Sterns wird dabei explosionsartig ins All gestoßen und zurück bleibt ein Neutronenstern, der nur wenige Kilometer Durchmesser hat. Da er trotzdem die Masse einer Sonne hat, gehört ein Neutronenstern zu den dichtesten Objekten im Universum.

• Noch dichter sind nur noch schwarze Löcher. Diese entstehen nach einer Supernova, wenn der ursprüngliche Stern mehr Masse als das $2,5 - 3$-fache der Sonnenmasse hatte. Dann ist der Neutronenstern so schwer, dass er kollabiert.

Da schwarze Löcher und Neutronensterne nicht leuchten, sind sie auch nicht auf dem Hertzsprung-Russell-Diagramm zu finden. Jedoch haben die schwarzen Löcher so eine große Masse, dass sie viele Sterne zu sich hinziehen. Daher ist es im Zentrum unserer Galaxie trotz des schwarzen Loches in seiner Mitte sehr hell.

Hyperriesen – Wie groß können Sterne werden?

Astronomen legten sich auf die rechnerische Obergrenze von ca. 150 Sonnenmassen für einen stabilen Stern fest. Doch heute kennen wir bereits schwerere Sterne, sogenannte Hyperriesen. 2010 konnte die Masse von R136a1 annähernd bestimmt werden, etwa 265 Sonnenmassen. Dabei ist sein Durchmesser auch 35 mal so groß wie der der Sonne. Von diesem Stern geht eine Leuchtkraft aus, 10-millionenmal heller als die Sonne. Im Vergleich hätte die Sonne die Leuchtkraft eines Glühwürmchens, dann hätte R136a1 die Leuchtkraft einer 100W Lampe. Dieser Stern ist zu schwer und leuchtstark auf unserem HRD verzeichnet zu sein. Man geht davon aus, dass dieser Stern durch die Fusion mehrerer Sterne entstanden ist. Daher bleibt die obere Massengrenze für die normale Entwicklung eines Sterns weiterhin gültig.