Impuls und Impulserhaltung
Impuls; Impulserhaltungssatz; Stöße; Raketengleichung
Beliebteste Videos
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Der Impuls als physikalische Größe
- Die Impulserhaltung
- elastische Stöße
- inelastische Stöße
- Impuls beim Raketenstart
Der Impuls als physikalische Größe
Der Impuls ist eine physikalische Größe, mit der sich Körper in Bewegung beschreiben lassen. Jeder Körper, der eine Masse besitzt und sich bewegt, besitzt einen Impuls $p$. Je mehr Masse der Körper besitzt und je schneller er sich bewegt, desto größer ist sein Impuls. So hat ein Containerschiff, welches sich mit voller Fahrt bewegt, einen größeren Impuls als eine Gewehrkugel, welche sich zwar viel schneller bewegt, jedoch eine viel kleinere Masse besitzt. Bei Impulsbetrachtungen werden häufig Kollisionen betrachtet, physikalisch Stöße genannt. Dabei beschreibt der Impuls die mögliche Kraftwirkung des Körpers auf einen anderen. Daher wird der Impuls auch häufig vereinfacht und umgangssprachlich als Wucht bezeichnet. Berechnen lässt sich der Impuls als Produkt aus Masse und Geschwindigkeit.
$p=m\cdot v~$mit$~[p]=1~\frac{\text{kg}\cdot\text{m}}{\text{s}}=1~\text{N}\cdot \text{s}$
Da die Geschwindigkeit $v$ eine gerichtete, also vektorielle Größe ist, ist auch der Impuls $p$ als mögliches Produkt der Multiplikation mit einer absoluten Zahl wie der Masse $m$ eine vektorielle und damit gerichtete Größe.
$\vec{p}=m\cdot \vec{v}$
Dies ist für die Stoßbetrachtungen von fundamentaler Bedeutung.
Die Impulserhaltung
Wie auch bei der bereits bekannten Energieerhaltung gilt auch für die Betrachtung von Impulsen ein Erhaltungssatz: der Impulserhaltungssatz. So gehen Impulse in einem idealen, also reibungsfreien System stets vollständig in die Wechselwirkung ein. Diese Wechselwirkung und das Ergebnis einer solchen Wechselwirkung lassen sich mit den zwei Stoßarten beschreiben.
Damit ist die Summe aller Impulse in einem solchen System konstant:
$\sum\limits_{k=1}^{n} \vec{p_k}=\text{konst.}$
elastische Stöße
Bei elastischen Stößen in einem idealen System wird der Impuls beim Stoß in Abhängigkeit von den Massen der beteiligten Körper neu verteilt. Dabei wird der komplette Impuls in die erneute Bewegung beider Körper umgesetzt, also keine Bewegungsenergie in innere Energie umgewandelt.
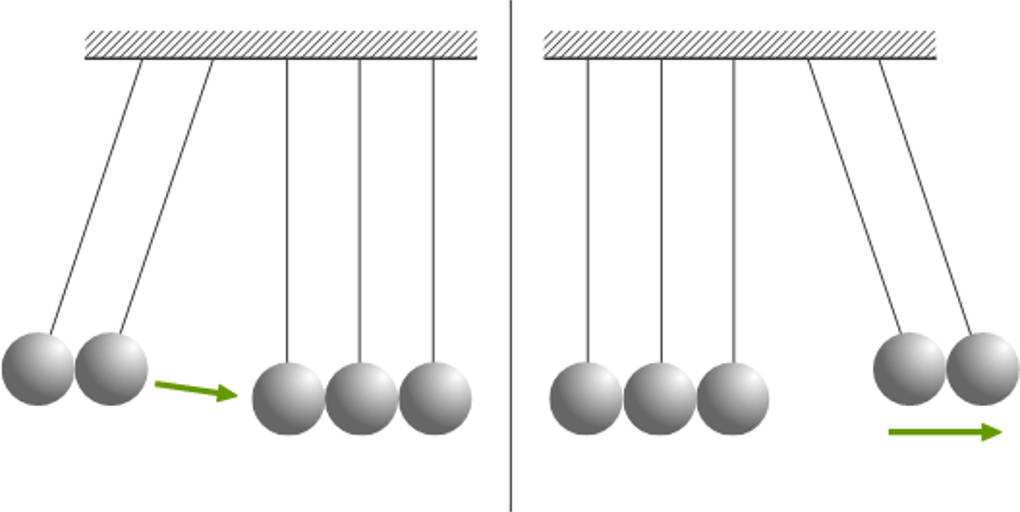
Ein sehr gutes Beispiel für diese Stoßart ist das Newtonpendel. Bei diesem hängen 5 Kugeln an jeweils 2 Fäden in einem Gestell. Lenkt man nun zwei Kugeln auf einer Seite aus und lässt diese mit den restlichen Kugeln kollidieren, werden die zwei Kugeln auf der anderen Seite des Pendels ausgelenkt während die vorher ausgelenkten Kugeln nun ruhig neben der mittleren Kugel ruhen. Der Impuls wurde komplett übertragen.
Gleichungen für den zentralen elastischen Stoß:
$m_1 \cdot \vec{v_1} + m_2 \cdot \vec{v_2} = m_1 \cdot \vec{u_1} + m_2 \cdot \vec{u_2}$
Dabei ist $\vec{v}$ die Geschwindigkeit vor dem Stoß und $\vec{u}$ die Geschwindigkeit nach dem Stoß. Diese lässt sich für die beiden einzelnen Körper wie folgt bestimmen:
$u_1=\frac{(m_1-m_2)v_1+2m_2 \cdot v_2}{m_1+m_2}$
und
$u_2=\frac{(m_2-m_1)v_2+2m_1 \cdot v_1}{m_1+m_2}$
Dabei gilt für die kinetische Energie:
$E_{kin, a} = E_{kin, e}; \Delta E_{kin}=0$
inelastische Stöße
Bei inelastischen Stößen können sich ein Körper oder beide Körper verformen. Auf diese Weise wird bei einem Stoß ein Teil der kinetischen Energie in innere Energie umgewandelt. Beim vollkommenen inelastischen Stoß verhaken sich beide Körper ineinander und setzen ihren Weg als ein Körper mit kombinierter Masse fort.
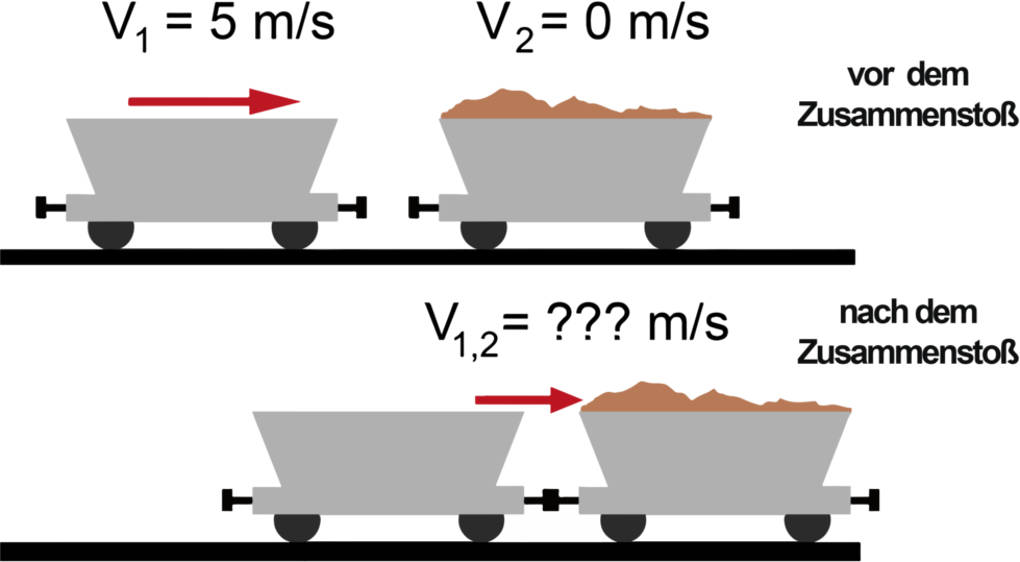
Ein gutes Beispiel dafür ist ein Güterwagen, der gegen einen anderen rollt und dabei ankoppelt. Die beiden rollen dann gemeinsam ein Stück weiter.
Gleichung für den inelastischen Stoß:
$m_1 \cdot \vec{v_1} + m_2 \cdot \vec{v_2} = (m_1 + m_2)\vec{u}$
Dabei ist $\vec{v}$ die Geschwindigkeit vor dem Stoß und $\vec{u}$ die Geschwindigkeit nach dem Stoß. Diese lässt sich für die beiden nun verhakten Körper wie folgt bestimmen:
$u=\frac{m_1\cdot v_1 + m_2 \cdot v_2}{m_1+m_2}$
Die energetische Betrachtung ist jedoch wegen der Zunahme der inneren Energien etwas komplexer:
$E_{kin, a} > E_{kin, e}$
$\Delta E_{kin} = \frac 12 (m_1 \cdot v_1^2+m_2 \cdot v_2^2)-\frac 12 u^2(m_1+m_2)=\frac{m_1 \cdot m_2}{2(m_1+m_2)}\cdot (v_1-v_2)^2$
Impuls beim Raketenstart
Beim Start einer Weltraummission ist die Erlangung des nötigen Impuls und dessen Erhaltung sehr wichtig. Zudem wird durch Abwurf von weiterer Masse wie der Trägerrakete der Geschwindigkeitsanteil des Impulses sehr stark erhöht. Damit erlangt man genug Geschwindigkeit, um die Anziehung der Erde zu überwinden.
Um die nötige Masse und Geschwindigkeit genau zu berechnen, verwendet man die Raketengleichung.
Alle Videos zum Thema
Videos zum Thema
Impuls und Impulserhaltung (7 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Impuls und Impulserhaltung (7 Arbeitsblätter)
Beliebteste Themen in Physik
- Temperatur
- Schallgeschwindigkeit
- Dichte
- Transistor
- Drehmoment
- Lichtgeschwindigkeit
- Galileo Galilei
- Rollen- Und Flaschenzüge Physik
- Radioaktivität
- Lorentzkraft
- Beschleunigung
- Gravitation
- Hookesches Gesetz Und Federkraft
- Elektrische Stromstärke
- Elektrischer Strom Wirkung
- Reihenschaltung
- Ohm'Sches Gesetz
- Freier Fall
- Kernkraftwerk
- Atom
- Aggregatzustände
- Infrarot, Uv-Strahlung, Infrarot Uv Unterschied
- Isotope, Nuklide, Kernkräfte
- Transformator
- Trigonometrische Funktionen
- Lichtjahr
- Si-Einheiten
- Fata Morgana
- Gammastrahlung, Alphastrahlung, Betastrahlung
- Kohärenz Physik
- Mechanische Arbeit
- Schall
- Elektrische Leistung
- Dichte Luft
- Ottomotor Aufbau
- Kernfusion
- Trägheitsmoment
- Heliozentrisches Weltbild
- Energieerhaltungssatz Fadenpendel
- Linsen Physik
- Ortsfaktor
- Interferenz
- Diode
- Wärmeströmung (Konvektion)
- Schwarzes Loch
- Frequenz Wellenlänge
- Elektrische Energie
- Parallelschaltung
- Dopplereffekt, Akustischer Dopplereffekt
- Kernspaltung










 Was ist der Impuls?
Was ist der Impuls?
 Inelastischer Stoß
Inelastischer Stoß
 Zentraler und nicht-zentraler elastischer Stoß
Zentraler und nicht-zentraler elastischer Stoß
 Impulserhaltungssatz
Impulserhaltungssatz
 Raketengleichung
Raketengleichung
 Drehimpuls
Drehimpuls
 Drehmoment
Drehmoment









