für alle Fächer und Klassenstufen
-
Mit Spaß & ohne Druck lernen
dank witziger Geschichten -
Nachhaltig & spielerisch
wiederholen mit mehreren Sinnen -
Inhalte von Lehrer*innen
erstellt & geprüft
Mehr zu Lernvideos
zur Festigung des Lernstoffs
-
Spielend Wissenslücken
aufdecken & schließen -
Entspannt & angstfrei
auf Klassenarbeiten & Tests vorbereiten -
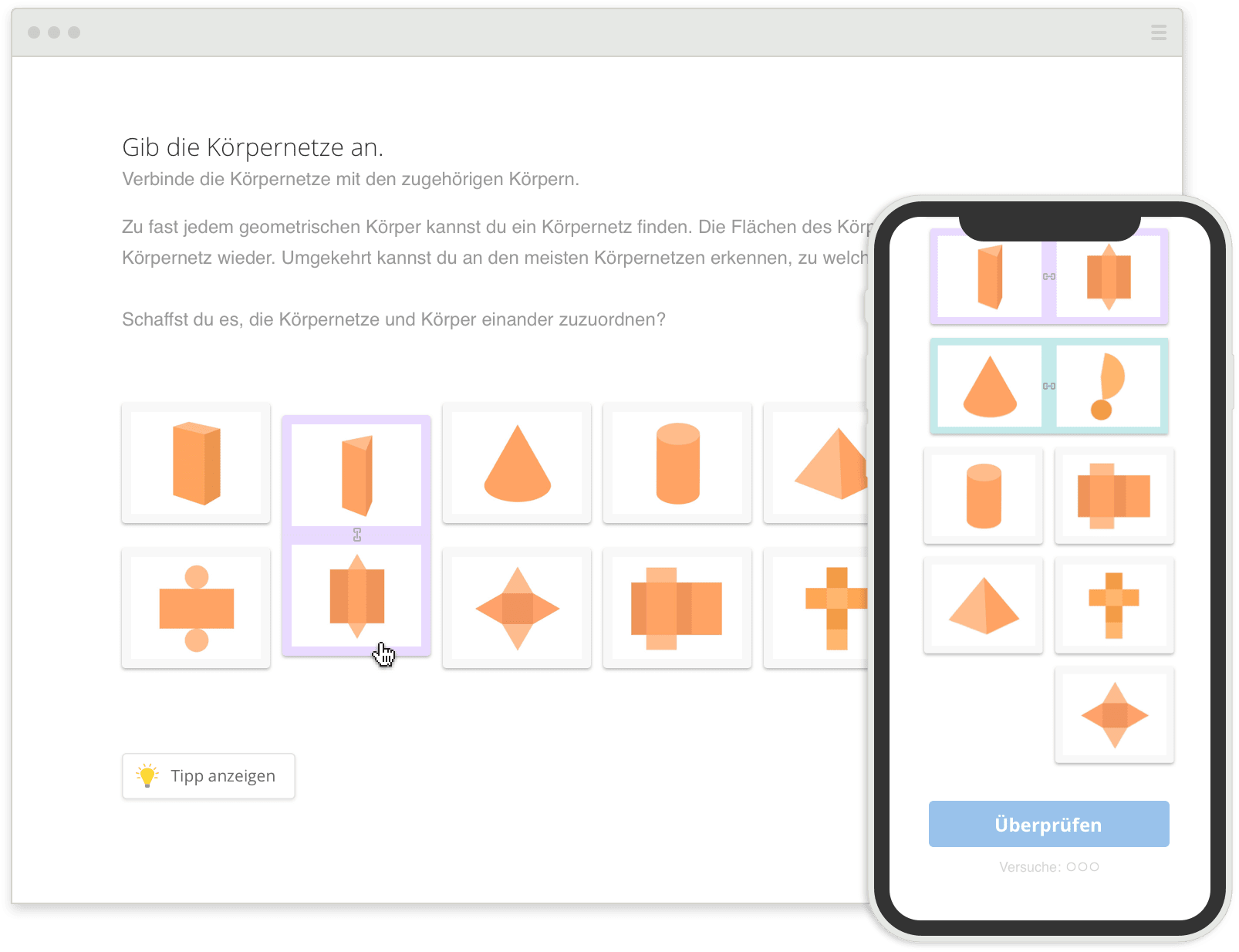
Lösungswege nachvollziehen &
Schritt für Schritt verstehen
Mehr zu den Übungen
für Englisch, Französisch & Spanisch
- Bequem Vokabeln üben – dank kinderleichter Anwendung
- Nachhaltig & vielfältig lernen – mit mehreren Sinnen
- Gezielt & motivierend abfragen lassen – passend zum Lernstand Mehr zum Vokabeltrainer
-
 Lernspiel Sofaheld
Lernspiel Sofaheldfür selbstständiges Üben
-
Spannende Lernabenteuer meistern & Erfolge feiern
-
Spielerisch den Schulstoff der 1. bis 7. Klasse verstehen
-
Selbstständig & motiviert üben – ohne die Hilfe Erwachsener
-
-
 Arbeitsblätter
Arbeitsblätterzum Lernen – auch ohne Bildschirm
-
Motiviert & abwechslungsreich üben dank vielfältiger Aufgaben
-
Gezielt & konzentriert wiederholen für Klassenarbeiten & Tests
-
Selbstständig Lösungen überprüfen & Erfolge feiern
-
-
 24h-Hilfe
24h-Hilfedank Hausaufgaben-Chat & Lehrerbox
-
Schnelle Antworten auf individuelle Fragen zum Schulstoff
-
Hilfe von Fachexpert/-innen Mathe, Deutsch, Englisch, Physik, Chemie, Biologie, Französisch, Latein
-
Entlastung der Eltern bei Schulthemen
-
Ich habe meine noten verbessert ❤️
Die Aufgaben sind total gut! Endlich verstehe ich das Thema
Coole Lernmethoden es wird alles gut beigebracht und gute Lernvideos
Ich finde schön, dass es den Kindern oder Schülern gut erklärt wird und verständnisvolle Aufgaben gegeben werden.
Die Kinder kommen schnell ins Lernsystem und arbeiten tatsächlich freiwillig auf der Plattform. Mehrere Kinder in verschiedenen Klassenstufen klappt super!
Beliebteste Themen
Mathematik
Deutsch
- Präteritum
- Perfekt
- Präsens
- Artikel
- Subjekt
- Plusquamperfekt
- Umlaute
- Bestimmte Und Unbestimmte Artikel
- Buchvorstellung Planen
- Pronomen Grundschule
- Selbstlaute, Doppellaute Und Umlaute Erkennen
- Was Ist Ein Subjekt
- Possessivpronomen
- Anapher
- Gedichtinterpretation Schluss
- Prädikat
- Konjunktiv I
- Denotation, Konnotation
- Wortarten
- Metapher
Englisch
- Simple Past
- Simple Present
- Present Perfect
- Present Progressive
- Writing An Essay
- Present Participle
- Past Perfect
- If-Clauses
- Past Participle
- Irregular Verbs Kategorien
- Bildbeschreibung Englisch
- American Dream
- Genitiv-S Englisch
- Going To-Future
- Mediation Englisch
- Will-Future
- Vergleich Deutsches Und Englisches Schulsystem
- Linking Words
- Past Perfect Progressive
- Englisch Zahlen 1 Bis 20
Biologie
Physik
- Temperatur
- Schallgeschwindigkeit
- Dichte
- Transistor
- Drehmoment
- Lichtgeschwindigkeit
- Galileo Galilei
- Rollen- Und Flaschenzüge Physik
- Radioaktivität
- Lorentzkraft
- Beschleunigung
- Gravitation
- Hookesches Gesetz Und Federkraft
- Elektrische Stromstärke
- Elektrischer Strom Wirkung
- Reihenschaltung
- Ohm'Sches Gesetz
- Freier Fall
- Kernkraftwerk
- Atom








































Mein Kind (9) hat sich von 4’ern nach zwei Monaten auf 2’er in Mathe und sogar eine eins in Deutsch und in Englisch hochgearbeitet. Ich kann es nur empfehlen! 😊👍 Bin totaler Befürworter!
Ich liebe euch 🙏😉 meine Maus geht jetzt in die 8. Klasse Gymnasium und arbeitet selbstständig (!!) mit euren Lern- und Übungsvideos. Erst wenn ihr nicht mehr helfen könnt muss ich ran 😅 tolle Plattform !!!
Ich habe es damals für meinen Sohn bezogen und es hat ihm so viel Spaß gemacht, dass er wirklich ein megaaa Zeugnis hatte. Kann es nur empfehlen!