Ebenengleichungen
In der analytischen Geometrie lernst du Ebenen kennen. Hier siehst du, wie du eine Ebenengleichung aufstellen kannst und welche Darstellungsformen es für Ebenen gibt.
Beliebteste Videos
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Die Parametergleichung einer Ebene
- Von der Parametergleichung zur Normalengleichung
- Von der Normalengleichung zur Koordinatengleichung
Die Parametergleichung einer Ebene
Ebenen sind entweder durch einen Punkt und zwei Vektoren oder durch drei Punkte gegeben. Dabei muss gelten:
- Die Vektoren sind nicht kollinear.
- Die drei Punkte liegen nicht auf einer Geraden.
Eine Parametergleichung sieht so aus:
$E:\vec x=\vec a+r\cdot \vec u+s\cdot \vec v$
Dabei ist
- $\vec x$ ein Vektor, der auf einen beliebigen Punkt der Ebene zeigt,
- $\vec a$ ein Vektor, der auf einen gegebenen Punkt der Ebene zeigt, der Stützvektor,
- $\vec u$ sowie $\vec v$ die Richtungsvektoren und
- $r\in\mathbb{R}$ sowie $s\in\mathbb{R}$ Parameter.
Wir beginnen mit der sogenannten Drei-Punkte-Gleichung, einer Ebenengleichung in Parameterform aus drei Punkten.
Gegeben sind die drei Punkte $A(1|2|1)$. $B(2|1|2)$ sowie $C(1|3|3)$. Zunächst bestimmst du die Verbindungsvektoren von jeweils zwei Punkten:
$\vec{AB}=\begin{pmatrix} 1\\-1\\1 \end{pmatrix}$
$\vec{AC}=\begin{pmatrix} 0\\1\\2 \end{pmatrix}$
Da die beiden Vektoren nicht kollinear sind, kannst du folgern, dass die drei Punkte eine Ebene aufspannen. Nun kannst du die Ebenengleichung in Parameterform aufschreiben. Du nimmst den Ortsvektor von einem der drei Punkte, hier $A$, als Stützvektor und die beiden Verbindungsvektoren als Richtungsvektoren:
$E:\vec x=\begin{pmatrix} 1\\2\\1 \end{pmatrix}+r\cdot \begin{pmatrix} 1\\-1\\1 \end{pmatrix}+s\cdot \begin{pmatrix} 0\\1\\2 \end{pmatrix}$
Hier siehst du eine Ebene, die durch drei Punkte gegeben ist.

Von der Parametergleichung zur Normalengleichung
Um die Ebenengleichung in Normalenform aufzustellen, benötigst du einen Normalenvektor $\vec n$. Dieser steht senkrecht zu der Ebene.
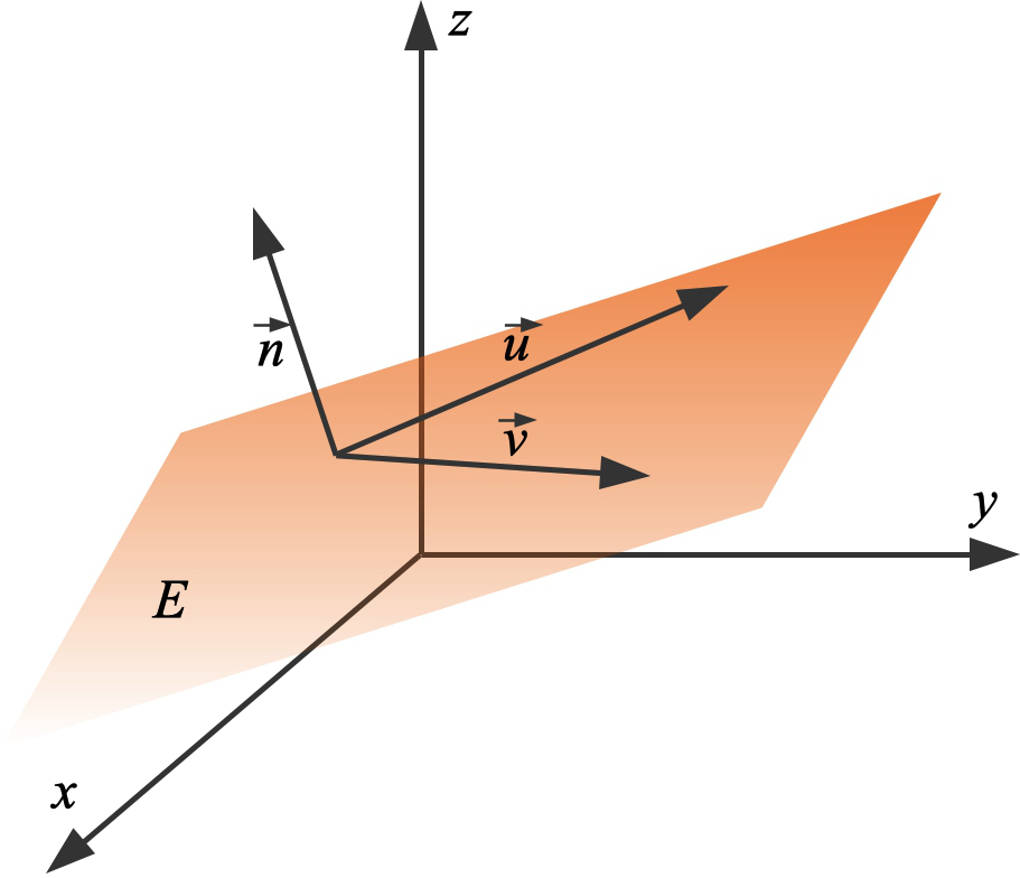
Bestimmen eines Normalenvektors
Den Normalenvektor erhältst du als Vektorprodukt der beiden Richtungsvektoren. In dem obigen Beispiel ist ein Normalenvektor wie folgt gegeben:
$\vec n=\begin{pmatrix} 1\\-1\\1 \end{pmatrix}\times \begin{pmatrix} 0\\1\\2 \end{pmatrix}=\begin{pmatrix} -3\\-2\\1 \end{pmatrix}$
Nun kannst du die Ebenengleichung in Normalenform aufschreiben:
$E:\left(\vec x-\begin{pmatrix} 1\\2\\1 \end{pmatrix}\right)\star\begin{pmatrix} -3\\-2\\1 \end{pmatrix}=0$
Dabei steht $\star$ für das Skalarprodukt zweier Vektoren.
Die Hessesche Normalenform
Eine besondere Normalenform ist die Hessesche Normalenform. Da in der Normalengleichung auf der rechten Seite die skalare $0$ steht, kannst du die Gleichung mit einem Faktor multiplizieren, ohne dadurch die Ebene zu verändern. Multiplizierst du die Normalengleichung mit dem Kehrwert der Länge des Normalenvektors, erhältst du:
$E:\frac{1}{\sqrt{14}}\left(\vec x-\begin{pmatrix} 1\\2\\1 \end{pmatrix}\right)\star\begin{pmatrix} -3\\-2\\1 \end{pmatrix}=0$
Dies ist die Hessesche Normalenform. Du benötigst diese zur Abstandsberechnung.
Von der Normalengleichung zur Koordinatengleichung
Zu guter Letzt lernst du noch die Ebenengleichung in Koordinatenform kennen. Von der Normalengleichung ausgehend kannst du die Koordinatengleichung aufschreiben:
$E: -3x-2y+z=-6$
Dabei sind die Faktoren $-3$, $-2$ und $1$ vor den Koordinaten $x$, $y$ und $z$ gerade die Koordinaten des Normalenvektors. Auf der rechten Seite der Koordinatengleichung steht das Skalarprodukt $\vec a\star \vec n$ mit dem Stützvektor $\vec a$ sowie dem Normalenvektor $\vec n$.
Dividierst du nun die Koordinatengleichung durch die rechte Seite, so erhältst du:
$E: \frac12 x+\frac13y-\frac16 z=1$
Dies ist die Achsenabschnittsform der Ebene. Der Name rührt daher, dass du damit die Achsenabschnitte, die Schnittstellen der Ebene mit den Koordinatenachsen, bestimmen kannst. Diese sind jeweils gegeben durch die Kehrwerte der Faktoren vor den Koordinaten.
Zum Beispiel schneidet die Ebene bei $x=2$ die $x$-Achse, bei $y=3$ die $y$-Achse und bei $z=-6$ die $z$-Achse.
Alle Videos zum Thema
Videos zum Thema
Ebenengleichungen (5 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Ebenengleichungen (5 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Primzahlen
- Geometrische Lagebeziehungen
- Rechteck
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Quadrat
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Was Ist Eine Viertelstunde
- Prisma
- Mitternachtsformel
- Grundrechenarten Begriffe
- Dreiecksarten
- Quader
- Satz Des Pythagoras
- Dreieck Grundschule
- Erste Binomische Formel
- Kreis
- Standardabweichung
- Flächeninhalt
- Volumen Kugel
- Zahlen In Worten Schreiben
- Meter
- Orthogonalität
- Schriftlich Multiplizieren
- Brüche Multiplizieren
- Potenzgesetze
- Distributivgesetz
- Flächeninhalt Dreieck
- Rationale Zahlen
- Volumen Berechnen
- Brüche Addieren
- Kongruenz
- Exponentialfunktion
- Scheitelpunktform
- Logarithmus
- Erwartungswert
- Skalarprodukt
- Primfaktorzerlegung
- Quadratische Ergänzung
- Zinseszins
- Geradengleichung Aus Zwei Punkten Bestimmen
- Sinusfunktion









 Parameterform einer Ebene
Parameterform einer Ebene
 Normalenform einer Ebene
Normalenform einer Ebene
 Koordinatenform einer Ebene
Koordinatenform einer Ebene
 Von der Koordinatenform in die Parameterform
Von der Koordinatenform in die Parameterform
 Ebenengleichungen mit Parametern – Ebenenscharen
Ebenengleichungen mit Parametern – Ebenenscharen









