Volumen und Oberfläche von Kegeln

Inhaltsverzeichnis zum Thema

• Was ist ein Kegel?
  • Die Flächen eines Kegels
  • Beispiele für Kegel
• Verschiedene Kegel
  • Gerade Kegel
  • Schräge Kegel
• Die Mantel- und Oberfläche eines Kegels
  • Die Grundfläche
  • Die Mantelfläche
  • Die Oberfläche
• Das Volumen eines Kegels
• Beispiel – Paul bastelt eine Schultüte
• Beispiel – Wie viel Saft passt in ein kegelförmiges Glas?
• Der Kegelstumpf
  • Die Mantel- und Oberfläche eines Kegelstumpfes
  • Das Volumen eines Kegelstumpfes
  • Beispiel

Was ist ein Kegel?

Ein Kegel ist ein geometrischer Körper.

• Die Grundfläche eines Kegels ist ein Kreis.
• Jeder Punkt des Kreisrandes wird mit der Spitze des Kegels verbunden.

Ein Kegel hat somit

• eine Ecke, dies ist die Spitze,
• eine Kante, den Rand des Kreises als Grundfläche, sowie
• zwei Flächen.

Die Flächen eines Kegels

Ein Kegel besteht aus

• einem Kreis als Grundfläche sowie
• einem Kreisausschnitt als Mantel.

Beispiele für Kegel

• Eine Eistüte hat die Form eines Kegels.

• Kannst du dich noch an die Schultüte bei deiner Einschulung erinnern? Auch die hat häufig die Form eines Kegels.

Verschiedene Kegel

Es gibt gerade Kegel und schräge Kegel.

Gerade Kegel

Hier siehst du einen geraden Kegel.

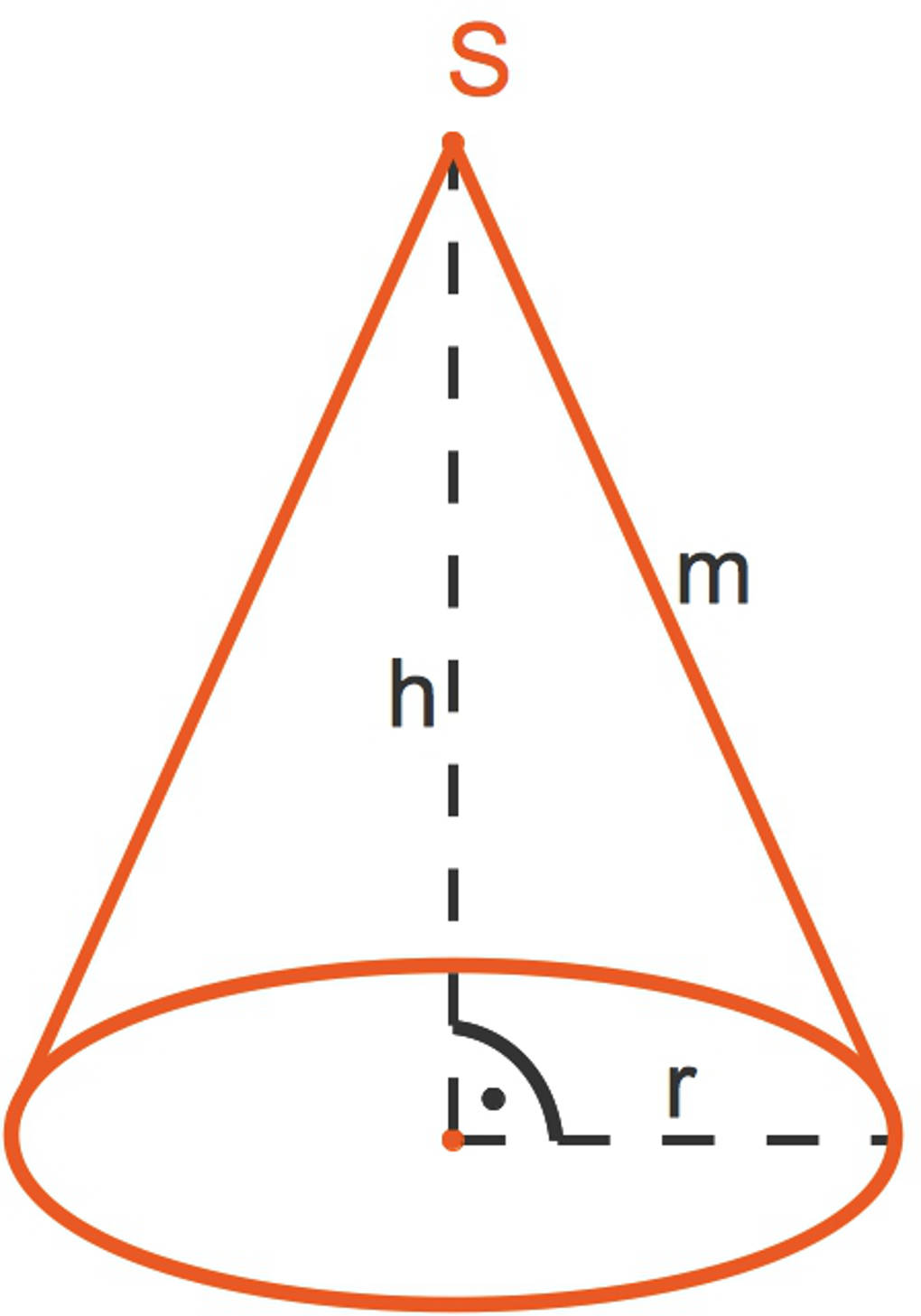
• $S$ ist die Spitze des Kegels. Diese liegt bei einem geraden Kegel genau senkrecht über dem Mittelpunkt des Grundkreises.
• $m$ ist die Mantellinie. Die Mantellinie ist bei einem geraden Kegel immer gleich lang.
• $h$ ist die Höhe des Kegels. Dies ist der Abstand der Spitze zu der Grundfläche. Im Falle des geraden Kegels ist das gerade der Abstand der Spitze zu dem Mittelpunkt des Grundkreises.
• $r$ ist der Radius des Grundkreises.

Schräge Kegel

Hier siehst du einen schrägen Kegel.

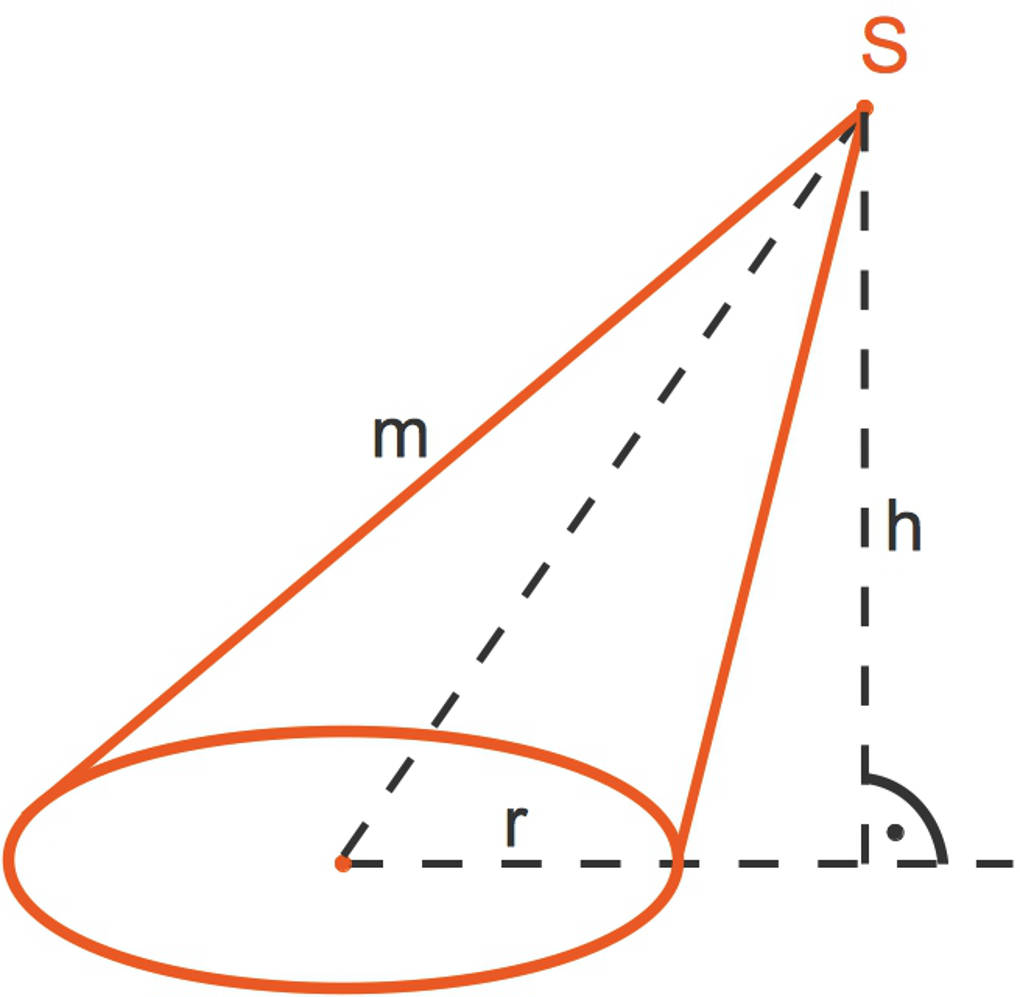
• Im Gegensatz zum geraden Kegel liegt die Spitze nicht senkrecht über dem Mittelpunkt des Grundkreises.
• Die Mantellinien sind bei einem schrägen Kegel nicht gleich lang. Du kannst erkennen, dass die (eingezeichnete) linke Mantellinie länger ist als die rechte.

Zum Beispiel erzeugt eine Lichtquelle einen Lichtkegel. Wenn die Lichtquelle nicht senkrecht nach unten zeigt, entsteht so ein schräger Kegel.

Im Folgenden beschäftigen wir uns mit der Mantelfläche, der Oberfläche und dem Volumen von geraden Kegeln. Bei schrägen Kegeln ist die Berechnung von Mantel- und Oberfläche etwas komplizierter.

Die Mantel- und Oberfläche eines Kegels

Die Oberfläche eines Kegels setzt sich aus der Grundfläche und der Mantelfläche zusammen.

Die Grundfläche

Die Grundfläche eines Kegels ist ein Kreis. Dessen Flächeninhalt kannst du mit Hilfe des Radius $r$ berechnen: $A_G=\pi\cdot r^2$.

Dabei ist $\pi=3,1415...$ die sogenannte Kreiszahl.

Die Mantelfläche

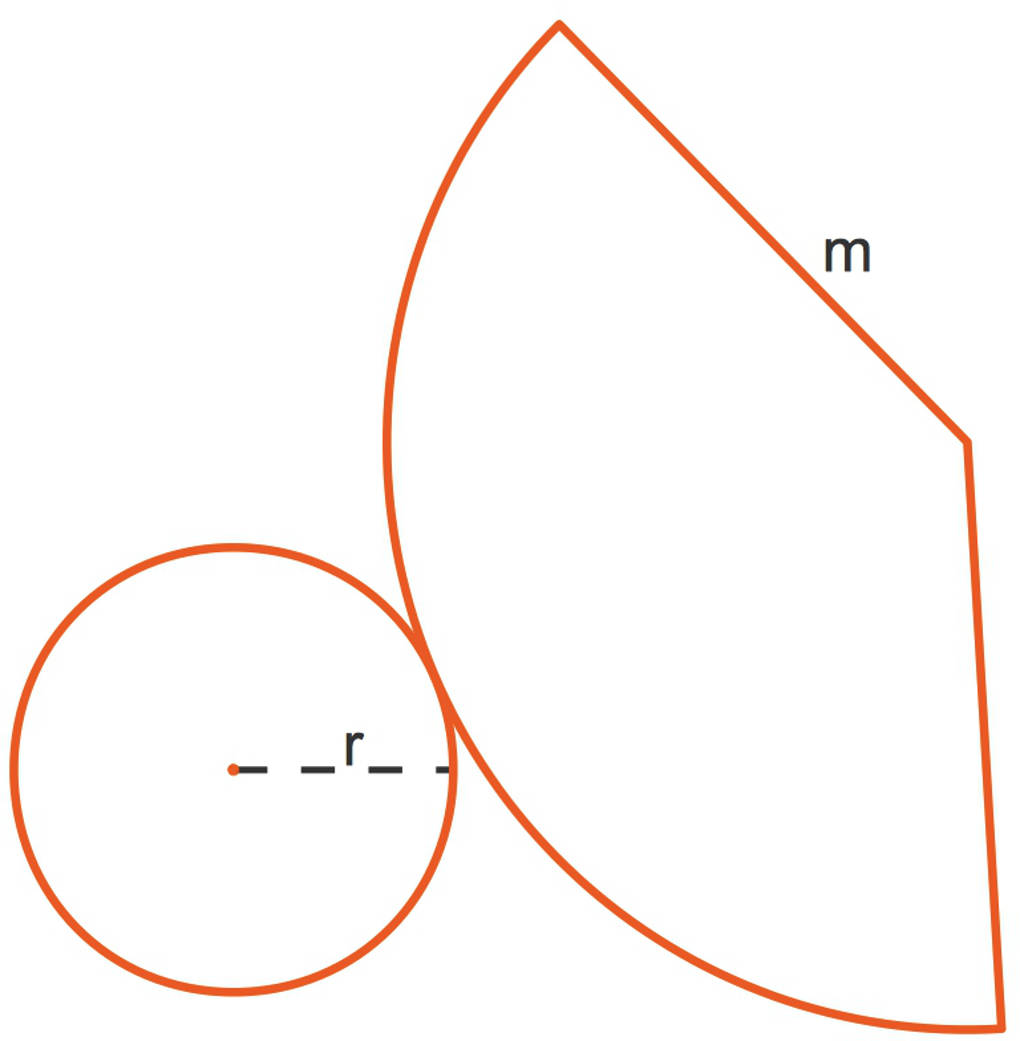
Wie berechnest du die Mantelfäche eines Kegels? Wenn du einen Kegel entlang der Mantellinie aufschneidest, erhältst du den hier zu erkennenden Kreisausschnitt (rechts). Umgekehrt, wenn du einen solchen Kreisausschnitt wieder zusammenlegst, erhältst du einen Kegel. Probiere es doch einmal aus. Der Radius dieses Kreisausschnittes ist die Mantellinie $r_\circ=m$.

Die Mantelfläche $M$ ist die Fläche dieses Kreisausschnittes.

Der Flächeninhalt des gesamten Kreises ist $A_{\circ}=\pi\cdot m^2$. Nun müssen wir uns noch überlegen, wie groß der Anteil des Kreisausschnittes an dem gesamten Kreis ist.

Es gilt

$\frac{M}{A_\circ}=\frac{b}{u_\circ}$,

wobei

• $b$ die Bogenlänge des Kreisausschnittes ist. Diese ist gleich dem Umfang des Grundkreises $u_G=2\cdot \pi\cdot r$.
• Darüber hinaus ist $u_\circ=2\cdot \pi\cdot m$.

Nun können wir dies in die obige Gleichung einsetzen und dann nach $M$ umformen:

$\begin{array}{rclll} \frac{M}{\pi\cdot m^2}&=&\frac{\not 2\cdot \not \pi\cdot r}{\not 2\cdot \not \pi\cdot m}&|&\cdot \pi\cdot m^2\\ M&=&\pi\cdot r\cdot m \end{array}$

Dies ist die gesuchte Mantelfläche.

Die Oberfläche

Die Oberfläche eines Kegels ergibt sich als die Summe von Mantel- und Grundfläche: $O=\pi\cdot r^2+\pi\cdot r\cdot m=\pi\cdot r\cdot (r+m)$.

Das Volumen eines Kegels

Das Volumen eines Kegels kannst du mit Hilfe der folgenden Formel berechnen:

$V=\frac13\cdot\pi\cdot r^2\cdot h$.

$h$ ist die Höhe des Kegels.

Beispiel – Paul bastelt eine Schultüte

Paul isst gerade ein Eis. Beim Anblick seiner kegelförmigen Eistüte denkt er daran, dass er seiner Schwester eine Schultüte basteln will. Diese soll $h=80~cm$ hoch sein und einen Kreis mit dem Radius $r=15~cm$ als Grundfläche haben. Wie viel Pappkarton benötigt er, um die Schultüte zu basteln? Dabei wird der Verschnitt nicht berücksichtigt. Er muss die Mantelfläche eines Kegels berechnen: $M=\pi\cdot r\cdot m$.

Leider kennt er $m$ noch nicht. Er fertigt sich eine Skizze an.

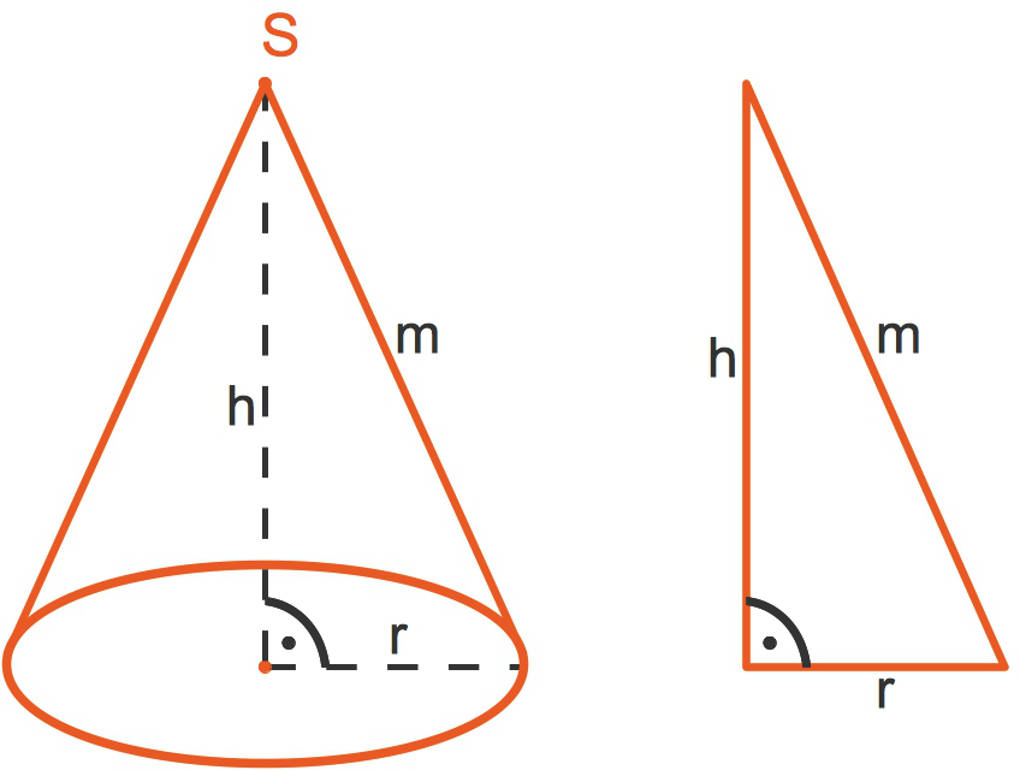
Dabei erkennt er, dass er den Satz des Pythagoras anwenden kann: $h^2+r^2=m^2$.

Er setzt die bekannten Größen ein und zieht die Wurzel:

$m=\sqrt{(80~cm)^2 +(15~cm)^2}=\sqrt{6625~cm^2}\approx 81,40~cm$.

Jetzt kann er die Formel für die Mantelfläche verwenden: $M\approx\pi\cdot (15~cm)\cdot (81,40~cm)\approx 3835,90~cm^2$.

Das weiß er jetzt und kann direkt von der Eisdiele zu dem Bastelladen gehen.

Beispiel – Wie viel Saft passt in ein kegelförmiges Glas?

Ein kegelförmiges Glas mit der Höhe $h=10~cm$ und dem Radius $r=3,5~cm$ wird mit Saft gefüllt. Dieses Mal ist nach dem Volumen gefragt:

$V=\frac13\cdot \pi\cdot (3,5~cm)^2\cdot (10~cm)\approx y128~cm^3$.

Dies entspricht $0,128~L$. So viel passt in das Glas hinein. Wenn du bedenkst, dass das Glas nicht ganz gefüllt wird, passt also etwas mehr als $0,1~L$ hinein.

Der Kegelstumpf

Du erhältst einen Kegelstumpf, wenn du von einem Kegel einen kleineren Kegel an der Spitze parallel zur Grundfläche abschneidest.

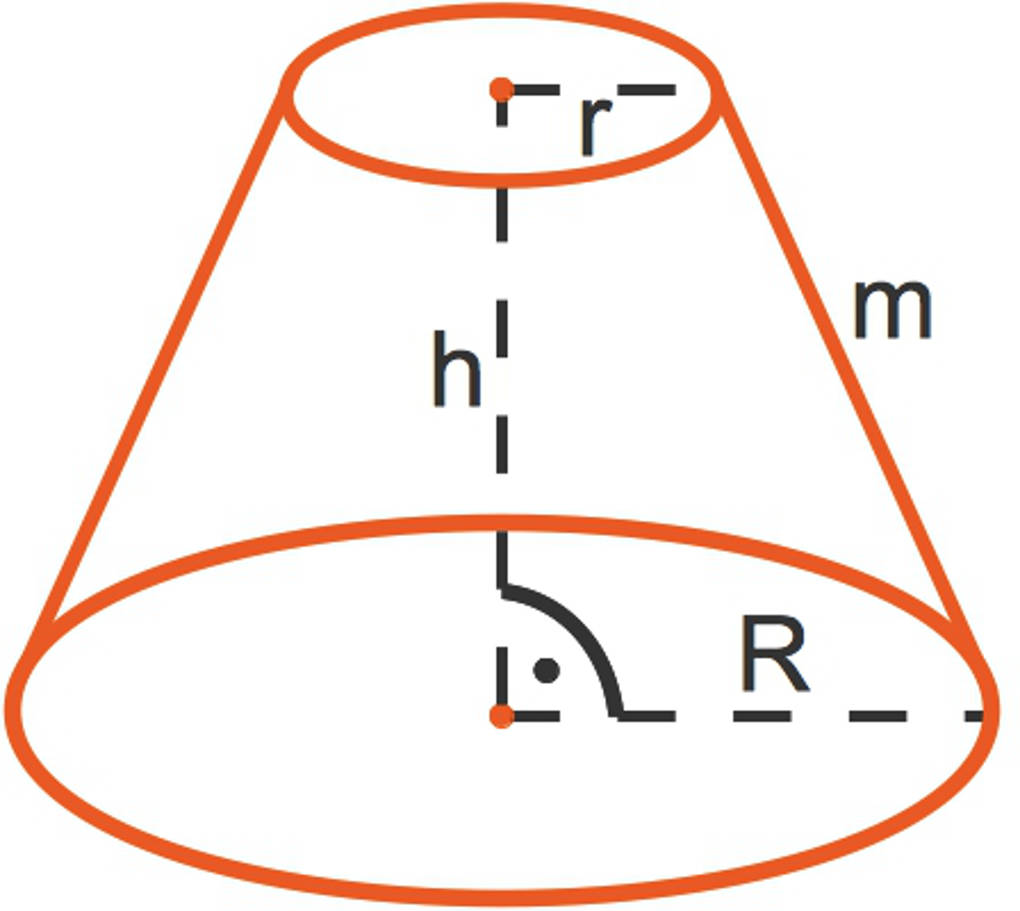
• Ein Kegelstumpf hat im Gegensatz zu einem Kegel neben einer Grundfläche mit dem Radius $R$ auch noch eine Deckfläche mit dem Radius $r < R$.
• Die Höhe des Kegelstumpfes ist $h$, der Abstand von Grund- zu Deckfläche.
• $m$ ist die Mantellinie des Kegelstumpfes.

Die Mantel- und Oberfläche eines Kegelstumpfes

• Der Flächeninhalt der Grundfläche beträgt $A_G=\pi\cdot R^2$ und der
• der Deckfläche $A_D=\pi\cdot r^2$.

Die Mantelfläche kannst du mit der Formel $M=\pi\cdot m\cdot (R+r)$ berechnen.

Die Oberfläche erhältst du, wenn du zu der Mantelfläche die Grund- und Deckfläche addierst: $O=\pi\cdot (R^2+r^2+m\cdot(R+r))$.

Das Volumen eines Kegelstumpfes

Für die Berechnung des Volumens verwendest du die Formel

$V=\frac13\cdot \pi\cdot h\cdot(R^2+R\cdot r+r^2)$.

Beispiel

Beim Schulfest der Schule C. F. Gauss soll eine besonders knifflige Aufgabe gelöst werden.

Ein Kegelstumpf mit einem Volumen von $3500~dm^3$, der Höhe $h=45~dm$ und einem Radius des größeren Kreises, der doppelt so groß ist wie der kleinere, also $R=2r$, soll aus Metallplatten gebaut werden. Der Kegelstumpf soll auf der größeren Grundfläche stehen. Auch diese muss mit dem Material erstellt werden. Nach oben soll der Kegelstumpf offen sein.

Wie viel Material (in $dm^2$) wird für diesen Kegelstumpf benötigt?

Du musst die Mantelfläche berechnen und dazu die Grundfläche addieren.

Es ist $M=\pi\cdot m\cdot (R+r)=3\pi\cdot m\cdot r$. Es sind weder $r$ noch $m$ bekannt.

Mit dem bekannten Volumen

$3500~dm^3=\frac13\cdot \pi\cdot (45~dm)\cdot((2r)^2+r\cdot r+r^2)=6\pi\cdot (15~dm)\cdot r^2$

kann durch Division durch $6\pi\cdot (15~dm)$ und anschließendes Ziehen der Wurzel $r$ berechnet werden:

$r=\sqrt{\frac{3500~dm^3}{6\pi\cdot (15~dm)}}\approx 12,4~dm$.

Damit ist $R=24,8~dm$.

Nun muss noch $m$ berechnet werden. Hierfür verwendest du die folgende Skizze.

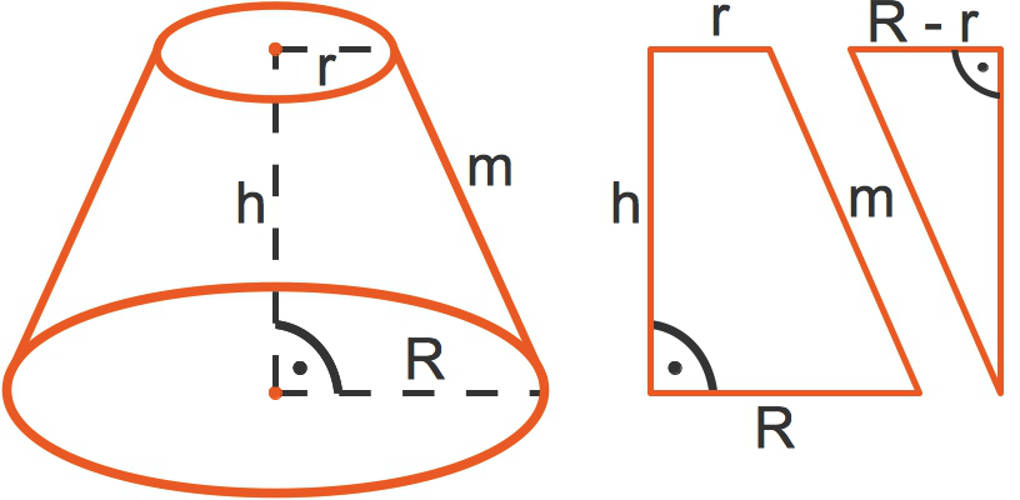
Auch hier kannst du mit dem Satz des Pythagoras die fehlende Größe berechnen:

$m=\sqrt{(R-r)^2+h^2}=\sqrt{(12,4~dm)^2+(45~dm)^2}\approx46,7~dm$.

Nun endlich kann die Mantelfläche berechnet werden:
$M\approx 3\pi\cdot (46,7~dm)\cdot (12,4~dm)\approx5457,7~dm^2$.

Fast fertig. Wenn du noch die Grundfläche $A_G\approx \pi\cdot (24,8~dm)^2=1932,2~dm^2$ addierst, erhältst du den gesuchten Materialaufwand: $5457,7~dm^2+1932,2~dm^2=7389,9~dm^2$.