Flächeninhalt und Umfang von Trapezen
Trapez, Flächeninhalt, Höhe, Formel
Beliebteste Videos
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
Was ist ein Trapez?
Ein Trapez ist eine ebene Figur. Es hat vier Ecken, ist also ein Viereck, und hat auch vier Seiten und vier Winkel.
Was ist das Besondere an einem Trapez? Ein Trapez ist ein Viereck, in welchem mindestens zwei Seiten parallel zueinander sind.
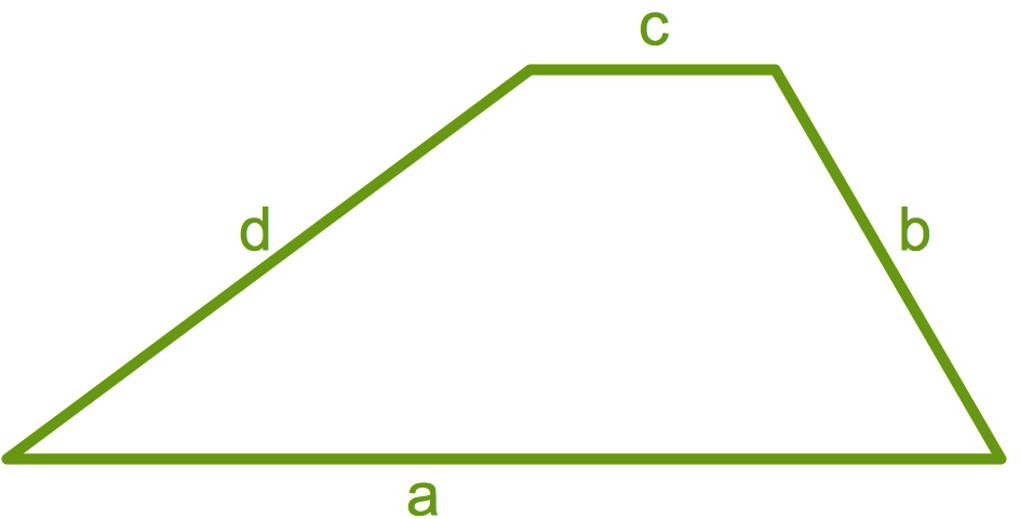
Du kannst hier ein allgemeines Trapez sehen mit den entsprechenden Bezeichnungen der Ecken, Seiten und Winkel.

Die Strecke $h$ bezeichnet die Höhe des Trapezes. Dies ist der Abstand der beiden parallelen Seiten, hier $a$ und $c$, zueinander. Die Höhe steht senkrecht auf der Grundseite $a$.
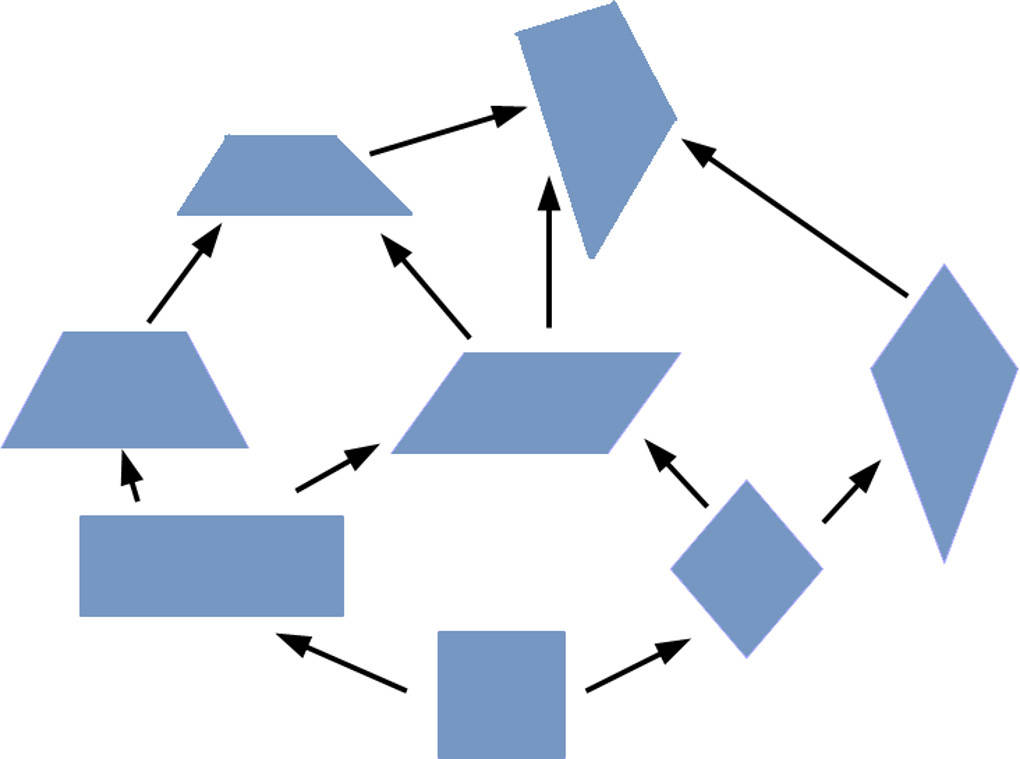
Vierecke, die auch ein Trapez sind.
Welche Vierecke kennst du, die auch (mindestens) zwei zueinander parallele Seiten haben und somit besondere Trapeze sind?
- Beim Rechteck sind die einander gegenüberliegenden Seiten parallel, alle Winkel sind rechte Winkel.
- Das Quadrat ist ein Rechteck, in welchem alle Seiten gleich lang sind.
- Beim Parallelogramm sind die einander gegenüberliegenden Seiten parallel, aber die Winkel müssen nicht rechte Winkel sein.
- Die Raute (oder auch der Rhombus) ist ein Parallelogramm, in welchem alle Seiten gleich lang sind.
Den Zusammenhang zwischen den Vierecken kannst du in dem Haus der Vierecke sehen.
Eigenschaften der Innenwinkel
- Die Summe der Innenwinkel eines Vierecks beträgt $360^\circ$. Dies gilt natürlich auch für das Trapez.
- Die Summe zweier benachbarter Winkel, die an den nicht parallelen Seiten anliegen, ist immer $180^\circ$, also
$\quad~~~\alpha+\delta=\beta+\gamma=180^\circ$
.
Spezielle Trapeze
- Es gibt Trapeze, bei welchen die Seiten $b$ und $d$ gleich lang sind. Solche Trapeze werden als gleichschenklige Trapeze oder symmetrische Trapeze bezeichnet.
- Wenn einer der Winkel ein rechter Winkel ist, dann spricht man von einem rechtwinkligen Trapez. Übrigens: Wegen der Eigenschaft, dass die Summe der benachbarten Winkel $180^\circ$ beträgt, ist auch der benachbarte Winkel ein rechter Winkel.
Der Umfang eines Trapezes
Für den Umfang eines Trapezes addierst du die Längen aller vier Seiten:
$\quad~~~U=a+b+c+d$
Beispiel
Herr Gockel möchte um sein Grundstück einen Zaun bauen. Das Grundstück hat die Form eines gleichschenkligen Trapezes mit den Seitenlängen $a=40~m$, $b=d=10~m$ und $c=24~m$. Wie lang ist der Zaun insgesamt?
Er muss die einzelnen Längen addieren: $40~m+2\cdot 10~m+24~m=84~m$.
Der Zaun hat also insgesamt eine Länge von $84~m$.
Die Fläche eines Trapezes
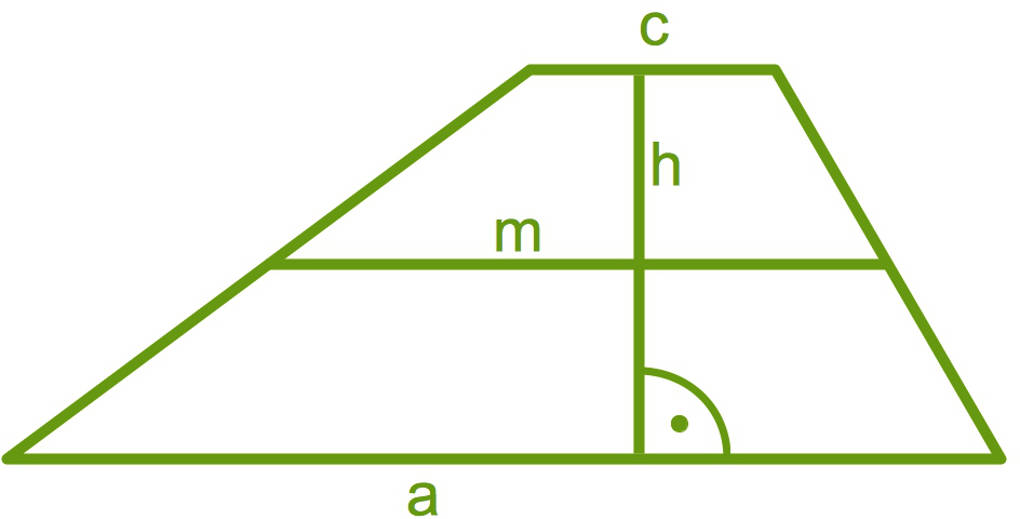
Hier siehst du die Größen in einem Trapez, welche du für die Flächenberechnung benötigst:
 .
.
Der Flächeninhalt eines Trapezes ist gegeben durch
$\quad~~~A=\frac{a+c}2\cdot h$.
.
Diese Formel findest du auch oft so
$\quad~~~A=m\cdot h$,
, wobei
$\quad~~~m=\frac{a+c}2$
die Länge der Strecke ist, welche sich genau in der Mitte zwischen den beiden parallelen Seiten befindet.
Herleitung der Flächenformel
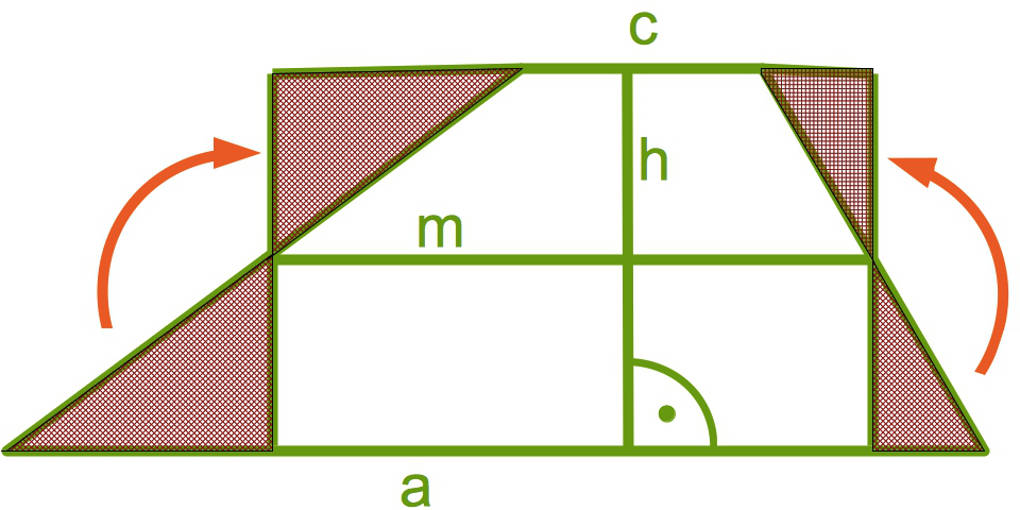
Um diese Formel für den Flächeninhalt herzuleiten, schaue dir dieses Bild an:
 .
.
- Stell dir vor, du würdest bei einem Trapez das Dreieck unten links ausschneiden. Dieses Dreieck fügst du, wie in dem Bild zu sehen, oben links an das Trapez an.
- Das machst du genauso mit dem Dreieck unten rechts.
- Du erhältst dann ein flächengleiches Rechteck mit den Seitenlängen $m$ und $h$.
- Der Flächeninhalt dieses Rechtecks ist $A_{\text{Rechteck}}=m\cdot h$.
Da $m=\frac{a+c}2$ gilt, ist damit die Formel für den Flächeninhalt eines Trapezes mit $A=\frac{a+c}2\cdot h$ nachgewiesen.
Beispiel
Herr Gockel weiß, dass sein Grundstück den Flächeninhalt $A=192~m^2$ hat. Das Grundstück hat die Form eines gleichschenkligen Trapezes. Eine der beiden parallelen Seiten ist $a=40~m$ und die Höhe des Trapez beträgt $h=6~m$. Er möchte an die beiden parallelen Seiten eine Hecke pflanzen. Wie lang wird diese Hecke?
Herr Gockel kennt also bereits eine der beiden parallelen Seiten. Er muss nun noch die fehlende Größe herleiten. Er verwendet hierfür die Formel zur Berechnung des Flächeninhaltes
$\quad~~~A=\frac{a+c}2\cdot h$
und setzt dort die bereits bekannten Größen ein
$\quad~~~192~m^2=\frac{40~m+c}2\cdot 6~m$.
.
Diese Gleichung formt er nach $c$ um.
$\begin{array}{rclll} 192~m^2&=&\frac{40~m+c}{2} \cdot 6~m&&\\ \\ 192~m^2&=&(40~m+c)\cdot 3~m&|&:(3~m)\\ \\ 64~m&=&40~m+c&|&-40~m\\ \\ 24~m&=&c&&\\ \\ \end{array}$
Die Gesamtlänge der Hecke beträgt dann also $40~m+24~m=64~m$.
Alle Videos zum Thema
Videos zum Thema
Flächeninhalt und Umfang von Trapezen (3 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Flächeninhalt und Umfang von Trapezen (3 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Primzahlen
- Geometrische Lagebeziehungen
- Rechteck
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Quadrat
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Was Ist Eine Viertelstunde
- Prisma
- Mitternachtsformel
- Grundrechenarten Begriffe
- Dreiecksarten
- Quader
- Satz Des Pythagoras
- Dreieck Grundschule
- Erste Binomische Formel
- Kreis
- Standardabweichung
- Flächeninhalt
- Volumen Kugel
- Zahlen In Worten Schreiben
- Meter
- Orthogonalität
- Schriftlich Multiplizieren
- Brüche Multiplizieren
- Potenzgesetze
- Distributivgesetz
- Flächeninhalt Dreieck
- Rationale Zahlen
- Volumen Berechnen
- Brüche Addieren
- Kongruenz
- Exponentialfunktion
- Scheitelpunktform
- Logarithmus
- Erwartungswert
- Skalarprodukt
- Primfaktorzerlegung
- Quadratische Ergänzung
- Zinseszins
- Geradengleichung Aus Zwei Punkten Bestimmen
- Sinusfunktion





 Das Trapez
Das Trapez
 Flächeninhalt und Umfang des Trapezes
Flächeninhalt und Umfang des Trapezes
 Trapez – Fehlende Größen berechnen
Trapez – Fehlende Größen berechnen









