Termumformungen – Überblick
Terme sind Rechenausdrücke. In diesen kommen Zahlen, Variablen und Rechenzeichen vor. Oftmals genügt es nicht, einen Term aufzustellen, sondern du musst diesen Term auch noch vereinfachen, also umformen.
Beliebteste Videos
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Was ist ein Term?
- Was sind Termumformungen?
- Die Addition oder Subtraktion von Termen
- Die Multiplikation oder Division von Termen
- Das Kommutativgesetz der Addition
- Das Kommutativgesetz der Multiplikation
- Vorzeichenregeln
- Das Distributivgesetz
- Das Assoziativgesetz der Addition
- Das Assoziativgesetz der Multiplikation
- Die binomischen Formeln
- Beispiele
Was ist ein Term?
Ein Term ist ein sinnvoller Rechenausdruck, in welchem
- Zahlen,
- Variablen,
- Rechenzeichen und
- Klammern vorkommen.
In einem Term kommen KEINE
- Gleichheitszeichen ($=$) oder
- Relationszeichen ($>$, $\ge$, $<$, $\le$) vor.
Was bedeutet „sinnvoll“? Wenn du für die Variablen Zahlen einsetzt, kannst du den Wert des Terms berechnen.
Beispiele
- Eine Zahl oder eine Variable können durchaus alleine stehen. In beiden Fälle würde es sich um einen Term handeln, wie zum Beispiel bei $4$ oder $x$. Ein Rechenzeichen allein ist kein Term.
- Ein Rechenzeichen kann auch als Vorzeichen verwendet werden, zum Beispiel $-4$ für eine negative Zahl. Auch dies ist ein Term.
- Allerdings ist $4-$ kein Term.
- $4-x$ ist ein Term. Er besteht aus der Zahl $4$, dem Rechenzeichen $-$ und der Variablen $x$. Wenn du zum Beispiel für $x$ den Wert $3$ einsetzt, erhältst du $4-3=1$.
- Terme können auch durchaus etwas umfangreicher sein. Damit beschäftigen wir uns im Folgenden.
Was sind Termumformungen?
Wir schauen uns zunächst an, was unter ergebnisgleichen Termen verstanden wird. Zwei Terme heißen ergebnisgleich, wenn die Terme, egal welche Werte für die Variablen eingesetzt werden, immer das gleiche Ergebnis haben.
Alle Umformungen eines Terms in einen ergebnisgleichen Term heißen Termumformungen. Du kannst auch sagen, dass der Term vereinfacht oder verändert wird.
Bei Termumformungen musst du verschiedene Regeln befolgen:
- Der Wert des Terms muss gleich bleiben.
- Klammern werden zuerst durchgeführt.
- Es gilt „Punkt geht vor Strich“.
Die Addition oder Subtraktion von Termen
Merke dir: Du kannst nur Terme addieren oder subtrahieren, die gleichartig sind. Zwei Terme heißen gleichartig, wenn sie in den Variablen und dem Exponenten überein stimmen. Die Koeffizienten, also die Faktoren vor dem Term, können verschieden sein.
- $2x$ und $3x$ sind gleichartige Terme. Es gilt $2x+3x=(2+3)x=5x$. Du addierst hier die Koeffizienten. Wenn du zum Beispiel zwei Handys hast und noch drei Handys hinzukommen, dann hast du insgesamt fünf Handys.
- $2x$ und $3y$ sind nicht gleichartige Terme. Du kannst also $2x+3y$ nicht weiter vereinfachen.Wenn du zum Beispiel zwei Handys hast und drei Taschenrechner hinzukommen, dann hast du insgesamt zwei Handys und drei Taschenrechner.
- $4x^2+3x^2=(4+3)x^2=7x^2$, da die beiden Summanden gleichartige Terme sind.
- $4x^2+3x^3$ lässt sich nicht weiter vereinfachen, da die beiden Summanden nicht gleichartige Terme sind. Hier sind die Exponenten verschieden.
Die Multiplikation oder Division von Termen
Du kannst beliebige Terme multiplizieren oder dividieren. Beim Dividieren kannst du gegebenenfalls kürzen:
- $(3x)\cdot (6y)=18xy~~$ Üblicherweise schreibst du die Faktoren in der Reihenfolge, $~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~$ wie sie im Alphabet vorkommen.
- $\frac{3x}{6y}=\frac{3x}{6 y}=\frac{x}{2y}$ für alle $y>0$
Das Kommutativgesetz der Addition
Das Kommutativitätsgesetz besagt, dass du die Reihenfolge bei der Addition vertauschen darfst, also $a+b=b+a$. Es wird auch Vertauschungsgesetz genannt.
Hier siehst du ein Beispiel, wie du mit Hilfe des Kommutativitätsgesetzes einen Term vereinfachen kannst: $7x+3y+2x+y+8x-4y-5x$.
- Vertausche zunächst die Reihenfolge so, dass gleichartige Terme beieinander stehen. Achte darauf, das Vorzeichen mitzunehmen: $7x+3y+2x+y+8x-4y-5x=7x+2x+8x-5x+3y+y-4y$.
- Nun kannst du die Koeffizienten addieren oder subtrahieren:
$\begin{array}{rcl} ~~7x+2x+8x-5x+3y+y-4y&=&(7+2+8-5)x+(3+1-4)y\\ &=&12x \end{array}$
Das Kommutativgesetz der Multiplikation
Dieses Kommutativitätsgesetz besagt, dass du die Reihenfolge bei der Multiplikation vertauschen darfst, also $a\cdot b=b\cdot a$.
Vorzeichenregeln
- Die Addition eines Terms mit einem negativen Vorzeichen: $a+(-b)=a-b$.
- Die Subtraktion eines Terms mit einem negativen Vorzeichen: $a-(-b)=a+b$.
- Die Multiplikation eines Terms mit einem negativen Vorzeichen: $(-a)\cdot b=-(a\cdot b)$.
- Die Multiplikation zweier Terme mit negativem Vorzeichen: $(-a)\cdot (-b)=a\cdot b$.
- Die Division eines Terms mit einem negativen Vorzeichen: $\frac{(-a)} b=-\frac ab$.
- Die Division zweier Terme mit negativem Vorzeichen: $\frac{-a}{-b}=\frac ab$.
Das Distributivgesetz
Das Distributivgesetz besagt, wie die Multiplikation von Klammertermen durchgeführt wird: $a\cdot (b+c)=a\cdot b+a\cdot c$.
Du siehst, du multiplizierst jeden Term in der Klammer mit dem Term vor der Klammer.
Dies wird auch als Ausmultiplizieren bezeichnet. Umgekehrt kannst du auch ausklammern $a \cdot b+a \cdot c=(a+b) \cdot c$, da in beiden Summanden der gemeinsame Faktor $x$ vorkommt.
Spezialfälle dieser Regeln sind Vorzeichen vor Klammern:
- $+(a+b)=a+b~~~~$ Hier kannst du die Klammern weglassen.
- $-(a+b)=-a-b ~$ Du musst in der Klammer jeweils das Vorzeichen umdrehen.
Du kannst auch kompliziertere Multiplikationen mit dem Distributivgesetz durchführen: $(x+2)\cdot (x+3)$.
- Multipliziere $(x+2)$ mit jedem Term in der rechten Klammer: $(x+2)\cdot (x+3)=(x+2)\cdot x+(x+2)\cdot 3$.
- Nun kannst du wieder das Distributivgesetz anwenden: $(x+2)\cdot x+(x+2)\cdot 3=x\cdot x+2\cdot x+x\cdot 3+2\cdot 3$.
- Nun kannst du das Kommutativgesetz der Multiplikation verwenden und zusammenfassen: $x\cdot x+2\cdot x+x\cdot 3+2\cdot 3=x^2+2x+3x+6$.
- Übrigens kannst du statt $2\cdot x$ auch $2x$ schreiben.
- Addieren oder subtrahieren kannst du nur gleichartige Terme: $x^2+2x+3x+6=x^2+5x+6$.
- Diesen Term kannst du nicht weiter vereinfachen.
Das Assoziativgesetz der Addition
Das Assoziationsgesetz der Addition, besagt dass du die Klammerung der Addition auch tauschen kannst: $(a+b)+c=a+(b+c)$.
Üblicherweise rechnest du von links nach rechts, ebenso wie du liest.
Beispiel: $122x+(8x+12x)=122x+20x=242x=130x+12x=(122x+8x)+12x$
Das Assoziativgesetz der Multiplikation
Du kannst die Klammerung bei der Multiplikation tauschen: $(a\cdot b)\cdot c=a\cdot (b\cdot c)$.
Beispiel: $122x\cdot(2\cdot 5)=122x\cdot 10=1220x=244x\cdot 5=(122x\cdot 2)\cdot 5$
Die binomischen Formeln
Die binomischen Formeln sind Spezialfälle des Distributivgesetzes und eine komplexere Termumformung. Es werden jeweils zwei Binome miteinander multipliziert. Daher kommt der Name:
- Die 1. binomische Formel $(a+b)^2=a^2+2ab+b^2$.
- Die 2. binomische Formel $(a-b)^2=a^2-2ab+b^2$.
- Die 3. binomische Formel $(a+b)\cdot (a-b)=a^2-b^2$.
Beispiele
Beispiel 1
Addiere zu dem Dreifachen einer unbekannten Zahl das Doppelte der um zwei verringerten Zahl.
Die unbekannte Zahl sei $x$.
- Das Dreifache der Zahl: $3x$.
- Die um zwei verringerte Zahl: $x-2$.
- Das Doppelte der um zwei verringerten Zahl: $2(x-2)$.
- Die Addition führt zu: $3x+2(x-2)$.
Diesen Term kannst du noch vereinfachen:
- Wende das Distributivgesetz an: $3x+2(x-2)=3x+2x-4$.
- Addiere die gleichartigen Terme: $3x+2x-4=5x-4$.
- Diesen Term kannst du nicht weiter vereinfachen.
Im Folgenden siehst du noch zwei Beispiele für das Aufstellen und anschließende Umformen von Termen:
Beispiel 2
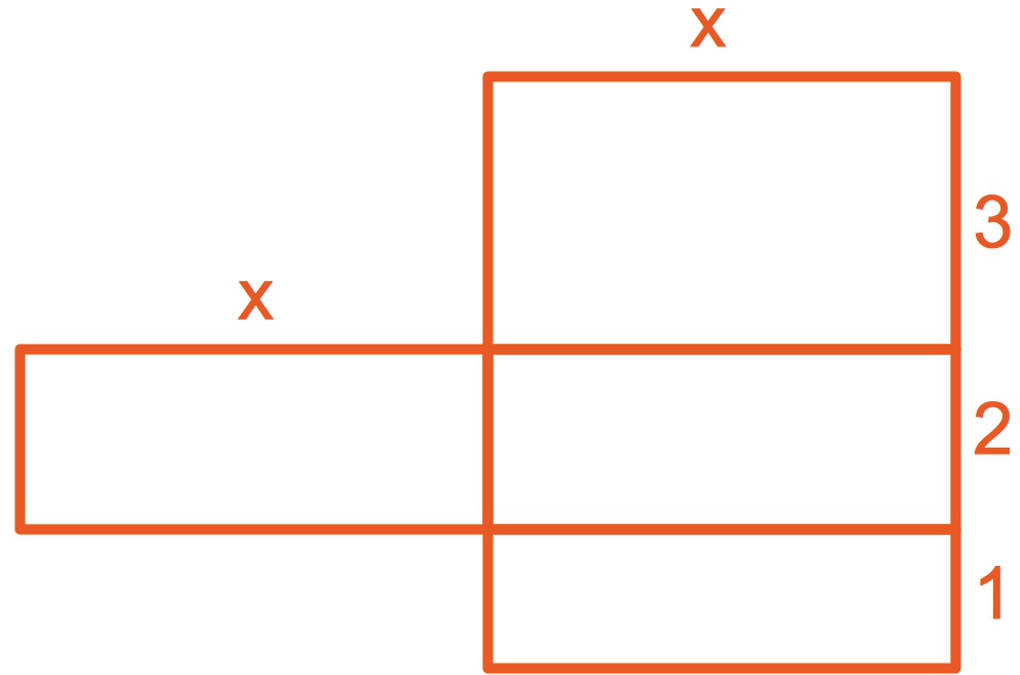
Gesucht ist ein Term, welcher den Inhalt der abgebildeten Fläche in Abhängigkeit von $x$ angibt.
- Du siehst ein Rechteck mit den Seitenlängen $x$ und $3$, also dem Flächeninhalt $3x$.
- Zwei Rechtecke haben die Seitenlängen $x$ und $2$, also insgesamt den Flächeninhalt $2\cdot 2x=4x$.
- Das untere Rechteck hat die Seitenlängen $x$ und $1$, also den Flächeninhalt $1 \cdot x=x$.
- Die jeweiligen Flächeninhalte musst du nun addieren: $3x+4x+x=(3+4+1)x=8x$.
- Nun kannst du verschiedene Werte für $x$ einsetzen und erhältst den entsprechenden Flächeninhalt.
- Die Aufgabe könnte auch weitergehen. Wie groß muss $x$ sein, damit der gesamte Flächeninhalt $16$ beträgt? Dies führt zu der Gleichung $8x=16$, welche du dadurch löst, dass du auf beiden Seiten durch $2$ dividierst. Du erhältst $x=2$.
Beispiel 3
Hier kannst Termumformungen an einem komplexeren Beispiel üben: $3(x+2)^2-x(2x+3)-(x+4)\cdot (x-1)$
Mit Hilfe der 1. binomischen Formel erhältst du $(x+2)^2=x^2+4x+4$.
Wende das Distributivgesetz dreimal an:
- $3(x^2+4x+4)=3x^2+12x+12$
- $-x(2x+3)=-2x^2-3x$: Achte unbedingt auf das Vorzeichen.
- $-(x+4)\cdot (x-1)=-x^2-4x+x+4=-x^2-3x+4$
Nun kannst du die Terme einsetzen:
$\begin{array}{rcl} &&3(x+2)^2-x(2x+3)-(x+4)\cdot (x-1)\\ &=&3x^2+12x+12-2x^2-3x-x^2-3x+4 \end{array}$
Vertausche die Reihenfolge so, dass gleichartige Terme beieinander stehen:
$\begin{array}{rcl} &&3x^2+12x+12-2x^2-3x-x^2-3x+4\\ &=&3x^2-2x^2-x^2+12x-3x-3x+12+4\end{array}$
Zuletzt kannst du noch ausrechnen, also gleichartige Terme addieren oder subtrahieren:
$3x^2-2x^2-x^2+12x-3x-3x+12+4=6x+16$.
Alle Videos zum Thema
Videos zum Thema
Termumformungen – Überblick (6 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Termumformungen – Überblick (6 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Primzahlen
- Geometrische Lagebeziehungen
- Rechteck
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Quadrat
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Was Ist Eine Viertelstunde
- Prisma
- Mitternachtsformel
- Grundrechenarten Begriffe
- Dreiecksarten
- Quader
- Satz Des Pythagoras
- Dreieck Grundschule
- Erste Binomische Formel
- Kreis
- Standardabweichung
- Flächeninhalt
- Volumen Kugel
- Zahlen In Worten Schreiben
- Meter
- Orthogonalität
- Schriftlich Multiplizieren
- Brüche Multiplizieren
- Potenzgesetze
- Distributivgesetz
- Flächeninhalt Dreieck
- Rationale Zahlen
- Volumen Berechnen
- Brüche Addieren
- Kongruenz
- Exponentialfunktion
- Scheitelpunktform
- Logarithmus
- Erwartungswert
- Skalarprodukt
- Primfaktorzerlegung
- Quadratische Ergänzung
- Zinseszins
- Geradengleichung Aus Zwei Punkten Bestimmen
- Sinusfunktion











 Termumformungen ohne Variablen
Termumformungen ohne Variablen
 Termumformungen mit Variablen
Termumformungen mit Variablen
 Termumformungen (Übungsvideo)
Termumformungen (Übungsvideo)
 Termumformungen mit mehreren Variablen
Termumformungen mit mehreren Variablen
 Gleichungen mit Brüchen vereinfachen
Gleichungen mit Brüchen vereinfachen
 Terme mit unterschiedlichen Variablen zusammenfassen
Terme mit unterschiedlichen Variablen zusammenfassen









