Seitenlängen, Diagonalen und Winkel in Vierecken
Kennst du das Haus der Vierecke? In diesem sind die verschiedenen Vierecke erklärt. Dabei lernst du insbesondere, welche Eigenschaften welches Viereck ausmachen.
Beliebteste Videos
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Das Haus der Vierecke
- Die Innenwinkel in einem Viereck
- Innenwinkel im Parallelogramm
- Diagonalabschnitte im Parallelogramm
- Schnittwinkel der Diagonalen im Drachenviereck
Das Haus der Vierecke
Ein Viereck ist eine ebene Figur. Ein Viereck hat, wie du an dem Namen bereits erkennen kannst, vier Ecken.
Es gibt verschiedene Vierecke. Diese kannst du im Haus der Vierecke sehen.
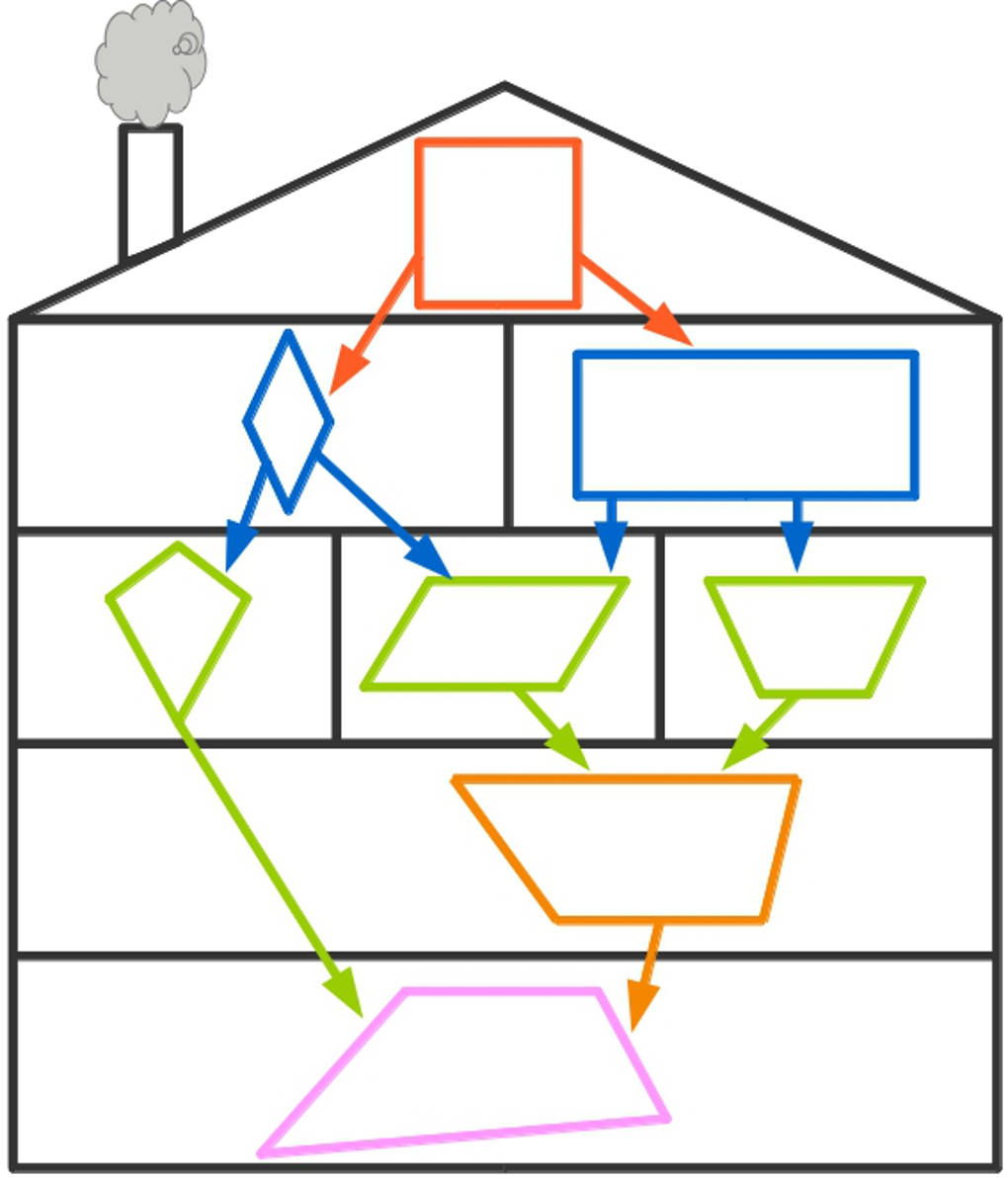
Lass uns einmal ganz oben beginnen.
- Das Quadrat: Es zeichnet sich dadurch aus, dass alle vier Seiten gleich lang sind. Die jeweils gegenüberliegenden Seiten sind parallel zueinander. Jeweils zwei Seiten schließen einen rechten Winkel ein. Jedes Quadrat ist auch eine Raute und ein Rechteck. Dies wird hier durch die Pfeile angedeutet.
- Die Raute: Sie wird auch Rhombus genannt. Du findest sie in dem Zimmer links unter dem Quadrat. Bei einer Raute sind auch alle Seiten gleich lang und die jeweils einander gegenüberliegenden Seiten sind parallel zueinander. Die Winkel sind allerdings keine rechten Winkel mehr. Jede Raute ist auch ein Drachenviereck oder ein Parallelogramm.
- Das Rechteck: Es wohnt in dem Zimmer rechts unter dem Quadrat und unterscheidet sich von diesem dadurch, dass nur die einander gegenüberliegenden Seiten gleich lang sind. Jedes Rechteck ist auch ein Parallelogramm oder ein gleichschenkliges Trapez.
- Das Drachenviereck: Es wohnt in dem Zimmer ganz links unter der Raute. Die beiden einander anliegenden Seiten sind gleich lang. Jedes Drachenviereck ist auch ein allgemeines Viereck.
- Das Parallelogramm wohnt in dem mittleren Zimmer. Die einander gegenüberliegenden Seiten sind parallel zueinander und gleich lang. Was unterscheidet ein Parallelogramm von einem Rechteck? Die Winkel sind keine rechten Winkel. Jedes Parallelogramm ist auch ein Trapez.
- Das gleichschenklige Trapez wohnt in dem rechten Zimmer unter dem Rechteck. Es ist ein besonderes Trapez. Die beiden Schenkel sind gleich lang.
- Das Trapez wohnt unter den grünen Vierecken. In einem Trapez sind (mindestens!) zwei Seiten parallel zueinander. Jedes Trapez ist auch ein allgemeines Viereck.
- Ganz unten wohnt das allgemeine Viereck.
Siehst du den Schornstein? Auch dieser ist ein Viereck. Na, kannst du nun sagen, welches der oben genannten Vierecke der Schornstein ist? Richtig, ein Trapez.
Die Innenwinkel in einem Viereck
Du kennst doch sicher noch den Winkelsummensatz: Die Summe der Innenwinkel eines beliebigen Dreiecks beträgt $180^\circ$.
Nun schauen wir uns an, wie groß die Summe der Innenwinkel eines beliebigen Vierecks ist. Schaue dir hierfür dieses Viereck an.
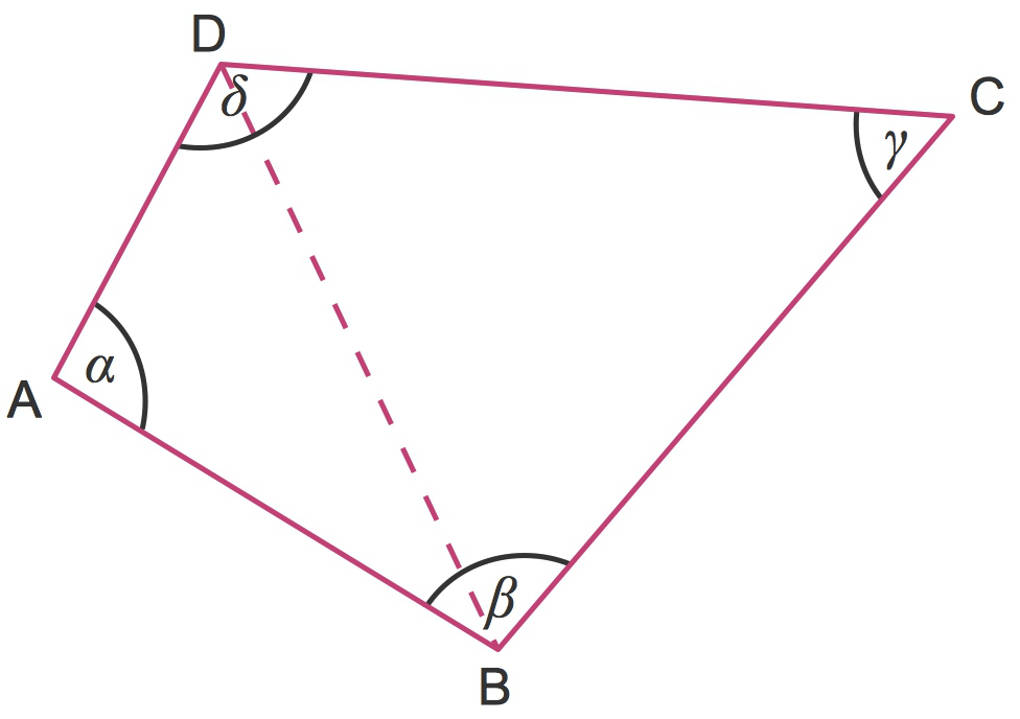
Durch die gestrichelte Linie wird das Viereck $ABCD$ in zwei Dreiecke $ABD$ und $BCD$ geteilt. In jedem dieser Dreiecke gilt, dass die Summe der Innenwinkel $180^\circ$ beträgt. Somit gilt für das Viereck, dass die Summe der Innenwinkel
$\alpha+\beta+\gamma+\delta=2\cdot 180^\circ=360^\circ$
beträgt. Dies gilt für jedes beliebige Viereck.
Innenwinkel im Parallelogramm
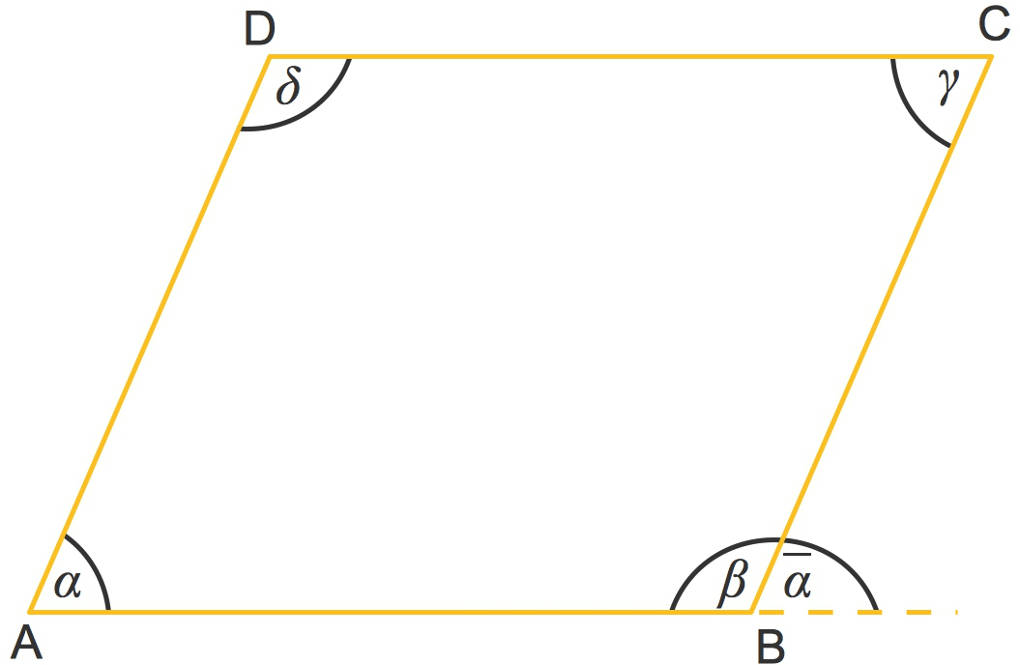
Da die untere Seite des Parallelogramms von zwei parallelen Geraden geschnitten wird, sind die beiden Winkel $\alpha$ sowie $\bar{\alpha}$ Stufenwinkel und somit gleich groß $\alpha=\bar{\alpha}$.
Damit kannst du folgern, dass $\beta+\alpha=180^\circ$ ist. Dies gilt übrigens für jedes Paar benachbarter Innenwinkel in einem Parallelogramm.
$\alpha+\beta=\beta+\gamma=\gamma+\delta=\delta+\alpha=180^\circ$.
Wenn du zwei gegenüberliegende Punkte verbindest, erhältst du eine Diagonale.
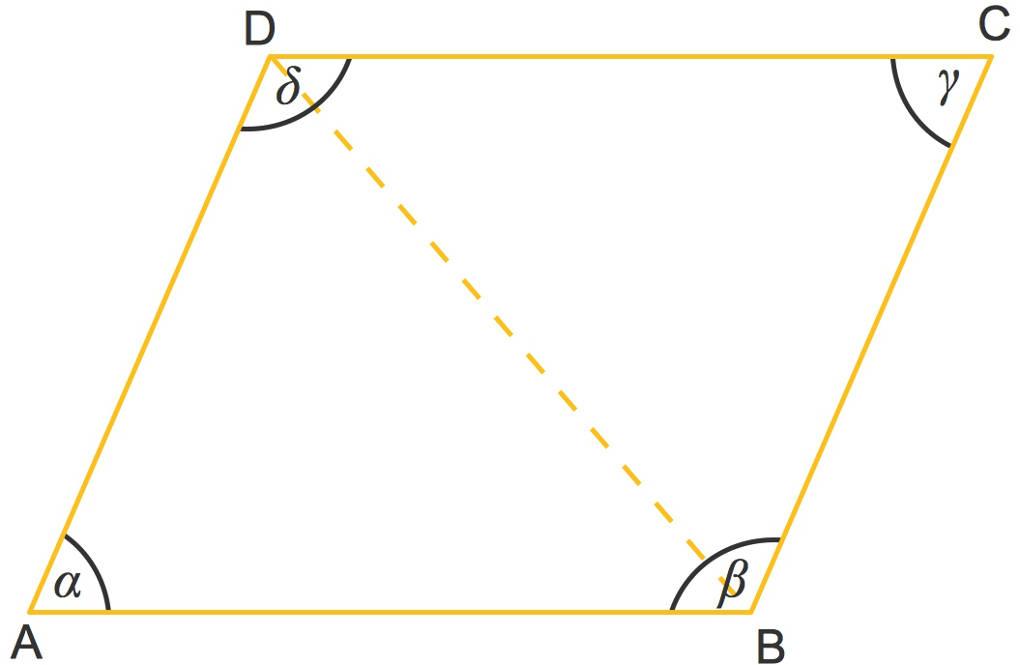
Diese Diagonale teilt das Parallelogramm $ABDC$ in zwei kongruente Dreiecke $ABD$ sowie $BCD$, da alle drei Seiten gleich lang sind. Dies ist der Kongruenzsatz SSS.
Damit stimmen auch die Winkel überein und somit gilt $\alpha=\gamma$. Ebenso ist $\beta=\delta$.
Das bedeutet, dass zwei einander gegenüberliegende Winkel in einem Parallelogramm immer gleich groß sind.
Diese Aussagen gelten natürlich auch für jede Raute, für jedes Rechteck und für jedes Quadrat.
Diagonalabschnitte im Parallelogramm
Betrachten wir nun die Diagonalabschnitte im Parallelogramm.
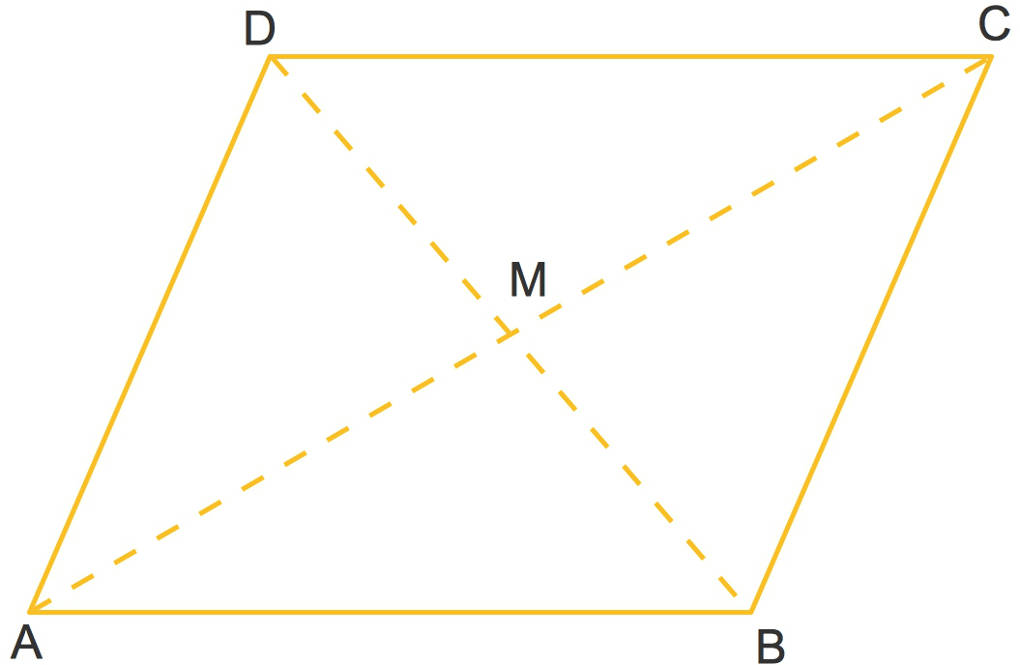
Wir schauen uns die beiden Dreiecke $ABM$ sowie $CDM$ an:
- Die Winkel $\angle(BAM)$ sowie $\angle(DCM)$ stimmen überein, da sie Wechselwinkel sind.
- Ebenso stimmen die Winkel $\angle(ABM)$ sowie $\angle(CDM)$ überein.
- Die Strecken $\overline{AB}$ sowie $\overline{CD}$ sind gleich lang.
Da also die beiden Dreiecke in einer Seite und den anliegenden Winkeln übereinstimmen, sind sie kongruent. Dies ist der Kongruenzsatz WSW.
Somit sind die Strecken $\overline{AM}$ und $\overline{MC}$ gleich lang. Die Strecken $\overline{BM}$ und $\overline{MD}$ sind ebenfalls gleich lang.
Das bedeutet, dass sich die beiden Diagonalen genau in der Mitte schneiden.
Diese Aussage gilt ebenso für jede Raute, für jedes Rechteck und für jedes Quadrat.
Schnittwinkel der Diagonalen im Drachenviereck
In welchem Winkel schneiden sich die Diagonalen in einem Drachenviereck?
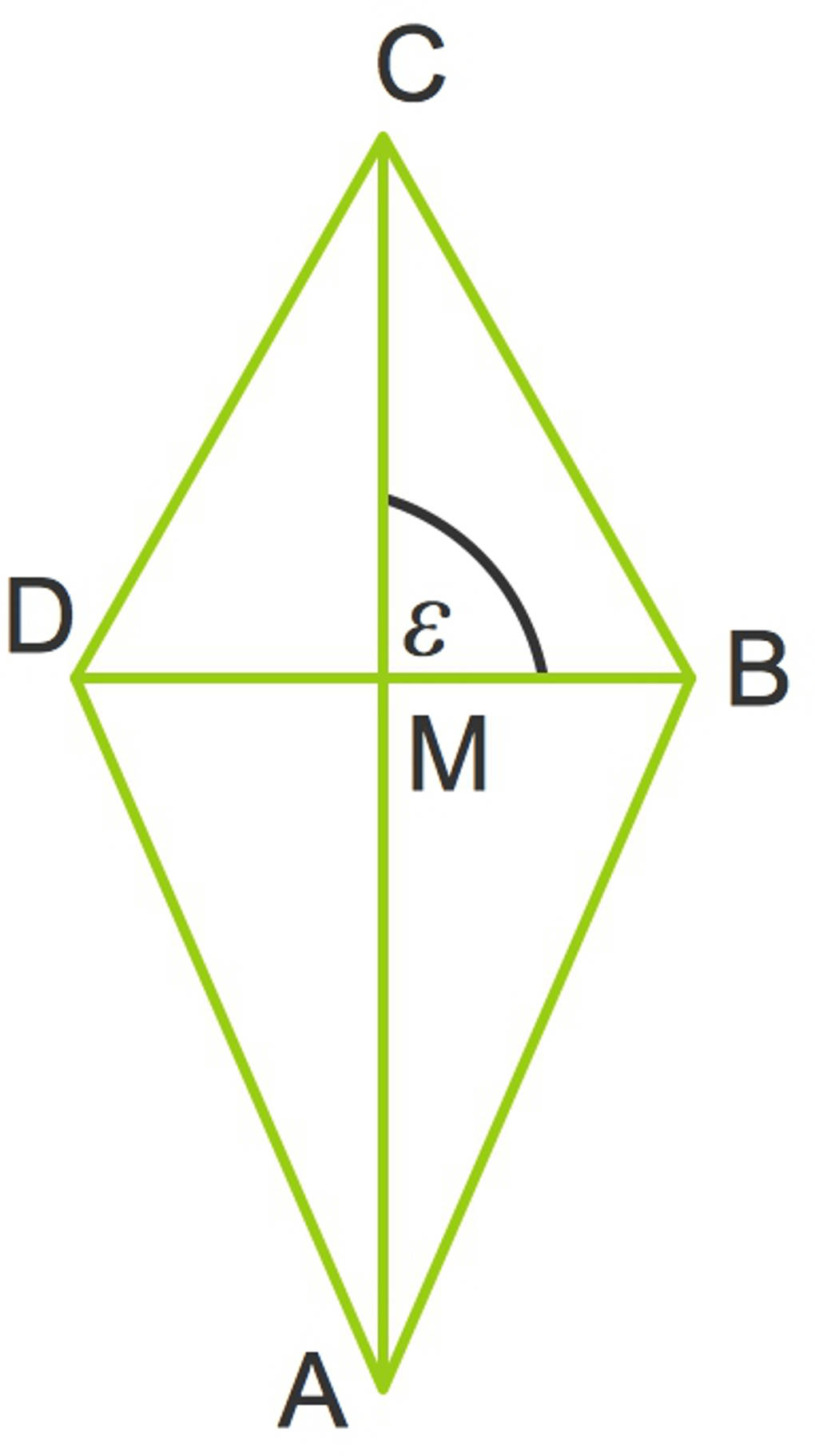
Die Dreiecke $ACD$ sowie $ABC$
- Die Strecken $\overline{AD}$ sowie $\overline{AB}$ sind gleich lang, da es sich um ein Drachenviereck handelt.
- Mit der gleichen Begründung stimmen auch die Strecken $\overline{BC}$ sowie $\overline{CD}$ überein.
- Die beiden Dreiecke haben die Strecke $\overline{AC}$ gemeinsam.
Das bedeutet, dass die beiden Dreiecke in ihren drei Seiten übereinstimmen und somit kongruent sind. Daraus kannst du schließen, dass die Winkel $\angle(ACD)$ sowie $\angle(ACB)$ gleich groß sind.
Die Dreiecke $CDM$ sowie $BCM$
- Die beiden Dreiecke haben die Strecke $\overline{CM}$ gemeinsam.
- Die Winkel $\angle(ACD)$ sowie $\angle(ACB)$ sind gleich groß.
- Die beiden Strecken $\overline{BC}$ sowie $\overline{CD}$ sind gleich lang.
Die beiden Dreiecke stimmen also in zwei Seiten und dem von diesen Seiten eingeschlossenen Winkel überein. Dies ist der Kongruenzsatz SWS. Sie sind demnach kongruent.
Daraus folgt, dass die beiden Winkel $\angle(CMD)$ sowie $\epsilon=\angle(CMB)$ gleich groß sind. Da die Summe dieser beiden Winkel gerade $180^\circ$ ist, folgt $2\epsilon=180^\circ$. Division durch $2$ führt zu $\epsilon=90^\circ$.
Die Diagonalen in einem Drachenviereck schneiden sich also in einem rechten Winkel.
Dies gilt übrigens auch für jedes Quadrat und für jede Raute.
Alle Videos zum Thema
Videos zum Thema
Seitenlängen, Diagonalen und Winkel in Vierecken (3 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Seitenlängen, Diagonalen und Winkel in Vierecken (2 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Primzahlen
- Geometrische Lagebeziehungen
- Rechteck
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Quadrat
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Was Ist Eine Viertelstunde
- Prisma
- Mitternachtsformel
- Grundrechenarten Begriffe
- Dreiecksarten
- Quader
- Satz Des Pythagoras
- Dreieck Grundschule
- Erste Binomische Formel
- Kreis
- Standardabweichung
- Flächeninhalt
- Volumen Kugel
- Zahlen In Worten Schreiben
- Meter
- Orthogonalität
- Schriftlich Multiplizieren
- Brüche Multiplizieren
- Potenzgesetze
- Distributivgesetz
- Flächeninhalt Dreieck
- Rationale Zahlen
- Volumen Berechnen
- Brüche Addieren
- Kongruenz
- Exponentialfunktion
- Scheitelpunktform
- Logarithmus
- Erwartungswert
- Skalarprodukt
- Primfaktorzerlegung
- Quadratische Ergänzung
- Zinseszins
- Geradengleichung Aus Zwei Punkten Bestimmen
- Sinusfunktion





 Haus der Vierecke – Einführung
Haus der Vierecke – Einführung
 Innenwinkel im Parallelogramm
Innenwinkel im Parallelogramm









