Determinante einer Matrix
Die Determinante hilft dir beim Lösen von Gleichungssystemen und der Berechnung des Flächeninhaltes eines Parallelogramms oder des Volumens eines Spats
Inhaltsverzeichnis zum Thema
- Was ist eine Matrix?
- Was ist eine Determinante?
- Berechnung der Determinante einer Matrix
- Anwendungen der Determinante
Was ist eine Matrix?
Eine quadratische Matrix, zum Beispiel $A$, mit $2$ (oder $3$) Zeilen und Spalten hat die folgende Gestalt. Eine $[2\times 2]$-Matrix
$A=\begin{pmatrix} a& b \\c&d \end{pmatrix}$
oder eine $[3\times 3]$-Matrix
$A=\begin{pmatrix} a&b&c \\ d&e&f\\ g&h&i \end{pmatrix}$
Natürlich kann eine quadratische Matrix auch $n$ Zeilen und Spalten haben. Allgemein wird eine quadratische Matrix als $[n\times n]$-Matrix bezeichnet.
Was ist eine Determinante?
- In der linearen Algebra ist die Determinante eine Funktion, die einer $[n\times n]$-Matrix ein Skalar, also eine Zahl, zuordnet.
- Die zwei gebräuchlichsten Darstellungen für die Determinante einer Matrix A sind $\quad$ det$(A)$ und $|A|$.
- Es gilt: det$(A) = |A|$.
- Mit Hilfe der Determinante kannst du Gleichungssysteme lösen, den Flächeninhalt eines Parallelogramms berechnen oder das Volumen eines Spats.
Berechnung der Determinante einer Matrix
Die Determinante einer $[2\times 2]$-Matrix
Es ist
det$\begin{pmatrix} a& b \\c&d \end{pmatrix}=\left|\begin{array}{cc} a&b\\c&d \end{array}\right|=a\cdot d-c\cdot b$.
Das bedeutet:
- Du multiplizierst die Elemente der Hauptdiagonalen, von oben links nach unten rechts, und
- subtrahierst davon das Produkt der Elemente der Nebendiagonalen, von unten links nach oben rechts.
Lass uns dies einmal an einem Beispiel üben.
$\left|\begin{array}{cc} 2&3\\4&-1 \end{array}\right|=2\cdot (-1)-4\cdot 3=-2-12=-14$
Übrigens ist die Determinante der Matrix $0$, wenn die eine Zeile ein Vielfaches der anderen ist. Hier ein Beispiel:
$\left|\begin{array}{cc} 2&4\\-1&-2 \end{array}\right|=2\cdot (-2)-(-1)\cdot 4=-4-(-4)=-4+4=0$
Die Sarrus-Regel
Zur Berechnung der Determinante einer $[3\times 3]$-Matrix verwendest du die Sarrus-Regel. Schaue dir hierfür die Matrix an und schreibe die ersten beiden Spalten noch einmal rechts neben die Ausgangs-Matrix:
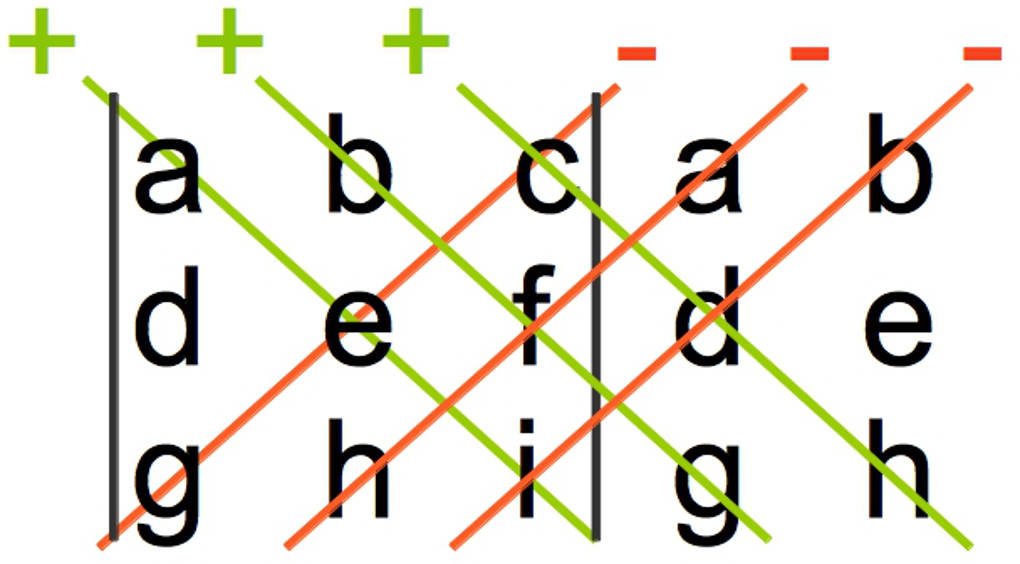
Hier ist angedeutet, dass du
- die Elemente von oben links nach unten rechts (grün) multiplizierst und die Produkte addierst und
- die Elemente von unten links nach oben rechts (rot) multiplizierst und die Produkte subtrahierst.
$\begin{array}{rcl}\left|\begin{array}{ccc} a& b&c \\d&e&f\\g&h&i \end{array}\right|&=&&a\cdot e\cdot i \color{#669900}{+}b\cdot f\cdot g\color{#669900}{+}c\cdot d\cdot h\\ &&\color{#669900}{-}&g\cdot e\cdot c\color{#669900}{-}h\cdot f\cdot a\color{#669900}{-}i\cdot d\cdot b \end{array}$
Auch diese Regel kannst du an einem Beispiel üben.
$\begin{array}{rcl}\left|\begin{array}{ccc} 3& -1&2 \\1&1&2\\2&1&-1 \end{array}\right|&=&~~3\cdot 1\cdot (-1)\color{#669900}{+}(-1)\cdot 2\cdot 2\color{#669900}{+}2\cdot 1\cdot 1\\ &&\color{#669900}{-}2\cdot 1\cdot 2\color{#669900}{-}1\cdot 2\cdot 3\color{#669900}{-}(-1)\cdot 1\cdot (-1)\\ &=&-3-4+2-4-6-1=-16 \end{array}$
Der Laplace'sche Entwicklungssatz
Ganz allgemein kann die Determinante einer $[n\times n]$-Matrix auch mit dem Laplace'schen Entwicklungssatz berechnet werden. Dabei wird die Determinante entweder spalten- oder zeilenweise ermittelt.
Zum Beispiel kannst du die Determinante der obigen $[3\times 3]$-Matrix auch mit der ersten Spalte entwickeln:
- Du multiplizierst das $(-1)^{i+1}$-fache des Elementes in der $i$-ten Zeile und ersten Spalte mit der Determinante der Untermatrix, welche entsteht, wenn du aus der Ausgangsmatrix die $i$-te Zeile und erste Spalte streichst.
- Dieses Produkt berechnest du für jedes Element in der ersten Spalte und
- addierst die Produkte.
$\begin{array}{rcl}\left|\begin{array}{ccc} 3& -1&2 \\1&1&2\\2&1&-1 \end{array}\right|&=&(-1)^{1+1}\cdot 3\cdot \left|\begin{array}{cc} 1&2\\1&-1 \end{array}\right|+(-1)^{2+1}\cdot 1 \cdot \left|\begin{array}{cc} -1&2\\1&-1 \end{array}\right|\\ &&+(-1)^{3+1}\cdot 2 \cdot \left|\begin{array}{cc} -1&2\\1&2 \end{array}\right|\\ &=&3\cdot(-1-2)-1\cdot (1-2)+2\cdot (-2-2)\\ &=&-9+1-8=-16 \end{array}$
Du erhältst natürlich die gleiche Determinante.
Anwendungen der Determinante
Die Cramer'sche Regel
Mit Hilfe der Cramer'schen Regel kannst du lineare Gleichungssysteme lösen. Dies ist hier am Beispiel eines Gleichungssystems mit zwei Gleichungen und zwei Unbekannten zu sehen.
$\begin{array}{rcrcl} 2x&-&3y&=&7\\ x&+&4y&=&-2 \end{array}$
$~~$
- Zuerst stellst du die Koeffizientenmatrix $A$ dieser Gleichung auf. Diese erhältst du, indem du die Koeffizienten der Unbekannten in einer $[2\times 2]$-Matrix aufschreibst. Von dieser Matrix berechnest du die Determinante.
$\quad~~~\text{det}(A)=\left|\begin{array}{cc} 2&-3\\ 1&4 \end{array}\right|=8-(-3)=11$
- Zur Berechnung der Lösung für $x$ ersetzt du in der Koeffizientenmatrix die entsprechende, also die erste, Spalte durch die rechte Seite der Gleichung und berechnest von der so erhaltenen Matrix $A_x$ wieder die Determinante.
$\quad~~~\text{det}(A_x)\left|\begin{array}{cc} 7&-3\\ -2&4 \end{array}\right|=28-6=22$
- Nun kannst du $x$ berechnen. Du dividierst die so berechneten Determinanten.
$\quad~~~x=\frac{\text{det}(A_x)}{\text{det}(A)}=\frac{22}{11}=2$
- Ebenso kannst du die Lösung für $y$ ermitteln. Dieses Mal ersetzt du in der Koeffizientenmatrix die zweite Spalte ($y$-Spalte) durch die rechte Seite der Gleichung und berechnest die Determinante.
$\quad~~~\text{det}(A_y)\left|\begin{array}{cc} 2&7\\ 1&-2 \end{array}\right|=-11$
- Somit ist
$\quad~~~y=\frac{\text{det}(A_y)}{\text{det}(A)}=\frac{-11}{11}=-1$.
Flächenberechnung eines Parallelogramms
Ein von den Vektoren $\vec a$ und $\vec b$ aus dem $\mathbb{R}^2$ aufgespanntes Parallelogramm kannst du hier sehen:
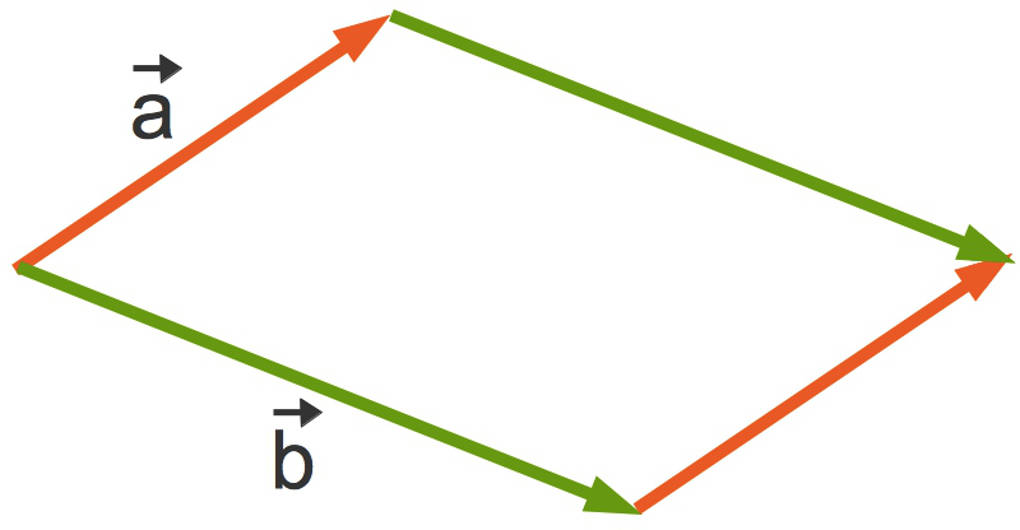
Den Flächeninhalt dieses Parallelogramms erhältst du, indem du die Determinante der Matrix berechnest, welche entsteht, wenn du die beiden Vektoren nebeneinander schreibst. Der Flächeninhalt ist dann der Betrag dieser Determinante.
Sei zum Beispiel
- $\vec a=\begin{pmatrix} 3 \\ 2 \end{pmatrix}$ sowie
- $\vec b=\begin{pmatrix} 5 \\ -2 \end{pmatrix}$.
Dann ist
$\left|\begin{array}{cc} 3&5\\ 2&-2 \end{array}\right|=-6-10=-16$
und somit $A_{\text{Parallelogramm}}=|-16|=16$ [FE].
Volumenberechnung eines Spats
Ein Spat oder auch Parallelepiped ist ein geometrischer Körper. Die begrenzenden Flächen sind paarweise kongruente, in parallelen Ebenen liegende Parallelogramme. Hier siehst du ein Spat.
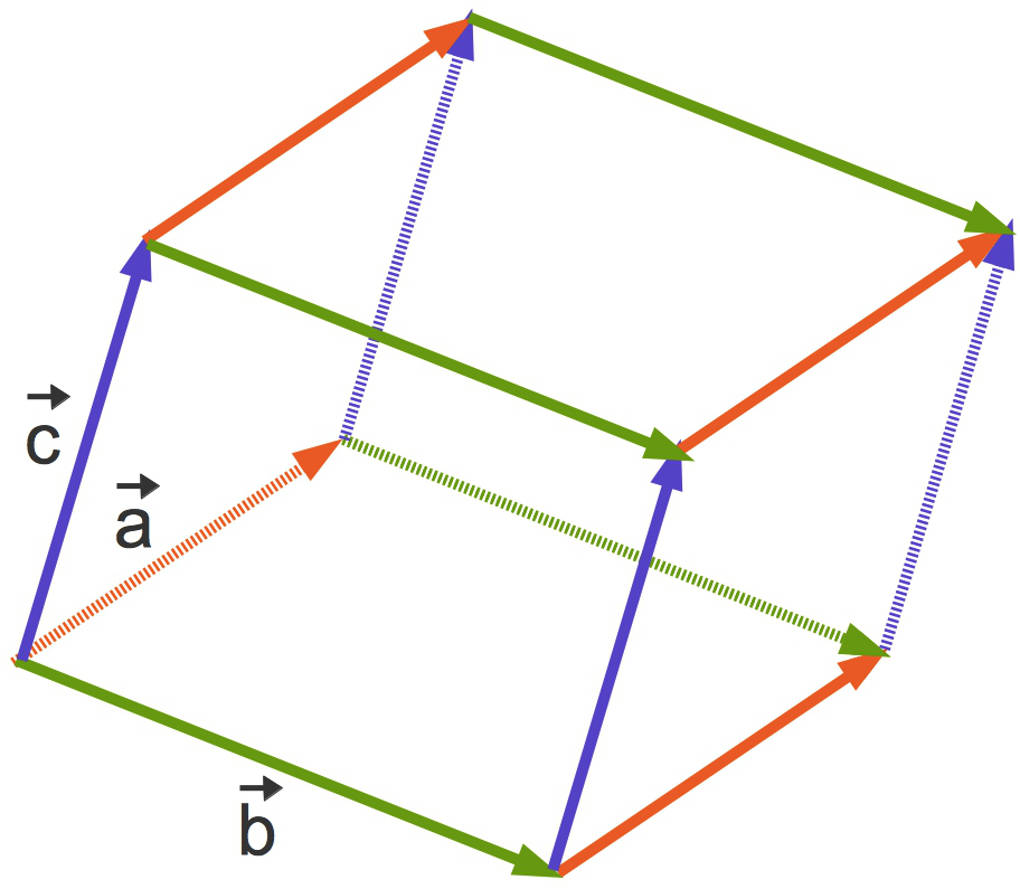
Dieses Spat wird von den drei Vektoren $\vec a$, $\vec b$ und $\vec c$ aus dem $\mathbb{R}^3$ aufgespannt.
Das Volumen eines solchen Spats ist gegeben durch das Spatprodukt:
$V_{\text{Spat}}=\left|\left(\vec a\times\vec b\right)\cdot \vec c\right|. $
Dieses Spatprodukt ist der Betrag der Determinante der $[3\times 3]$-Matrix, welche entsteht, wenn du die drei Vektoren $\vec a$, $\vec b$ und $\vec c$ nebeneinander schreibst.
Alle Videos zum Thema
Videos zum Thema
Determinante einer Matrix (4 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Determinante einer Matrix (4 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Primzahlen
- Geometrische Lagebeziehungen
- Rechteck
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Quadrat
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Was Ist Eine Viertelstunde
- Prisma
- Mitternachtsformel
- Grundrechenarten Begriffe
- Dreiecksarten
- Quader
- Satz Des Pythagoras
- Dreieck Grundschule
- Erste Binomische Formel
- Kreis
- Standardabweichung
- Flächeninhalt
- Volumen Kugel
- Zahlen In Worten Schreiben
- Meter
- Orthogonalität
- Schriftlich Multiplizieren
- Brüche Multiplizieren
- Potenzgesetze
- Distributivgesetz
- Flächeninhalt Dreieck
- Rationale Zahlen
- Volumen Berechnen
- Brüche Addieren
- Kongruenz
- Exponentialfunktion
- Scheitelpunktform
- Logarithmus
- Erwartungswert
- Skalarprodukt
- Primfaktorzerlegung
- Quadratische Ergänzung
- Zinseszins
- Geradengleichung Aus Zwei Punkten Bestimmen
- Sinusfunktion





 Determinante berechnen
Determinante berechnen
 Cramersche Regel
Cramersche Regel
 Cramersche Regel – Beispiele
Cramersche Regel – Beispiele
 Cramersche Regel – Beweis
Cramersche Regel – Beweis









