Gegenseitige Lage Ebene-Ebene
Spurgeraden, Schnittwinkel, Schnittgerade, Parallelität, Identität, Orthogonalität, Hessesche Normalform, Abstandsformel, Lotfußpunktverfahren, Normalenvektoren
Beliebteste Videos
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
Lagebeziehung von Ebenen
Wie zwei Ebenen zueinander liegen, kannst du am besten rechnerisch herausfinden. Die beiden Ebenen können dabei in drei verschiedenen Ebenengleichungen vorliegen, nämlich in der Parameterform, der Koordinatenform oder der Hesseschen Normalform.
Jede dieser Formen hat ihre Vorteile und Nachteile, je nachdem, was du damit berechnen möchtest. Für die nachfolgenden Berechnungen solltest du alle drei Formen gut kennen. Manchmal ist es auch notwendig, dass du von einer Form in die andere umrechnen musst, zum Beispiel von der Parameterform in die Koordinatenform.
Zwei Ebenen im Raum können auf drei verschiedene Weisen zueinander liegen. Sie können sich in einer Schnittgeraden schneiden, parallel zueinander oder identisch sein.

Ebenen schneiden sich
Du möchtest nun berechnen, ob und wie sich zwei Ebenen schneiden. Damit die Berechnung möglichst einfach wird, sollte eine der Ebenen in der Parameterform und die andere in der Koordinatenform vorliegen. Denn dann kannst du diese einfach ineinander einsetzen. Wir betrachten nun die Ebenen $E_1$ und $E_2$, deren Gleichungen wie folgt gegeben sind:
$ E_1: \vec x = \begin{pmatrix} 2\\ 1\\0\end{pmatrix} + r\cdot\begin{pmatrix} 1\\ -2\\-1\end{pmatrix} + s \cdot \begin{pmatrix} 4\\ 2\\-2\end{pmatrix} = \begin{pmatrix} 2+r+4s\\ 1-2r+2s\\-r-2s\end{pmatrix} $
$E_2: -3x_1 + 4x_2 – x_3 = 2$
Nun setzen wir die einzelnen Koordinaten von $E_1$ in $E_2$ ein:
$ \begin{array}{rcll} -3(2+r+4s) + 4(1-2r +2s)-(-r-2s) &=& 2&\\ -6-3r-12s+4-8r+8s+r+2s &=& 2&\\ -2-10r-2s &=& 2 &| +2\\ -10r-2s &=& 4 &| +10r\\ -2s &=& 4+10r &| :(-2)\\ s &=& -2-5r &\\ \end{array} $
Du erhältst eine Beziehung zwischen den zwei Parametern $r$ und $s$. Das bedeutet, dass sich die beiden Ebenen in einer Schnittgeraden schneiden. Nach welchem Parameter du dabei auflöst, kannst du frei wählen.
Die Gleichung der Schnittgeraden $g$ bekommst du, indem du in $E_1$ den Parameter $s$ durch den vorher berechneten Ausdruck $s=-2-5r$ ersetzt:
$ \begin{array}{rcl} g:\vec x &=& \begin{pmatrix} 2\\ 1\\0\end{pmatrix} + r\cdot\begin{pmatrix} 1\\ -2\\-1\end{pmatrix} + (-2-5r) \cdot \begin{pmatrix} 4\\ 2\\-2\end{pmatrix}\\ &=&\begin{pmatrix} 2\\ 1\\0\end{pmatrix} + r\cdot\begin{pmatrix} 1\\ -2\\-1\end{pmatrix} + \begin{pmatrix} -8-20r\\ -4-10r\\4+10r\end{pmatrix}\\ &=&\begin{pmatrix} 2\\ 1\\0\end{pmatrix} + r\cdot\begin{pmatrix} 1\\ -2\\-1\end{pmatrix} + \begin{pmatrix} -8\\ -4\\4\end{pmatrix} + r\cdot\begin{pmatrix} -20\\ -10\\10\end{pmatrix} \\ &=&\begin{pmatrix} -6\\ -3\\4\end{pmatrix} + r\cdot\begin{pmatrix} -19\\ -12\\9\end{pmatrix}\\ \end{array} $
Wenn sich zwei Ebenen schneiden, dann also in unendlich vielen Punkten. Diese Punkte liegen alle auf einer Geraden. Doch in welchem Winkel treffen die Ebenen dabei aufeinander?
Schnittwinkel berechnen
Den Schnittwinkel im Raum kannst du ganz einfach berechnen, sobald du die beiden Normalenvektoren der Ebenen kennst.
Bei der Normalenform ist der Normalenvektor direkt angegeben. Liegt die Ebenengleichung in der Koordinatenform vor, kannst du den Normalenvektor an den Koeffizienten ablesen. Mit Koeffizienten meint man die Zahlen, die vor den Variablen $x_1$, $x_2$ und $x_3$ stehen. Sieh dir dafür die folgenden Ebenen $E_3$ und $E_4$ an:
$\begin{array}{lllll} E_3: 2x_1 -x_2 = 2 && \Rightarrow && \vec n = \begin{pmatrix} 2\\ -1\\0\end{pmatrix}\\ E_4: 3x_3 -x_1+0,5x_2 = 5 && \Rightarrow && \vec n = \begin{pmatrix} -1\\ 0,5\\3\end{pmatrix} \end{array}$
Was ist aber, wenn die Ebenengleichung in der Parameterform gegeben ist? Auch hier musst du nicht verzweifeln! Denn der Normalenvektor einer Ebene steht jeweils orthogonal (senkrecht) auf den beiden Spannvektoren. Das heißt, das Skalarprodukt des Normalenvektors und einem Spannvektor ist $0$. Alternativ kannst du natürlich auch die Ebenengleichung in die Koordinatenform bringen und den Normalenvektor ablesen.
Wenn du nun die beiden Normalenvektoren $\vec m$ und $\vec n$ kennst, kannst du den Winkel wie folgt bestimmen:
$ \cos (\gamma) = \dfrac{|\vec m * \vec n|}{|\vec m|\cdot|\vec n|} $
Der Kosinus des eingeschlossenen Winkels $\gamma$ ist also gleich dem Betrag des Skalarprodukts der beiden Normalenvektoren geteilt durch das Produkt der Längen der Normalenvektoren.
Ebenen schneiden Koordinatenebenen
Zwei Ebenen können sich also aufgrund ihrer gegenseitigen Lage schneiden und man kann die Schnittgerade sowie den Schnittwinkel im Raum berechnen. Die Schnittgeraden einer Ebene mit den Koordinatenebenen sind dabei eine Besonderheit. Diese werden auch Spurgeraden genannt. Bei der Berechnung der Spurgeraden kannst du genauso vorgehen wie bei der obigen Berechnung der Schnittgeraden zweier Ebenen.
Ebenen sind identisch
Es gibt sogar Ebenen, die sich nicht nur in einer Schnittgeraden schneiden, sondern in allen Punkten. Die Ebenen sind dann identisch. Trotzdem kannst du das oft nicht auf einen Blick erkennen. Vor allem, wenn die beiden Ebenen in unterschiedlichen Formen gegeben sind.
Setzt du zwei identische Ebenen ineinander ein wie oben, erhältst du einen wahren Ausdruck. Das heißt, z.B. $5=5$ oder auch $0=0$.
Ebenen sind echt parallel
Erhältst du hingegen beim ineinander Einsetzen einen falschen Ausdruck wie $4=5$, sind die Ebenen parallel zueinander. Sie schneiden sich also in keinem Punkt. Wenn zwei Ebenen parallel sind, kannst du deren Abstand zueinander bestimmen.
Abstand zwischen zwei Ebenen
Den Abstand $r$ zwischen zwei Ebenen kannst du z.B. mit der Abstandsformel berechnen. Dafür benötigst du eine Ebene in der Hesseschen Normalform:
$ \dfrac{n_x\cdot x + n_y\cdot y + n_z \cdot z -d}{\sqrt{{n_x}^2+{n_y}^2+{n_z}^2}}=0 $
Zudem benötigst du einen beliebigen Punkt $Q$ der anderen Ebene (z.B. den Stützvektor). Die Abstandsformel lautet dann:
$ r =\Biggl|\dfrac{n_x\cdot x_Q + n_y\cdot y_Q + n_z\cdot z_Q -d}{\sqrt{{n_x}^2+{n_y}^2+{n_z}^2}}\Biggl| $
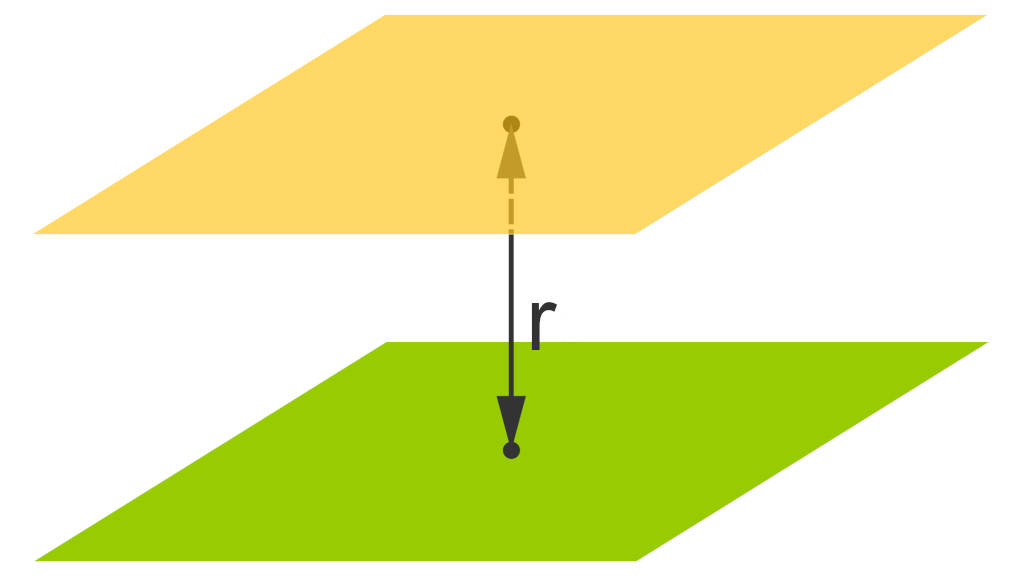
Alternativ dazu kannst du auch das Lotfußpunktverfahren anwenden. Dabei stellst du eine Hilfsgerade auf. Als Stützvektor wählst du den Ortsvektor eines beliebigen Punkts $Q$ der ersten Ebene. Als Richtungsvektor nimmst du einen der beiden Normalenvektoren.
Diese Hilfsgerade schneidet die zweite Ebene in einem Lotfußpunkt $L$. Die Länge des Vektors $\vec{QL}$ ist dann der Abstand zwischen den Ebenen.
Alle Videos zum Thema
Videos zum Thema
Gegenseitige Lage Ebene-Ebene (3 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Gegenseitige Lage Ebene-Ebene (3 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Primzahlen
- Geometrische Lagebeziehungen
- Rechteck
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Quadrat
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Was Ist Eine Viertelstunde
- Prisma
- Mitternachtsformel
- Grundrechenarten Begriffe
- Dreiecksarten
- Quader
- Satz Des Pythagoras
- Dreieck Grundschule
- Erste Binomische Formel
- Kreis
- Standardabweichung
- Flächeninhalt
- Volumen Kugel
- Zahlen In Worten Schreiben
- Meter
- Orthogonalität
- Schriftlich Multiplizieren
- Brüche Multiplizieren
- Potenzgesetze
- Distributivgesetz
- Flächeninhalt Dreieck
- Rationale Zahlen
- Volumen Berechnen
- Brüche Addieren
- Kongruenz
- Exponentialfunktion
- Scheitelpunktform
- Logarithmus
- Erwartungswert
- Skalarprodukt
- Primfaktorzerlegung
- Quadratische Ergänzung
- Zinseszins
- Geradengleichung Aus Zwei Punkten Bestimmen
- Sinusfunktion








 Gegenseitige Lage Ebene-Ebene
Gegenseitige Lage Ebene-Ebene
 Gegenseitige Lage Ebene-Ebene – Beispiele
Gegenseitige Lage Ebene-Ebene – Beispiele
 Schnittwinkel im Raum
Schnittwinkel im Raum









