Integralrechnung – Anwendungsaufgaben
Anwendungsgebiete der Integralrechnung sind Flächenberechnung, Rekonstruktion von Beständen, Berechnung von Kräften und Bewegungen.
Beliebteste Videos
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Das unbestimmte und das bestimmte Integral
- Flächenberechnung
- Federkraft
- Berechnung einer Bogenlänge
- Rekonstruktion von Beständen
Das unbestimmte und das bestimmte Integral
Das unbestimmte Integral
Gegeben sei $f$, eine beliebige reelle und integrierbare Funktion. Jede differenzierbare Funktion $F$, deren Ableitung $F'=f$ ist, wird Stammfunktion der Funktion $f$ genannt.
Sei $F$ eine Stammfunktion von $f$, also $F'(x)=f(x)$, dann gilt auch, dass $F_{C}(x)=F(x)+C$ mit einer Konstanten $C\in\mathbb{R}$ eine Stammfunktion von $f(x)$ ist. $C$ wird Integrationskonstante genannt.
Die Menge aller Stammfunktionen einer Funktion $f$ ist das unbestimmte Integral von $f$, also
$\int~f(x)~dx = \{ F(x) | F'(x)=f(x) \}$
Das bestimmte Integral
Bei einem bestimmten Integral kommen noch Integrationsgrenzen $a$ und $b$ hinzu:
$\int\limits_a^b~f(x)~dx $
Hierbei ist $a$ die untere und $b$ die obere Integrationsgrenze.
Der Hauptsatz der Differential- und Integralrechnung
Das bestimmte Integral kannst du mit Hilfe des Hauptsatzes der Differential- und Integralrechnung berechnen:
$\int\limits_a^b~f(x)~dx =\left[F(x)\right]_a^b=F(b)-F(a)$
Dabei ist $F$ eine Stammfunktion von $f$.
Flächenberechnung
Der Funktionsgraph von $f$ mit $f(x)=x^2+3$ schließt mit der $x$-Achse über dem Intervall $[1;2]$ ein Flächenstück ein. Berechne den Inhalt dieser Fläche. Diese ist in dem Bild schraffiert.
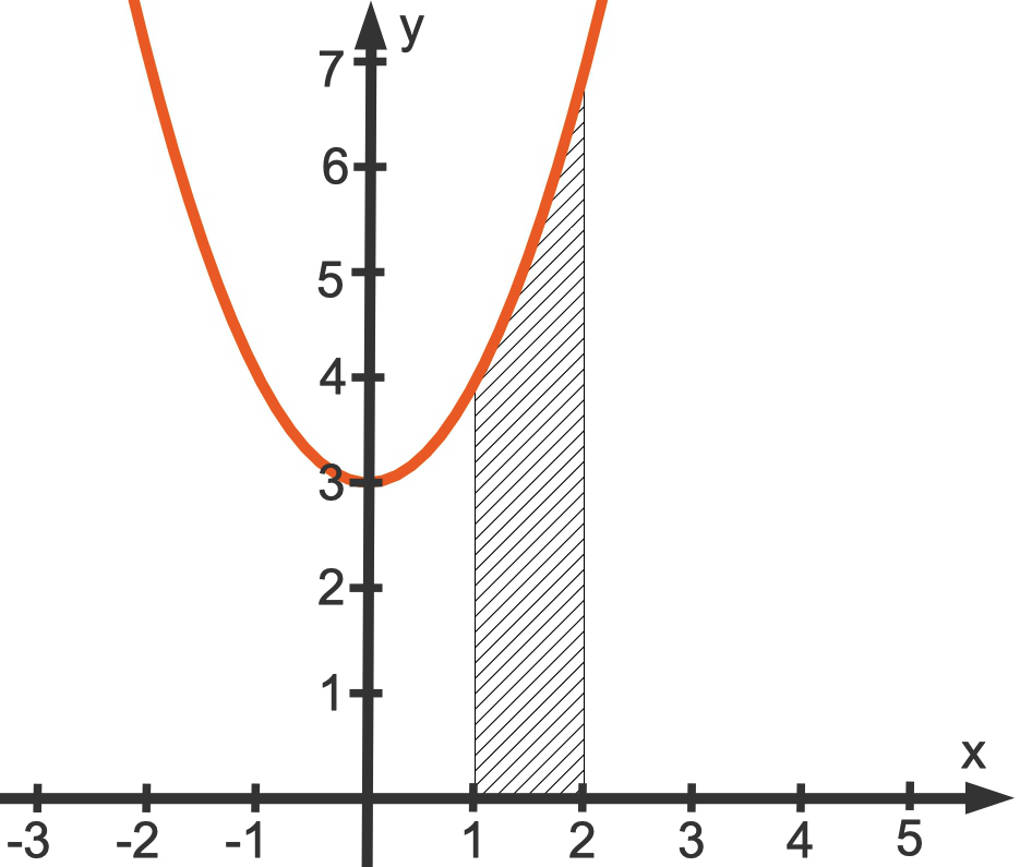
Da der Funktionsgraph über dem betrachteten Intervall komplett oberhalb der $x$-Achse liegt, ist der Flächeninhalt gegeben durch $A=\int\limits_1^2~(x^2+3)~dx$.
- Bestimme zunächst eine Stammfunktion $F$ von $f$. Hierfür verwendest du die Potenzregel sowie die Summenregel der Integration: $F(x)=\frac13x^3+3x$.
- Wende nun den Hauptsatz der Differential- und Integralrechnung an:
$\begin{array}{rcl} A&=&\int\limits_1^2~(x^2+3)~dx\\ &=&\left[\frac13x^3+3x\right]^2_1\\ &=&\left(\frac13\cdot 2^3+3\cdot 2\right)-\left(\frac13\cdot1^3+3\cdot 1\right)\\ &=&\frac{16}3~\text{[FE]}\end{array}$
Federkraft
Wenn du eine Feder zusammendrücken möchtest, wirkt diese mit der Kraft $F$, der Federkraft, der von dir aufgebrachten Kraft entgegen. Diese Federkraft ist proportional zur zusammengestauchten Strecke $s$. Verwende nach dem Hookeschen Gesetz die folgende Formel: $F(s)=D\cdot s$ mit der Federkonstanten $D=10~\frac{\text{N}}{\text{cm}}$.
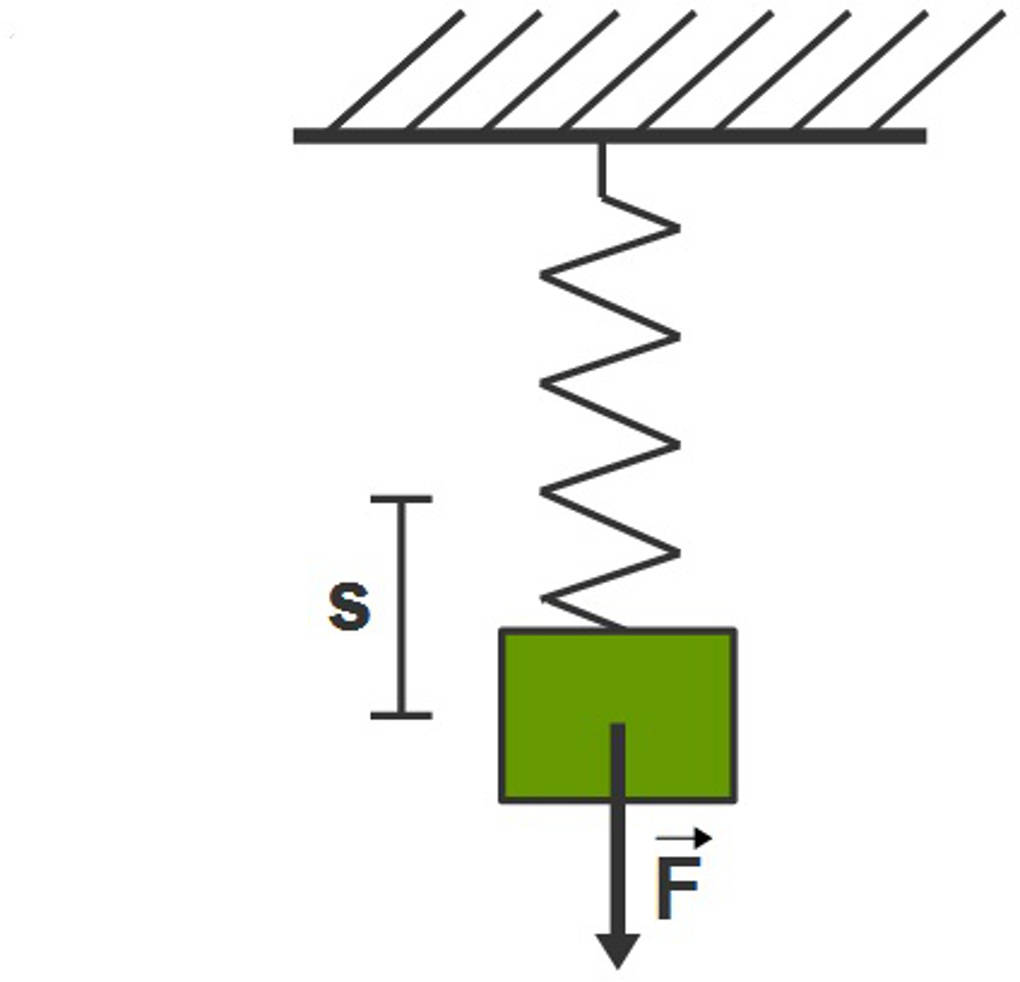
Die Arbeit, welche du aufbringen musst, um die Feder um $s=20~\text{cm}$ zusammenzudrücken, beträgt
$\Delta W=\int\limits_0^{20}~F(s)~ds=\left[\frac12 \cdot D\cdot s^2\right]_0^{20}=2000~\text{[N]}$.
Berechnung einer Bogenlänge
Mit Hilfe der Integration kannst du die Länge eines Bogens bestimmen. Wir schauen uns nochmal das obige Beispiel der quadratischen Funktion $f$ mit $f(x)=x^2+3$ an. Wie lang ist der Bogen des Funktionsgraphen über dem Intervall $[1;2]$?
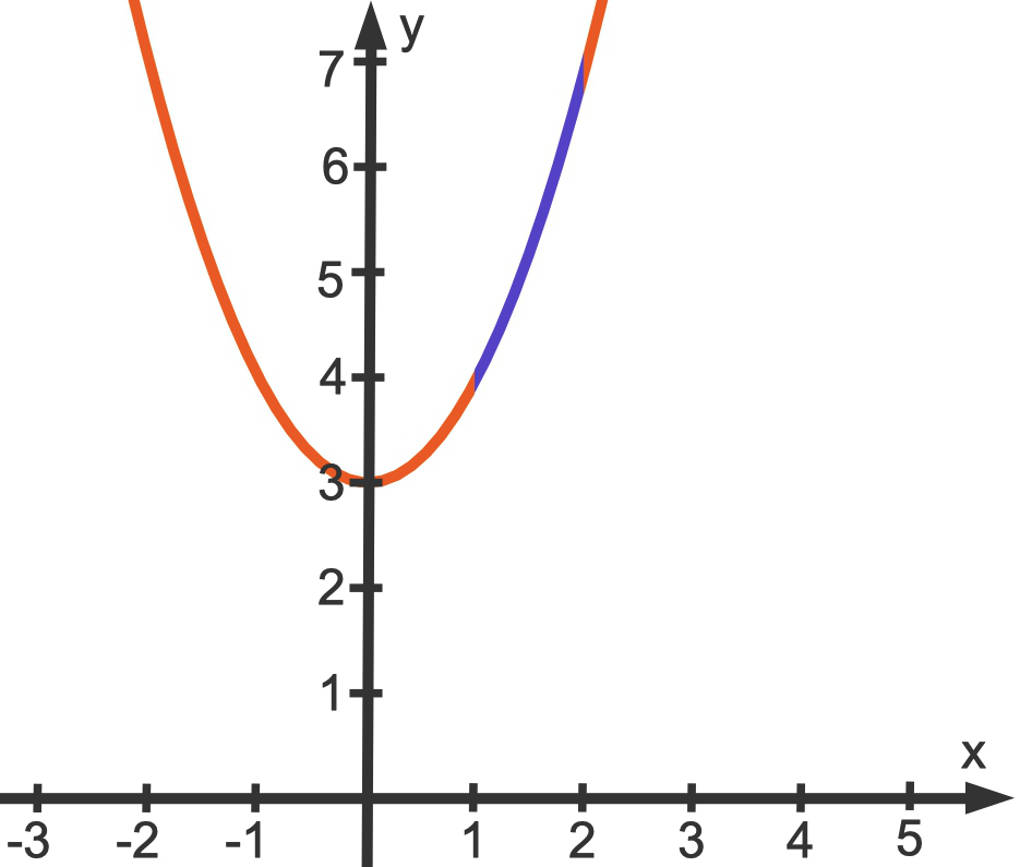
Diese kannst du mit der folgenden Formel berechnen. Dabei sind die Integrationsgrenzen die entsprechenden Intervallgrenzen.
$L=\int\limits_a^b~\sqrt{1+(f'(x))^2}~dx$
Nun kannst du starten:
$L=\int\limits_1^2~\sqrt{1+(2x)^2}~dx=\int\limits_1^2~\sqrt{1+4x^2}~dx\approx 3,17~[\text{LE}]$
Rekonstruktion von Beständen
Eine weitere Anwendung der Integration ist die Rekonstruktion von Beständen. Wir schauen uns ein Beispiel zum freien Fall an.
Wenn ein Gegenstand aus einer Höhe von $50$ Metern fallen gelassen wird, bewegt er sich mit der Geschwindigkeit $v$ mit $v(t)=g\cdot t$ mit $g\approx 9,81~\frac{\text{m}}{\text{s}^{2}}$.
Mit Hilfe der Potenzregel der Integration erhältst du als eine Stammfunktion $s$ zu $v$ die Funktion $s(t)=\frac12\cdot g\cdot t^{2}$. Die Größe $s(t)$ steht dabei für den zurückgelegten Weg in Metern pro $t$ Sekunden. Im Folgenden gilt $s(0)=0$. Das bedeutet, dass zum Zeitpunkt $0$ Sekunden noch kein Weg zurückgelegt wurde. Du kommst damit zu $s$ mit $s(t)=4,905\cdot t^{2}$.
- Du kannst nun bestimmen, wie tief der Gegenstand nach drei Sekunden gefallen ist $s(3)=44,145$. Der Gegenstand ist also ungefähr $44$ Meter gefallen.
- Wann kommt der Gegenstand auf dem Boden auf? Löse hierfür die Gleichung $4,905\cdot t^{2}=50$. So erhältst du $t\approx 3,2$. Nach etwa $3,2$ Sekunden kommt der Gegenstand auf dem Boden auf.
Alle Videos zum Thema
Videos zum Thema
Integralrechnung – Anwendungsaufgaben (2 Videos)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Primzahlen
- Geometrische Lagebeziehungen
- Rechteck
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Quadrat
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Was Ist Eine Viertelstunde
- Prisma
- Mitternachtsformel
- Grundrechenarten Begriffe
- Dreiecksarten
- Quader
- Satz Des Pythagoras
- Dreieck Grundschule
- Erste Binomische Formel
- Kreis
- Standardabweichung
- Flächeninhalt
- Volumen Kugel
- Zahlen In Worten Schreiben
- Meter
- Orthogonalität
- Schriftlich Multiplizieren
- Brüche Multiplizieren
- Potenzgesetze
- Distributivgesetz
- Flächeninhalt Dreieck
- Rationale Zahlen
- Volumen Berechnen
- Brüche Addieren
- Kongruenz
- Exponentialfunktion
- Scheitelpunktform
- Logarithmus
- Erwartungswert
- Skalarprodukt
- Primfaktorzerlegung
- Quadratische Ergänzung
- Zinseszins
- Geradengleichung Aus Zwei Punkten Bestimmen
- Sinusfunktion














