Brüche ordnen und vergleichen
gemeiner Bruch, gemischter Bruch, umrechnen, Zahlenstrahl, ordnen
Beliebteste Videos
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Was ist ein Bruch?
- Vergleichen und Ordnen von Brüchen mit gemeinsamem Nenner
- Vergleichen und Ordnen von Brüchen mit verschiedenen Nennern
- Die Streifenmethode
Was ist ein Bruch?
Was Brüche sind, kannst du dir am besten an einem Beispiel klarmachen. Anne, Marie und Paul haben eine Pizza bestellt.
Diese teilen sie in drei gleich große Stücke. Jedes Stück ist ein Drittel der gesamten Pizza. Dies wird so geschrieben:

Du siehst: Da steht oben eine Zahl, dann ein Strich und unter dem Strich wieder eine Zahl.
- Der Strich ist der Bruchstrich. Er steht für das Divisionszeichen.
- Die Zahl unter dem Bruchstrich ist der Nenner. Sie benennt den Bruch, hier zum Beispiel „Drittel“. Der Nenner gibt also an, in wie viele Teile ein Ganzes geteilt wurde.
- Die Zahl über dem Bruchstrich ist der Zähler. Sie gibt an, wie viele Teile des Ganzes jeder der Freunde bekommt.
Vergleichen und Ordnen von Brüchen mit gemeinsamem Nenner
Du kannst dir den Nenner eines Bruches vorstellen wie eine Maßeinheit. Betrachten wir ein Beispiel:
Marie und Paul vergleichen die Längen ihrer Schulwege. Marie geht jeden Morgen $800~m$ zur Schule und Paul $1300~m$. Du erkennst sofort, dass Pauls Schulweg länger ist.
Ein wenig anders sieht das aus, wenn die Entfernung in verschiedenen Maßeinheiten gegeben sind: Die Entfernung von Maries Zuhause zur Schule beträgt $800~m$ und die von Pauls Zuhause $1,3~km$. Hier musst du zunächst in eine gemeinsame Maßeinheit, zum Beispiel Meter, umrechnen.
Doch wie funktioniert der Größenvergleich bei Brüchen? Ähnlich wie beim Vergleich von Längen, solltest du zunächst in eine gemeinsame "Maßeinheit" umrechnen. Schauen wir uns ein Beispiel an:
Du möchtest entscheiden, welcher Bruch der kleinste ist, der nächst kleinere und so weiter. Mathematisch schreibst du dies mit einem Verhältniszeichen, auch Relationszeichen genannt:
- $<$ für „kleiner als“ oder
- $>$ für „größer als“.
Haben Brüche denselben Nenner, so bezeichnet man sie als gleichnamig. Sind die Brüche gleichnamig, so musst du nur die Zähler vergleichen.
Das kannst du gleich mal üben. Hier sind verschiedene Brüche mit dem Nenner $10$.
$\frac{3}{10}$; $\frac{7}{10}$; $\frac{4}{10}$
Schau dir die Zähler an: $3<4<7$. So erhältst du die Anordnung für die Brüche:
$\frac{3}{10}~<~\frac{4}{10}~<~\frac{7}{10}$
Dies entspricht dem Beispiel mit den Entfernungen in Metern. Was kannst du tun, wenn die Brüche keinen gemeinsamen Nenner haben?
Vergleichen und Ordnen von Brüchen mit verschiedenen Nennern
Wenn die Brüche nicht gleichnamig sind, kannst du sie nicht vergleichen, indem du die Zähler vergleichst.
Schau dir nochmal das Beispiel mit der Pizza an. Maries Stück ist die Hälfte der Pizza und Pauls Stück ein Drittel. Welches der beiden Stücke ist größer?
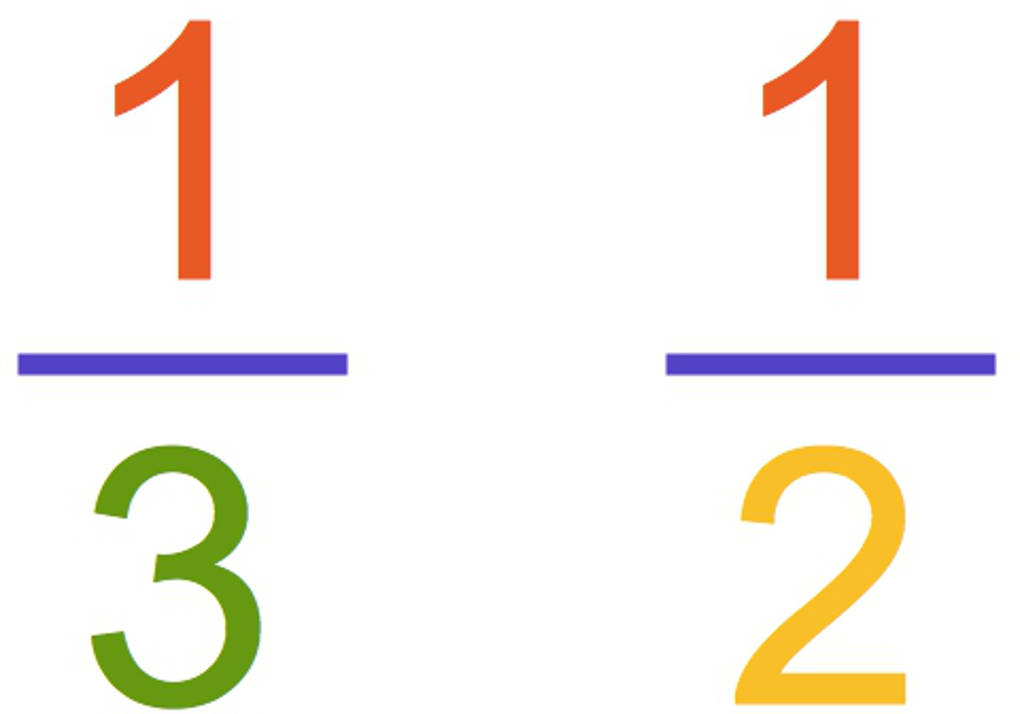
Welches Relationszeichen gehört hier hin?
Wie bei dem Beispiel mit den Entfernungen suchst du eine gemeinsame Maßeinheit. Die gemeinsame Maßeinheit bei Brüchen ist der gemeinsame Nenner.
Du erweiterst oder kürzt einen oder beide Brüche so, dass beide Brüche danach einen gemeinsamen Nenner haben.
Brüche erweitern
Brüche erweitern kannst du, indem du sowohl den Zähler als auch den Nenner mit derselben Zahl multiplizierst. Der Wert des Bruches bleibt dabei erhalten. Hier siehst du ein Beispiel:
$\frac13=\frac{1\cdot 2}{3\cdot 2}=\frac26$
Brüche kürzen
Indem du sowohl den Zähler als auch denn Nenner durch einen gemeinsamen Faktor dividierst (teilst), kannst du Brüche kürzen. Auch hier bleibt der Wert des Bruches erhalten. Schau dir das Beispiel an:
$\frac{10}{15}=\frac{10:5}{15:5}=\frac23$
Wie findest du den (kleinsten!) gemeinsamen Nenner?
Schau dir die Malfolgen der beiden Nenner an:
- Die Malfolge von $2$ ist $2$; $4$, $\color{#669900}{6}$; $8$; ...
- Die Malfolge von $3$ ist $3$; $\color{#669900}{6}$; 9;....
- Du siehst: die $6$ kommt in beiden Malfolgen vor.
- $6$ ist also ein Vielfaches von $2$ und $3$.
Um die beiden Brüche
$\frac13$ sowie $\frac12$
zu vergleichen, erweiterst du diese zunächst, um den gemeinsamen Nenner $6$ zu erhalten:
$\frac13=\frac{1\cdot 2}{3\cdot 2}=\frac26$
und
$\frac12=\frac{1\cdot 3}{2\cdot 3}=\frac36$
Nun sind die Brüche gleichnamig und du kannst die Zähler vergleichen. Da $2<3$ ist, erhältst du
$\frac13=\frac26<\frac36=\frac12$
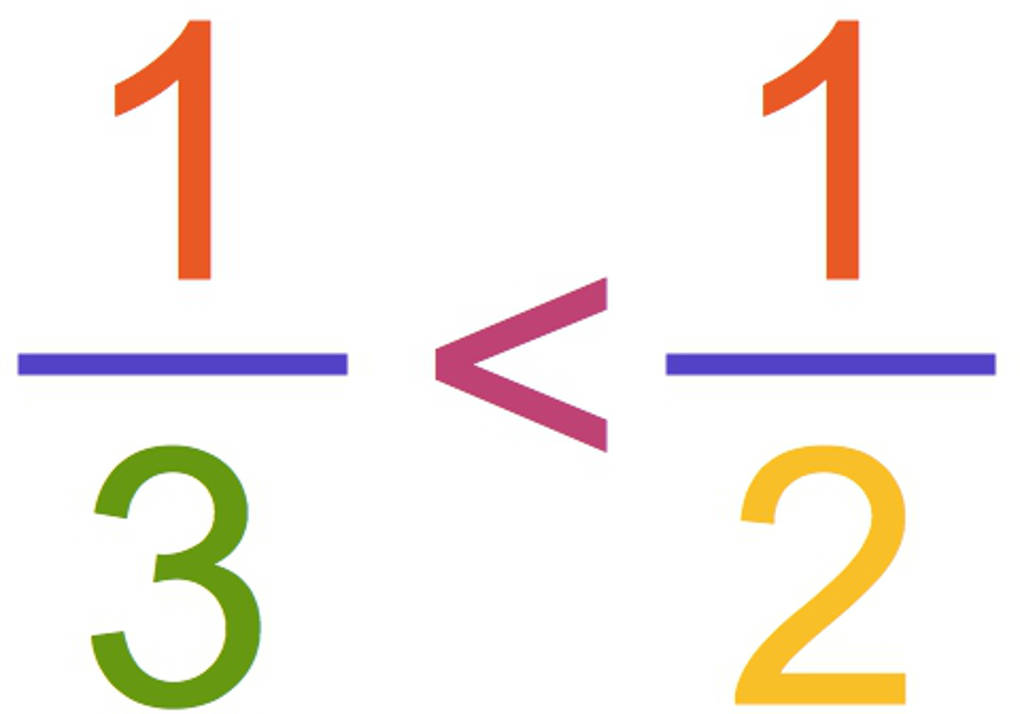
Pauls Pizzastück ist also kleiner als das von Marie.
Die Streifenmethode
Bei der Pizza hättest du dir dies sehr schön klarmachen können, indem du die Stücke direkt vergleichst.
Der Größenvergleich von Brüchen durch Bruchstreifen ist eine andere Möglichkeit Brüche zu vergleichen. Hierfür kannst du Brüche in Form von Bruchstreifen darstellen. Dies siehst du hier für das obige Beispiel.
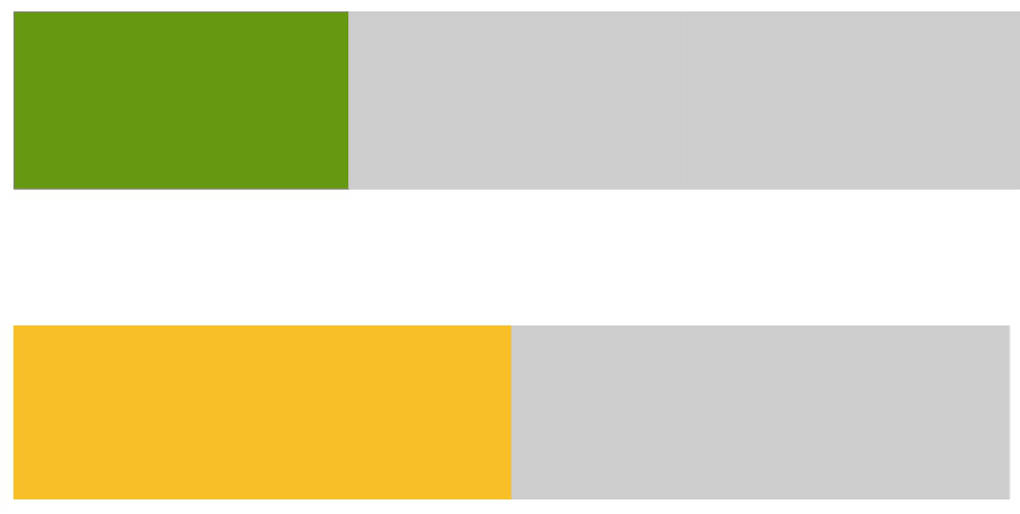
In dem oberen Bruchstreifen erkennst du, grün, ein Drittel $\left(\frac{1}{3}\right)$ und in dem unteren, orange, eine Hälfte $\left(\frac{1}{2}\right)$. Der grüne Streifen ist kleiner als der orangefarbene.
Alle Videos zum Thema
Videos zum Thema
Brüche ordnen und vergleichen (9 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Brüche ordnen und vergleichen (8 Arbeitsblätter)
-
 Brüche vergleichen
PDF anzeigen
Brüche vergleichen
PDF anzeigen -
 Gemeine Brüche in gemischte Brüche umwandeln
PDF anzeigen
Gemeine Brüche in gemischte Brüche umwandeln
PDF anzeigen -
 Brüche auf dem Zahlenstrahl
PDF anzeigen
Brüche auf dem Zahlenstrahl
PDF anzeigen -
 Brüche auf dem Zahlenstrahl – Übung
PDF anzeigen
Brüche auf dem Zahlenstrahl – Übung
PDF anzeigen -
 Brüche und Dezimalzahlen ordnen
PDF anzeigen
Brüche und Dezimalzahlen ordnen
PDF anzeigen -
 Größenvergleich bei Brüchen – Rechteckstreifen (1)
PDF anzeigen
Größenvergleich bei Brüchen – Rechteckstreifen (1)
PDF anzeigen -
 Größenvergleich bei Brüchen – Kürzen und Erweitern (2)
PDF anzeigen
Größenvergleich bei Brüchen – Kürzen und Erweitern (2)
PDF anzeigen -
 Größenvergleich bei Brüchen – Übung
PDF anzeigen
Größenvergleich bei Brüchen – Übung
PDF anzeigen
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Primzahlen
- Geometrische Lagebeziehungen
- Rechteck
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Quadrat
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Was Ist Eine Viertelstunde
- Prisma
- Mitternachtsformel
- Grundrechenarten Begriffe
- Dreiecksarten
- Quader
- Satz Des Pythagoras
- Dreieck Grundschule
- Erste Binomische Formel
- Kreis
- Standardabweichung
- Flächeninhalt
- Volumen Kugel
- Zahlen In Worten Schreiben
- Meter
- Orthogonalität
- Schriftlich Multiplizieren
- Brüche Multiplizieren
- Potenzgesetze
- Distributivgesetz
- Flächeninhalt Dreieck
- Rationale Zahlen
- Volumen Berechnen
- Brüche Addieren
- Kongruenz
- Exponentialfunktion
- Scheitelpunktform
- Logarithmus
- Erwartungswert
- Skalarprodukt
- Primfaktorzerlegung
- Quadratische Ergänzung
- Zinseszins
- Geradengleichung Aus Zwei Punkten Bestimmen
- Sinusfunktion






















