Gleichungen 3. Grades lösen – Polynomdivision

in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
Grundlagen zum Thema Gleichungen 3. Grades lösen – Polynomdivision
Was ist eine kubische Gleichung?
Du hast in Mathe bestimmt schon lineare Gleichungen, also Geradengleichungen kennengelernt. Und du kennst bestimmt auch schon quadratische Gleichungen, die man mit
$ax^{3}+bx^{2}+cx+d=0$
Man nennt diese Formel die allgemeine Form der kubischen Gleichung. Das Adjektiv kubisch bedeutet, dass die höchste Potenz der Variablen in der Gleichung $3$ ist und dass der Koeffizient $a$ dieser Potenz nicht null ist.
In diesem Video erklären wir dir, wie man kubische Gleichungen mithilfe der Polynomdivision auf quadratische Gleichungen reduzieren kann. Mit dieser Methode kannst du kubische Gleichungen mit Absolutglied lösen – also solche Gleichungen, bei denen der konstante Term $d$ in der allgemeinen Form nicht null ist.
Kubische Gleichungen – Definition
Eine kubische Gleichung ist eine Gleichung, in der die Variable $x$ bis zur dritten Potenz vorkommt. Der Koeffizient der dritten Potenz ist nicht null. In der allgemeinen Form der Gleichung:
$ax^{3}+bx^{2}+cx+d=0$
heißt der Term $ax^{3}$ kubischer Term, denn hier tritt die Variable $x$ zur dritten Potenz auf. Der Term $bx^{2}$ ist der quadratische Term, $cx$ der lineare Term und $d$ das Absolutglied. Das Absolutglied wird auch konstantes Glied genannt. In einer kubischen Gleichung kann auch einer oder mehrere der Terme $bx^{2}$ oder $bx$ oder $d$ fehlen. Fehlt aber der Term $ax^{3}$, so ist es keine kubische Gleichung mehr.
Lösungen polynomialer Gleichungen
Wir suchen in Mathe in der Regel nach reellen Lösungen polynomialer Gleichungen. Gesucht ist also ein Wert $x \in \mathbb R$, der nach Einsetzen in die Gleichung eine richtige Aussage ergibt. Die maximale Anzahl verschiedener Lösungen einer polynomialen Gleichung ist dasselbe wie der Grad der Gleichung: Eine lineare Gleichung
Entsprechend hat eine Gleichung dritten Grades
Kubische Gleichungen lösen mittels Polynomdivision
Nach dem Fundamentalsatz der Algebra lässt sich jedes kubische Polynom zerlegen in einen
$ax^{3}+bx^{2}+cx+d = (x-x_1) \cdot (rx^{2}+sx+t)$
Setzt du diese Terme gleich null, so kannst du den Satz vom Nullprodukt anwenden: Ein Produkt ist null genau dann, wenn mindestens einer seiner Faktoren null ist. Anders gesagt: Das Produkt $ax^{3}+bx^{2}+cx+d$ ist null genau dann, wenn der Faktor $(x-x_1)$ null ist oder wenn der Faktor $rx^{2}+sx+t$ null ist. So erhältst du aus der kubischen Gleichung $ax^{3}+bx^{2}+cx+d=0$ die lineare Gleichung $x-x_1=0$ und die quadratische Gleichung $rx^{2}+sx+d=0$. Man sagt auch: Du hast die kubische Gleichung auf eine lineare und eine quadratische Gleichung reduziert.
Ziel der Polynomdivision ist es, die Zerlegung der kubischen Gleichung zu bestimmen. Dazu suchen wir den geeigneten Linearfaktor $(x-x_1)$ und dividieren das Polynom $ax^{3}+bx^{2}+cx+d$ durch diesen Linearfaktor.
Wie findest du den passenden Linearfaktor? Die rechte Seite der
Kubische Gleichung lösen mit Polynomdivision – Beispiel
Wir lösen gemeinsam die kubische Gleichung $x^{3}-2x^{2}-5x+6=0$. Als Erstes suchen wir also eine Nullstelle $x_1$ der Funktion $f(x) = x^{3}-2x^{2}-5x+6$. Wir notieren von dem Absolutglied $d=6$ alle Teiler und ihre Negativen: $-6,-3,-2,-1,1,2,3,6$. Jeden dieser Werte können wir für $x$ einsetzen und probieren, ob die Gleichung erfüllt ist. Wir haben Glück: Für $x=1$ ergibt sich:
$f(1) = 1^{3}-2\cdot 1^{2}-5 \cdot 1^{1}+6 = 1-2-5+6=0$
Daher ist $x_{1}=1$ eine Nullstelle der Funktion $f$.
Als Nächstes führen wir die Polynomdivision durch: Wir dividieren das Polynom
Im ersten Schritt dividieren wir das höchste Glied $x^{3}$ durch das höchste Glied $x$ des Linearfaktors. Um die Division $x^{3}:x$ zu lösen, können wir auch fragen: Womit müssen wir $x$ multiplizieren, um $x^{3}$ zu erhalten? Mit $x^{2}$. Also
Im nächsten Schritt multiplizieren wir wie bei einer schriftlichen Division mit Zahlen diesen Term $x^{2}$ mit dem Divisor $(x-1)$ und schreiben das Ergebnis $(x-1)\cdot x^{2} = x^{3}-x^{2}$ ganz links unter den Dividenden:
Den Term $(x^{3}-x^{2})$ subtrahieren wir von den höchsten Gliedern des Polynoms und beachten dabei die Klammern und Vorzeichen:
Zu dem erhaltenen Rest $x^{2}$ ziehen wir den Term der nächstniedrigeren Ordnung herunter:
Nun beginnen wir wieder mit dem ersten Schritt: Wir dividieren den höchsten Term $-x^{2}$ durch $x$ und erhalten
Wir ziehen das letzte Glied herunter und dividieren ein weiteres Mal: $6x:x=6$. Das Ergebnis der Division addieren wir rechts und multiplizieren damit den Divisor: $(x-1) \cdot 6 = 6x-6$. Subtrahieren wir diesen Term unten, so bleibt kein Rest. Die Polynomdivision ist also gelöst. Wir schreiben das Ergebnis noch einmal auf:
$(x^{3}-2x^{2}-5x+6):(x-1) = x^{2}-x-6$
Das Ergebnis der Polynomdivision ist der gesuchte quadratische Faktor für die Zerlegung des kubischen Polynoms. Die Zerlegung können wir jetzt so aufschreiben:
$x^{3}-2x^{2}-5x+6=(x-1) \cdot (x^{2}-x-6)$
Die Nullstellen des quadratischen Faktors $q(x)=x^{2}-x-6$ sind die beiden weiteren Lösungen $x_2$ und $x_3$ der kubischen Gleichung. Die Lösungen der Gleichung $x^{2}-x-6=0$ kannst du mit der $p$-$q$-Formel oder mit der Mitternachtsformel oder mit dem Satz von Vieta bestimmen und erhältst:
$x_{2} =3$ und $x_{3}=-2$
Die Lösungsmenge der kubischen Gleichung lautet also:
$\mathbb L = \{x_{1}=1; x_{2}=3; x_{3}=-2\}$
Lösungen kubischer Gleichungen graphisch darstellen
Zu der kubischen Gleichung $x^{3}-2x^{2}-5x+6=0$ betrachten wir die Polynomfunktion dritten Grades
Die Lösungen der kubischen Gleichung $x^{3}-2x^{2}-5x+6$ sind genau die Nullstellen $x_{1}=1$, $x_{2}=3$ und $x_{3}=-2$ der Polynomfunktion $f(x) = x^{3}-2x^{2}-5x+6$.
Das Video zu Gleichungen 3. Grades
In diesem Video wird dir verständlich erklärt, was kubische Gleichungen sind und wie man sie löst. Du erfährst, wie du mittels Polynomdivision eine Gleichung dritten Grades auf eine quadratische und eine lineare Gleichung zurückführen kannst. Dein neues Wissen kannst du in interaktiven Aufgaben gleich ausprobieren!
Transkript Gleichungen 3. Grades lösen – Polynomdivision
Du hast Polynomfunktionen ersten Grades schon kennengelernt? - Geradengleichungen sind okay! Polynomfunktionen zweiten Grades, also quadratische Gleichungen, können dich auch nicht mehr umhauen? Basiswerkzeuge wie die p-q-Formel oder die Mitternachtsformel sind dir geläufig? Aber wie sieht es mit höheren Polynomgleichungen aus? Um Polynomgleichungen dritten Grades mit Absolutglied zu lösen, lernst du in diesem Video die Polynomdivision kennen. Eine Gleichung 3. Grades erkennst du daran, dass der höchste Exponent von x drei ist. Eine solche Gleichung wird auch kubische Gleichung genannt. Sie besteht allgemein aus dem kubischen Glied, dem quadratischen, dem linearen und dem Absolutglied, was auch konstantes Glied genannt wird. Lass uns nun die möglichen Lösungen einer solchen Gleichung ansehen und davon ausgehen, dass wir für x nach Reellwertigen Lösungen suchen. Am Grad der Polynomgleichung erkennst du allgemein die maximale Anzahl an Lösungen! Wie am zugehörigen Funktionsgraphen jeweils zu erkennen ist, haben Polynomgleichungen ersten Grades maximal eine Lösung, Polynomgleichungen zweiten Grades maximal zwei Lösungen und Polynomgleichungen dritten Grades? Maximal drei Lösungen! Genauer gesagt haben sie entweder drei Lösungen, zwei Lösungen oder ein Lösung. Zumindest eine Lösung besitzt aber jede kubische Gleichung. Gehen wir einmal die groben Schritte zum Lösen einer kubischen Gleichung durch. Nach dem Fundamentalsatz der Algebra, lässt sich jedes kubische Polynom zerlegen in einen sogenannten Linear-Faktor und einen quadratischen Faktor. Hat dein Lehrer dir schon einmal vom Satz vom Nullprodukt erzählt? Du hast hier ein Produkt vor dir, das Null ergibt, deshalb muss DER Faktor Null sein oder DER Faktor. Von den möglichen drei Lösungen der kubischen Gleichung versteckt sich im Linearfaktor die erste Lösung "x 1". Zum Abschluss untersuchst du noch den quadratischen Faktor nach den beiden möglichen weiteren Lösungen. Aber wie kommen wir denn von der kubischen Gleichung zu diesen Faktoren? Du kannst das in zwei Schritten herausfinden: Dein erster Schritt hierbei ist die Ermittlung der ersten Lösung "x 1" und der zweite Schritt ist die Polynomdivision. Lass uns nach diesem Muster zusammen die kubische Gleichung lösen! Wir wollen also die erste Lösung "x 1" bestimmen. Dafür notieren wir vom Absolutglied die Teiler, sowie die Teiler mit negativem Vorzeichen. Die setzen wir nun probeweise für x ein und schauen, ob Null herauskommt. Wir haben Glück! Denn direkt der erste Wert "1" ist eine Lösung der kubischen Gleichung! Die Lösung halten schon einmal fest. Damit machen wir uns an die Polynomdivision, teilen also das gegebene kubische Polynom durch den Linearfaktor. Dabei ist "x 1" unsere erste Lösung. Also los: Wir teilen das höchste Glied durch x. Dafür stellst du dir am besten vor: "WAS mal x" ergibt das höchste Glied? Mit diesem Ergebnis müssen wir Rück-multiplizieren und zwar mit "x" und mit "minus 1". Den erhaltenen Term ziehen wir von unserem Polynom ab, wobei wir immer auf die Minusklammer achten! Zu dem erhaltenen Rest ziehen wir das nächste Glied herunter. Und wieder von vorne: Wir fragen uns: "WAS mal x" ergibt das höchste Glied? Mit unserem Ergebnis multiplizieren wir zurück einmal mit x und noch einmal mit "minus 1". Den erhaltenen Term ziehen wir ab, wobei wir wieder auf die Minusklammer achten! Zu dem erhaltenen Rest ziehen wir das nächste Glied herunter. Und ein drittes Mal: "WAS mal x" ergibt das höchste Glied? Mit dem Ergebnis multiplizieren wir mit "x" zurück und mit "minus 1". Beim Abziehen achten wir wieder auf die Minusklammer. Der Rest ist Null! Wir haben den quadratischen Faktor bestimmt! Das kubische Polynom geteilt durch den Linearfaktor ergibt also diesen quadratischen Faktor. Diese Zeile können wir als Gleichung ansehen, in der wir auf beiden Seiten mit dem Linearfaktor multiplizieren. Demnach zerlegt sich das kubische Polynom genau in dieses Produkt. Unsere eigentliche kubische Gleichung, können wir mit dieser Hilfe also auch anders darstellen. Jetzt erinnern wir uns an den Satz vom Nullprodukt. Die Lösung aus dem linearen Faktor haben wir schon als "x 1" bestimmt. Diese quadratischen Gleichung enthält nun die mögliche zweite und dritte Lösung der kubischen Gleichung. Für die Lösung benutzt du zum Beispiel die p-q-Formel, die Mitternachts-Formel oder den Satz von Vieta. Wir gelangen hier so oder so zu zwei weiteren Lösungen der kubischen Gleichung. Ergänzend können wir uns noch die graphische Darstellung der Lösungen anschauen. Betrachten wir von dem zugehörigen kubischen Polynom den Funktionsgraphen, dann entsprechen die drei Lösungen unser Gleichungen genau diesen drei Nullstellen! Lass uns das alles zusammenfassen. Eine Funktion 3. Grades mit Absolutglied löst du so: Die erste Lösung bestimmst du mithilfe der Teiler des absoluten Glieds. Danach führst du die Polynomdivision durch, um den quadratischen Faktor zu ermitteln. Deine kubische Gleichung kannst du nun mit Faktoren schreiben. Nach dem Satz vom Nullprodukt musst du den quadratischen Faktor gleich null setzen. Dann erhältst du die möglichen weiteren beiden Nulstellen. Die Lösungsmenge besteht immer insgesamt aus mindestens einer und höchstens drei Lösungen. Hey, super, dass du durchgehalten hast!Gönn dir doch eine kleine Pause und mach's wie Julia die denkt nach einer Gleichung dritten Grades gern an 30 Grad und Palmenstrand!
Gleichungen 3. Grades lösen – Polynomdivision Übung
-
Gib eine Lösung der Gleichung dritten Grades an.
TippsDie Teiler einer ganzen Zahl $n$ sind alle ganzen Zahlen, durch die sich $n$ ohne Rest teilen lässt.
Die Teiler von $15$ sind $1$, $3$, $5$ und $15$.
Den Linearfaktor, durch den du das Polynom $f$ teilen kannst, ist von der Form $(x-x_1)$. Hierbei ist $x_1$ die zuvor bestimmte Nullstelle von $f$.
LösungDas Polynom $x^3 -2x^2 -5x +6=0$ ist dritten Grades und hat daher mindestens eine Nullstelle. Oft ist ein Teiler des Absolutgliedes oder das Negative eines Teilers eine Nullstelle.
Das Absolutglied des Polynoms ist der konstante Term $6$. Die Teiler von $6$ sind $1$, $2$, $3$ und $6$. Die Negativen der Teiler sind $-1$, $-2$, $-3$ und $-6$.
Um eine Lösung der Gleichung dritten Grades zu finden, setzen wir die Teiler des Absolutglieds und ihre Negativen in das Polynom ein. Für $x=-1$ erhalten wir:
$f(-1)= (-1)^3 -2\cdot (-1)^2 -5 \cdot (-1) + 6 = -1 -2 \cdot 1 - 5 \cdot (-1) + 6 = 8$
Für $x=1$ erhalten wir:
$f(1)= 1^3 -2\cdot 1^2 -5 \cdot 1 + 6 = 1 -2 \cdot 1 - 5 \cdot 1 + 6 = 0$
Damit ist $x=1$ eine Nullstelle. Der zugehörige Linearfaktor ist:
$(x-1)$
Durch diesen Linearfaktor kann man das Polynom dividieren, um weitere Nullstellen zu finden.
-
Benenne die Eigenschaften der Polynome.
TippsEine lineare Funktion hat genau eine Nullstelle.
Die Gleichung $x^2-x-2=0$ hat zwei Lösungen.
Ist $a \cdot b =0$, so ist $a=0$ oder $b=0$.
LösungWir betrachten die Lösungen einer Gleichung höheren Grades. Die Lösungen einer solchen Gleichung sind die Nullstellen eines Polynoms $f$. Hat das Polynom $f$ den Grad $n$, so nennt man die Gleichung $f(x)=0$ eine Gleichung $n$-ten Grades.
Der Grad des Polynoms ist die höchste vorkommende Potenz der Variablen $x$. Ein Polynom vom Grad $n$ hat höchstens $n$ Nullstellen. Am Funktionsgraphen eines Polynoms zweiten oder dritten Grades kann man erkennen, dass ein solches Polynom auch weniger Nullstellen haben kann.
Ist der Grad einer Gleichung eine ungerade Zahl, hat die Gleichung mindestens eine Lösung. Das trifft also für Gleichungen ersten und dritten Grades zu, aber nicht für Gleichungen zweiten Grades.
Den Satz vom Nullprodukt benutzt man, um aus der Zerlegung eines Polynoms dritten Grades in einen Linearfaktor und einen quadratischen Faktor die Nullstellen zu bestimmen: Ist das Produkt $0$, muss einer der Faktoren $0$ sein. Das heißt, die Nullstellen des kubischen Polynoms sind die Nullstellen des quadratischen und linearen Faktors.
Demnach sind folgende Aussagen richtig:
- Eine Gleichung dritten Grades hat mindestens eine Lösung.
- Eine Gleichung dritten Grades hat höchstens drei Lösungen.
- Der Satz vom Nullprodukt besagt: Ein Produkt ist $0$, wenn einer der Faktoren $0$ ist.
- Der Grad einer Polynomgleichung ist die maximale Anzahl der Lösungen.
Dagegen sind folgende Aussagen falsch:
- Eine Gleichung dritten Grades hat genau drei Lösungen.
- In einer Gleichung dritten Grades ist der höchste Exponent von $x$ mindestens $3$.
- Die Anzahl der Lösungen einer Polynomgleichung ist die Anzahl der Glieder des Polynoms.
-
Ermittle den quadratischen Faktor.
TippsFühre die Polynomdivision wie in diesem Beispiel durch: Dividiere den Term höchster Potenz in dem Polynom durch den Term der höchsten Potenz im Teiler. Multipliziere das Ergebnis der Division dann mit dem Teiler $(x-1)$ und subtrahiere dieses Ergebnis von dem zu teilenden Polynom.
Beginne die Polynomdivision ähnlich wie die Division von Dezimalzahlen mit dem höchsten Term, d. h. mit dem Term höchster Potenz. Dividiere $x^3$ durch $x$ und notiere das Resultat hinter dem Gleichheitszeichen.
Multipliziere das Ergebnis der Division mit dem Teiler $(x-1)$ und trage dies in die zweite Zeile ein. Subtrahiere die zweite Zeile von der ersten und beginne dann wieder mit der Division durch $x$.
LösungBei der Polynomdivision gehst du folgendermaßen vor:
Du dividierst zuerst den Term mit höchsten Potenz, also $x^3$, durch $x$ und schreibst das Ergebnis, also $x^2$, hinter das Gleichheitszeichen.
Jetzt multiplizierst du dieses $x$ mit dem Teiler $(x-1)$ und erhältst $x^3-x^2$. Das schreibst du in die zweite Zeile unter die beiden ersten Terme des Polynoms $x^3 -2x^2 -5x +1$.
Dann subtrahierst du $x^3-x^2$ von $x^3 -2x^2 -5x +1$. In die dritte Zeile schreibst du von dem Ergebnis der Subtraktion die beiden Terme höchster Potenz.
Danach verfährst du wieder wie zuvor: Division durch $x$, Notieren des Ergebnisses, Multiplikation mit $(x-1)$ und Subtraktion. So verfährst du, bis kein Term mehr übrig ist, den du noch durch $x$ dividieren kannst.Die vollständige Polynomdivision sieht wie folgt aus:
$\begin{array}{ccccc clcl} &(x^3& -2x^2& -5x& +1)&:&(x-1)&=&x^2 -x +6\\ -&(x^3 & -x^2) \\ &&\phantom{(}-x^2 &-5x\\ &-&(-x^2 & +x)\\ & & &-6x &+1 \\ & & -&\phantom{(}(-6x&+1) \\ \end{array}$
-
Erschließe die zugehörigen Faktoren.
TippsFühre die Polynomdivisionen mit dem Linearfaktor $(x-1)$ wie in diesem Beispiel durch. Zur Erinnerung wird hier in dem Bild der Anfang der Polynomdivision gezeigt.
Das Absolutglied des kubischen Polynoms ist das Produkt aus den Absolutgliedern des quadratischen und des linearen Faktors. Damit kannst du prüfen, ob du die Polynomdivision richtig durchgeführt hast.
Der Koeffizient des kubischen Terms ist das Produkt der Terme mit der jeweils höchsten Potenz in dem quadratischen und dem linearen Faktor. Hiermit kannst du ebenfalls die Polynomdivision überprüfen.
Zum Beispiel ist $2x^3-x^2-2x+1$ nicht das Produkt aus dem quadratischen Faktor $x^2-x-6$ und dem Linearfaktor $x-1$, weil der Koeffizient von $x^3$ ja $2$ ist, das Produkt der Koeffizienten von $x^2$ aus dem quadratischen Faktor und $x$ aus dem Linearfaktor aber $1$.
LösungWir führen die einzelnen Polynomdivisionen mit dem Linearfaktor $(x-1)$ durch:
Zuerst dividieren wir den Term höchster Potenz, also den $x^3$-Term durch $x$, und notieren das Ergebnis hinter dem Gleichheitszeichen.
Dieses Ergebnis multiplizieren wir mit dem Linearfaktor $(x-1)$, schreiben es in die zweite Zeile und subtrahieren von dem Polynom.
Wir erhalten in der dritten Zeile ein neues Polynom, so dass wir wieder von vorn beginnen können mit Division durch $x$, Notieren des Ergebnisses, Multiplikation mit $(x-1)$ und Subtraktion.
In dieser Weise verfahren wir, bis keine Terme mehr übrig sind, die wir durch $x$ dividieren können.Die Polynomdivisionen im Einzelnen sehen dann so aus:
Für das Polynom $f(x)=x^3-2x^2-5x+6$ finden wir:
$\begin{array}{ccccc clcl} &(x^3& -2x^2& -5x& +1)&:&(x-1)&=&x^2 -x -6\\ -&(x^3 & -x^2) \\ &&\phantom{(}-x^2 &-5x\\ &-&(-x^2 & +x)\\ & & &-6x &+1 \\ & & -&\phantom{(}(-6x&+1) \\ & & & & 0 \end{array}$
Für das Polynom $g(x)= 2x^3-x^2-2x+1$ ist das die Rechnung:
$\begin{array}{ccccc clcl} &(2x^3& -x^2& -2x& +1)&:&(x-1)&=&2x^2+x-1\\ -&(2x^3 & -2x^2) \\ &&\phantom{(} x^2 &-2x\\ &-&(x^2 & -x)\\ & & &-x &+1 \\ & & -&\phantom{(}(-x&+1) \\ & & & & 0 \end{array}$
Das Polynom $h(x)=x^3-4x^2+7x-4$ führt auf folgende Division:
$\begin{array}{ccccc clcl} &(x^3& -4x^2& +7x& -4)&:&(x-1)&=&x^2-3x + 4\\ -&(x^3 & -x^2) \\ &&\phantom{(}-3x^2 &+7x\\ &-&(-3x^2 & +3x)\\ & & &4x &-4 \\ & & -&\phantom{(}(4x&-4) \\ & & & & 0 \end{array}$
Schließlich erhalten wir für das Polynom $k(x)=2x^3-3x^2+2x-1$ diese Division:
$\begin{array}{ccccc clcl} &(2x^3& -3x^2& +2x& -1)&:&(x-1)&=&2x^2 -x +1 \\ -&(2x^3 & -2x^2) \\ &&\phantom{(}-x^2 &+2x\\ &-&(-x^2 & +x)\\ & & &x &-1 \\ & & -&\phantom{(}(x&-1) \\ & & & & 0 \end{array}$
-
Benenne die Glieder der Polynome.
TippsQuadratische Terme sind durch die zweite Potenz bestimmt.
Lineare Terme sind nicht konstant.
Konstant bedeutet „nicht veränderlich“ bzw. „ständig gleichbleibend“.
LösungEin kubisches Polynom ist ein Polynom, bei dem $x^3$ die höchste Potenz der Variablen $x$ ist. Bei einem kubischen Polynom sortiert man die Glieder nach Potenzen der Variablen $x$.
Das kubische Glied besteht aus allen kubischen Termen, d. h. Termen der Form $x^3$ multipliziert mit einem Koeffizienten.
Das quadratische Glied enthält alle quadratischen Glieder, d. h. Terme der Form $x^2$ multipliziert mit Koeffizienten.
Das lineare Glied besteht aus den linearen Termen. Diese sind Terme der Form $x$ multipliziert mit Koeffizienten.
Das Absolutglied schließlich besteht aus allen konstanten Termen.Die Glieder der beiden angegebenen Polynome sind also:
kubisches Glied:
- $ax^3$
- $x^3$
- $bx^2$
- $-2x^2$
- $cx$
- $-5x$
- $d$
- $6$
-
Erschließe den quadratischen Faktor.
TippsDas Produkt der Absolutglieder des quadratischen und des linearen Faktors ist das Absolutglied des kubischen Polynoms.
Dividiere $x^3$ durch $x$, um das quadratische Glied des quadratischen Faktors zu bestimmen.
LösungFür die Polynomdivision ergänzen wir zunächst das Polynom $x^3 + 1$ zu $x^3 + 0x^2 + 0x +1$. Dann führen wir die Polynomdivision durch: Division von $x^3$ durch $x$ liefert $x^2$. Multiplikation von $x^2$ mit $(x-1)$ ergibt $x^3-x^2$. Wir subtrahieren dann $x^3-x^2$ von $x^3-0x^2$ und erhalten $x^2 + 0x^1$. Damit verfahren wir wie am Anfang: Division durch $x$, Multiplikation des Ergebnisses mit $(x-1)$, Subtraktion von $x^2+0x^1$ usw.
Die vollständige Polynomdivision sieht dann so aus:
$ \begin{array}{ccccc clcl} &(x^3& 0x^2& 0x^1& +1)&:&(x+1)&=&x^2 -x +1\\ -&(x^3 & +x^2) \\ &&\phantom{(}-x^2 &\\ &-&(-x^2 & -x)\\ & & &x &+1 \\ & & -&\phantom{(}(x&+1) \\ & & & & 0 \end{array} $
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Primzahlen
- Geometrische Lagebeziehungen
- Rechteck
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Quadrat
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Was Ist Eine Viertelstunde
- Prisma
- Mitternachtsformel
- Grundrechenarten Begriffe
- Dreiecksarten
- Quader
- Satz Des Pythagoras
- Dreieck Grundschule
- Erste Binomische Formel
- Kreis
- Standardabweichung
- Flächeninhalt
- Volumen Kugel
- Zahlen In Worten Schreiben
- Meter
- Orthogonalität
- Schriftlich Multiplizieren
- Brüche Multiplizieren
- Potenzgesetze
- Distributivgesetz
- Flächeninhalt Dreieck
- Rationale Zahlen
- Volumen Berechnen
- Brüche Addieren
- Kongruenz
- Exponentialfunktion
- Scheitelpunktform
- Logarithmus
- Erwartungswert
- Skalarprodukt
- Primfaktorzerlegung
- Quadratische Ergänzung
- Zinseszins
- Geradengleichung Aus Zwei Punkten Bestimmen
- Sinusfunktion
 Du möchtest schneller & einfacher lernen?
Du möchtest schneller & einfacher lernen?

 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen







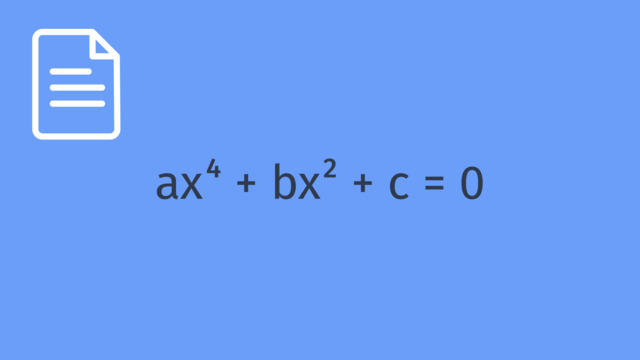









Hallo Sandraaugustin,
du subtrahierst an dieser Stelle von dem Term -x^2-5x den Term -x^2+x. Dann erhältst du folgende Aufgabe:
-x^2-5x-(-x^2+x)
Du musst hier die Minusklammer beachten, da sich dadurch alle Zeichen innerhalb der Klammer umkehren:
-x^2-5x+x^2-x=-5x-x=-6x
Hoffentlich konnten wir dir helfen.
Liebe Grüße aus der Redaktion
Hallo eine Frage habe ich noch: Wie komme ich bei Minute 4:36, -6x raus? Wie genau gehe ich da nochmal vor?