Gebrochenrationale Funktionen – Rekonstruktion
Sind einige Eigenschaften einer gebrochenrationalen Funktion bekannt, so kann die Funktionsgleichung rekonstruiert werden.
Inhaltsverzeichnis zum Thema
- Was ist eine gebrochenrationale Funktion?
- Was ist eine Rekonstruktion?
- Eigenschaften von gebrochenrationalen Funktionen
- Die Rekonstruktion an einem Beispiel
Was ist eine gebrochenrationale Funktion?
Eine gebrochenrationale Funktion $f$ sieht so aus:
$f(x)=\frac{Z(x)}{N(x)}=\dfrac{a_nx^n+...+a_1x+a_0}{b_mx^m+...+b_1x+b_0}$
Du siehst, sowohl im Zähler ($Z(x)$) als auch im Nenner ($N(x)$) steht eine ganzrationale Funktion (oder auch Polynom).
Der Zählergrad ist $n$ und der Nennergrad $m$. Diese müssen nicht übereinstimmen.
Beachte, dass eine gebrochenrationale Funktion nicht für alle Zahlen definiert ist. Da die Division durch $0$ nicht erlaubt ist, musst du den Term im Nenner, also $N(x)$, auf Nullstellen untersuchen. Diese musst du aus dem Definitionsbereich ausschließen.
Was ist eine Rekonstruktion?
Bei einer Kurvendiskussion betrachtest du eine gegebene Funktion und untersuchst den zugehörigen Funktionsgraphen auf Schnittstellen mit den Koordinatenachsen, Extrema, Wendepunkte und so weiter. Schließlich kannst du unter Zuhilfenahme der gefundenen Ergebnisse den Funktionsgraphen zeichnen.
Umgekehrt könntest du auch Informationen, zum Beispiel Symmetrie, Position von Nullstellen, spezielle Punkte des Funktionsgraphen kennen. Es geht dann darum, die Funktionsgleichung wiederherzustellen, sprich zu rekonstruieren.
Oft musst du bei einer solchen Aufgabe die Informationen aus einem Text oder einem Sachzusammenhang ermitteln. Häufig werden diese Art von Aufgaben Steckbriefaufgaben genannt, da wie bei einem Steckbrief Eigenschaften genutzt werden, um etwas zu finden.
Im Folgenden schauen wir uns an, wie du solche Informationen in mathematische Gleichungen übersetzen kannst. Abschließend siehst du an einem Beispiel, wie solch eine Rekonstruktion durchgeführt wird.
Eigenschaften von gebrochenrationalen Funktionen
Um Funktionsgleichungen zu rekonstruieren, musst du Eigenschaften der betrachteten Funktionenklasse kennen. Deshalb siehst du hier einige dieser Eigenschaften. Es gibt natürlich noch sehr sehr viele weitere solcher Eigenschaften.
Nullstellen
Eine gebrochenrationale Funktion hat eine Nullstelle, zum Beispiel bei $x=3$, wenn $Z(3)=0$ gilt. Du kannst also $Z(x)=(x-3)\cdot p(x)$ mit einem beliebigen Polynom $p$ ansetzen.
Polstellen
Eine Polstelle ist eine nicht hebbare Definitionslücke. Hier liegt eine senkrechte Asymptote vor. Wenn es zum Beispiel bei $x=2$ eine Polstelle gibt, weißt du, dass $N(2)=0$ gilt. Somit gilt $N(x)=(x-2)\cdot q(x)$ mit einem beliebigen Polynom $q$.
Waagerechte Asymptoten
Hat eine ganzrationale Funktion eine waagerechte Asymptote $y=c\neq 0$, so gilt, dass Zählergrad und Nennergrad übereinstimmen, also $n=m$.
Übrigens: Wenn die $x$-Achse, also $y=0$, eine waagerechte Asymptote ist, ist der Zählergrad kleiner als der Nennergrad, also $n\lt m$:
Extrema und Wendepunkte
Hierfür musst du schon ein paar Informationen haben. Sei zum Beispiel $f$ gegeben mit $f(x)=\frac{ax+b}{cx^2}$. Du musst nun die erste beziehungsweise zweite Ableitung bestimmen. Wenn du eine Extrem- oder Wendestelle kennst, weißt du, dass die entsprechende Ableitung an dieser Stelle $0$ sein muss.
Die Rekonstruktion an einem Beispiel
Eine gebrochenrationale Funktion hat eine Nullstelle bei $x=1$ sowie eine senkrechte Asymptote bei $x=0$ und eine waagerechte bei $y=4$. Der Zählergrad sei $1$.
- Die Nullstelle: Es gilt $Z(x)=k\cdot (x-1)$.
- Die senkrechte Asymptote: Damit erhältst du $N(x)=x\cdot q(x)$.
- Die waagerechte Asymptote liefert die Information, dass auch der Nennergrad $1$ ist, also ist $q(x)$ konstant. Der Einfachheit halber nehmen wir an, dass $q(x)=1$ ist, andernfalls kannst du kürzen. Weiter kannst du mit der waagerechten Asymptote $y=4$ herleiten, dass $k=4$ sein muss.
Nun hast du folgende Funktionsgleichung rekonstruiert:
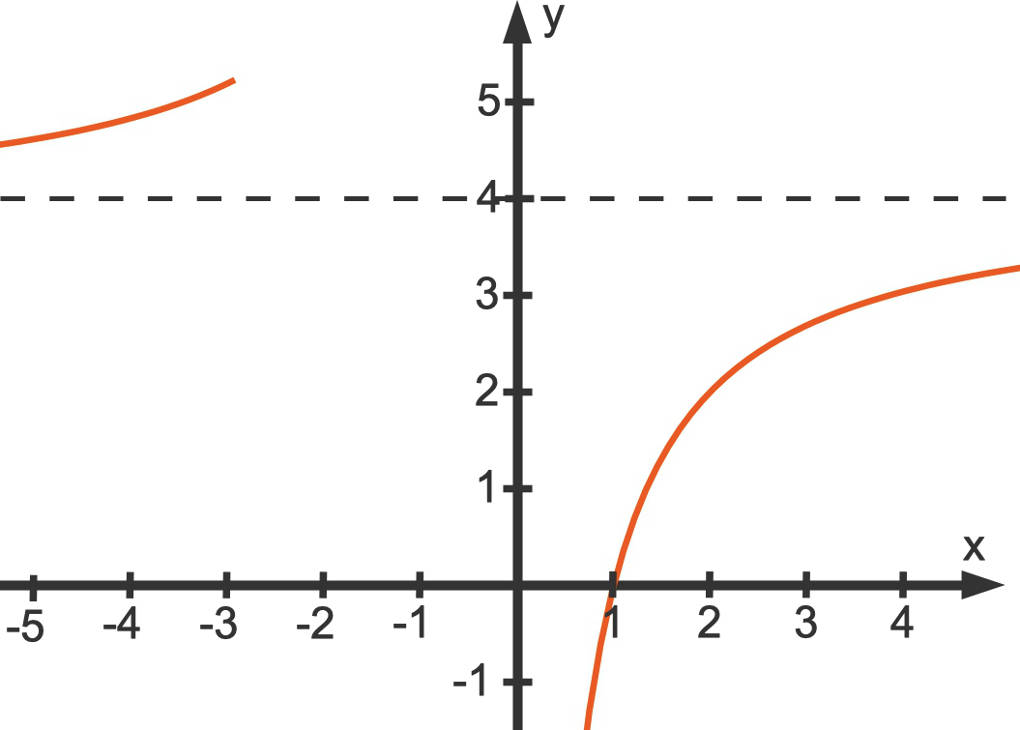
$f(x)=\frac{4(x-1)}{x}$
Den zugehörigen Funktionsgraphen siehst du hier:
Alle Videos zum Thema
Videos zum Thema
Gebrochenrationale Funktionen – Rekonstruktion (2 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Gebrochenrationale Funktionen – Rekonstruktion (2 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Primzahlen
- Geometrische Lagebeziehungen
- Rechteck
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Quadrat
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Was Ist Eine Viertelstunde
- Prisma
- Mitternachtsformel
- Grundrechenarten Begriffe
- Dreiecksarten
- Quader
- Satz Des Pythagoras
- Dreieck Grundschule
- Erste Binomische Formel
- Kreis
- Standardabweichung
- Flächeninhalt
- Volumen Kugel
- Zahlen In Worten Schreiben
- Meter
- Orthogonalität
- Schriftlich Multiplizieren
- Brüche Multiplizieren
- Potenzgesetze
- Distributivgesetz
- Flächeninhalt Dreieck
- Rationale Zahlen
- Volumen Berechnen
- Brüche Addieren
- Kongruenz
- Exponentialfunktion
- Scheitelpunktform
- Logarithmus
- Erwartungswert
- Skalarprodukt
- Primfaktorzerlegung
- Quadratische Ergänzung
- Zinseszins
- Geradengleichung Aus Zwei Punkten Bestimmen
- Sinusfunktion



 Rekonstruktion gebrochenrationaler Funktionen
Rekonstruktion gebrochenrationaler Funktionen
 Rekonstruktion gebrochenrationaler Funktionen – Beispiel
Rekonstruktion gebrochenrationaler Funktionen – Beispiel









