Flächeneinheiten umrechnen
In vielen Aufgaben in der Geometrie musst du Flächen bestimmen, genauer den Inhalt dieser Flächen. Wenn du solche Flächen vergleichen möchtest, müssen sie in der gleichen Flächeneinheit vorliegen.
Beliebteste Videos
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Flächeninhalte berechnen
- Flächeneinheiten
- Flächeneineinheiten umrechnen
- Warum müssen Flächeneinheiten umgerechnet werden?
Flächeninhalte berechnen
Schau dir dieses Rechteck an.
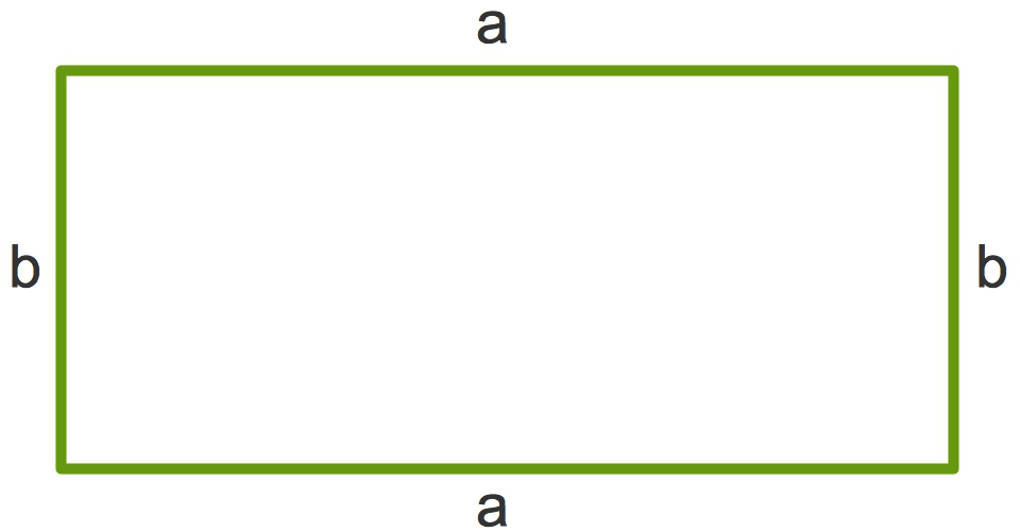
Du kannst den Flächeninhalt eines Rechtecks berechnen, indem du die Längen der beiden Seiten, hier $a$ und $b$, multiplizierst. So erhältst du $A=a\cdot b$. Dabei steht $A$ für den Flächeninhalt.
Du lernst das Berechnen von Flächeninhalten für viele verschiedene geometrische Figuren, zum Beispiel Parallelogramme, Drachen und Rauten, Trapeze, ...
Die Maßeinheit für einen Flächeninhalt ist eine Flächeneinheit. Es gibt, genauso wie bei Längen, verschiedene Einheiten für Flächen. Im Folgenden geht es darum, wie du diese umrechnen kannst.
Flächeneinheiten
Nun weißt du bereits, dass Flächen, wie beispielsweise das oben abgebildete Rechteck, einen Flächeninhalt haben. Dieser wird in Flächeneinheiten angegeben.
Wir wiederholen einmal kurz die Längeneinheiten. Diese sind Millimeter ($\text{mm}$), Zentimeter ($\text{cm}$), Dezimeter ($\text{dm}$), Meter ($\text{m}$) und Kilometer ($\text{km}$). Je nachdem, was du misst, verwendest du die entsprechende Längeneinheit.
So ist das auch bei Flächeneinheiten. Bei diesen steht noch eine kleine $2$ als Hochzahl. Du sagst dann Quadrat-.
Wie kannst du dir Flächeneinheiten merken? Du stellst dir immer etwas aus deiner Umgebung vor, was die entsprechende Flächeneinheit hat. Hier siehst du einige Beispiele. Vielleicht fallen dir ja noch weitere ein.
- Quadratmillimeter ($\text{mm}^{2}$): Ein flacher Stecknadelkopf hat einen Flächeninhalt von $1~\text{mm}^{2}$.
- Quadratzentimeter ($\text{cm}^{2}$): Schau dir deinen Daumennagel an. Dieser hat einen Flächeninhalt von $1~\text{cm}^{2}$.
- Quadratdezimeter ($\text{dm}^{2}$): Eine CD-Hülle hat einen Flächeninhalt von etwa $1~\text{dm}^{2}$.
- Quadratmeter ($\text{m}^2$): Ein quadratischer Tisch, der eine Seitenlänge von $1~\text{m}$ hat, hat den Flächeninhalt $1~\text{m}^2$. Zum Beispiel werden Wohnungen in Quadratmeter angegeben, zum Beispiel $88~\text{m}^2$.
- Ein Ar ($a$) ist das Gleiche wie $100~\text{m}^2$.
- Ein Hektar ($ha$) ist das Gleiche wie $10000~\text{m}^2$. Mit Ar oder Hektar werden zum Beispiel Waldflächen angegeben.
- Quadratkilometer ($\text{km}^2$): Berlin hat ungefähr eine Fläche von $892~\text{km}^2$.
Wie kannst du nun diese Flächeneinheiten umrechnen?
Flächeneineinheiten umrechnen
Als Wiederholung siehst du hier, wie du Längeneinheiten umrechnen kannst:
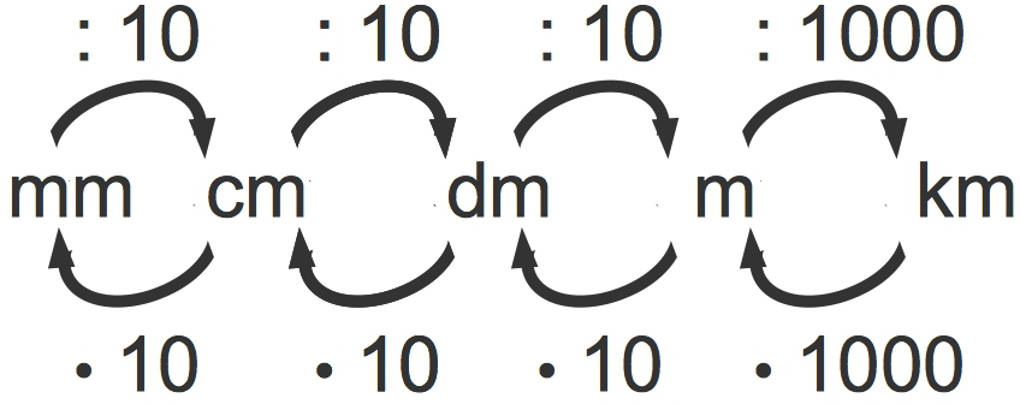
Nun schauen wir uns einmal an, wie $\text{mm}^{2}$ in $\text{cm}^{2}$, also Flächeneinheiten umgerechnet werden können.
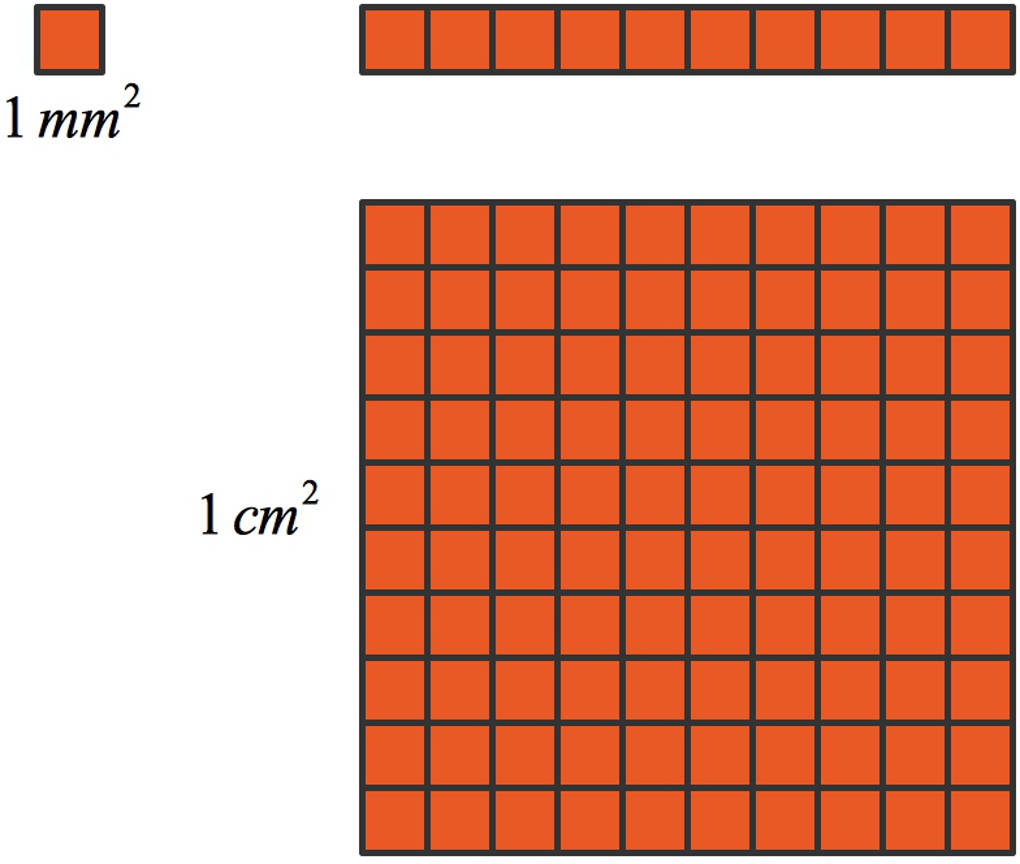
- Oben links siehst du einen Quadratmillimeter.
- Du weißt bereits, dass $10~\text{mm}=1~\text{cm}$ sind. Wenn du $10$ Quadratmillimeter nebeneinander legst, das siehst du auch oben, kommst du aber noch nicht zu einem Quadratzentimeter.
- Du musst insgesamt $10$ solcher $10$-er Reihen hinlegen. Das sind dann zusammen $10\cdot 10=10^{2}=100$ Quadratmillimeter. Du quadrierst also den Umrechnungsfaktor, welchen du von den Längeneinheiten bereits kennst.
- Somit sind $100~\text{mm}^{2}=1~\text{cm}^{2}$. Anders ausgedrückt: Um von Quadratmillimeter auf Quadratzentimeter zu kommen, musst du durch $100$ dividieren. Umgekehrt von Quadratzentimeter auf Quadratmillimeter musst du mit $100$ multiplizieren.
Zusammenfassend siehst du die Umrechnungen hier:
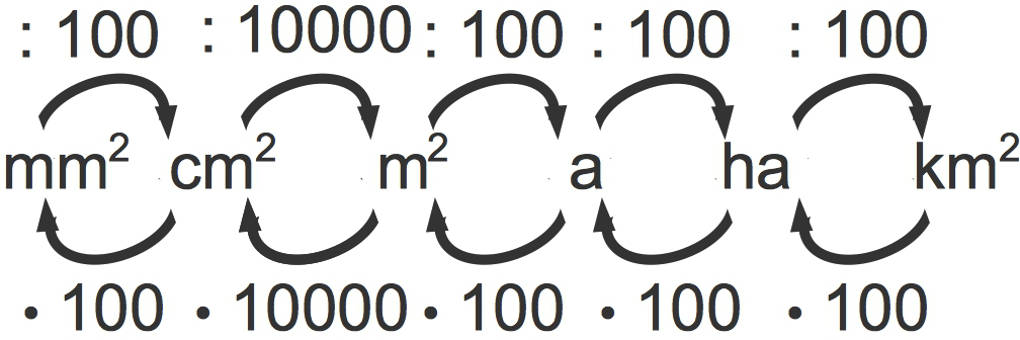
Merke dir, wie bei allen Umrechnungen von Einheiten: Möchtest du von einer kleineren auf eine größere Einheit umrechnen, musst du dividieren. Umgekehrt von einer größeren auf eine kleinere Einheit musst du multiplizieren.
Nun kannst du auch Einheiten überspringen. Du kannst zum Beispiel schauen, wie Quadratzentimeter in Quadratmeter umgerechnet werden.
- Von Quadratzentimeter zu Quadratdezimeter dividierst du durch $100$.
- Von Quadratdezimeter zu Quadratmeter dividierst du wieder durch $100$.
- Insgesamt dividierst du also durch $100\cdot 100=10000$.
Umgekehrt übrigens multiplizierst du mit $10000$.
Lass uns das doch einmal an Beispielen üben.
Beispiel - Tischplatte
Eine Tischplatte ist $80~\text{cm}$ lang und $50~\text{cm}$ breit. Der Flächeninhalt dieser Tischplatte beträgt $80~\text{cm}\cdot 50~\text{cm}=4000~\text{cm}^{2}$.
Wie viele Quadratmeter sind das? Hierzu dividierst du durch $10000$. Du rechnest $4000:10000=0,4$. Die Tischplatte hat also einen Flächeninhalt von $0,4~\text{m}^{2}$.
Beispiel - Hamsterhaus
Tim möchte ein Hamsterhaus bauen. Die Grundfläche ist quadratisch mit der Seitenlänge $0,8~\text{m}$. Tim berechnet den Flächeninhalt in Quadratmeter zu $(0,8~\text{m})^{2}=0,64~\text{m}^{2}$.
Nun fragt er sich, wie viele Quadratzentimeter das sind. Er multipliziert mit $10000$ und erhält so $6400~\text{cm}^{2}$.
Warum müssen Flächeneinheiten umgerechnet werden?
Du kannst Flächeninhalte nur dann vergleichen, addieren oder subtrahieren, wenn sie in einer gemeinsamen Einheit vorliegen.
Schauen wir uns ein abschließendes Beispiel an. Tim überlegt, welche Fläche größer ist. Er vergleicht den Tisch mit $4000~\text{cm}^{2}$ und die Grundfläche des Hamsterhauses mit $0,64~\text{m}^{2}$. Hmmmm, er überlegt. Die eine Fläche ist in Quadratzentimeter und die andere in Quadratmeter angegeben. Er hat aber bereits die Grundfläche des Hamsterhauses in Quadratzentimeter umgerechnet und $6400~\text{cm}^{2}$ erhalten.
Nun kann er die beiden Größen vergleichen: $4000~\text{cm}^{2}\lt 6400~\text{cm}^{2}$. Er sieht, dass der Flächeninhalt des Tisches kleiner ist als der Flächeninhalt der Grundfläche des Hamsterhauses.
Alle Videos zum Thema
Videos zum Thema
Flächeneinheiten umrechnen (2 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Flächeneinheiten umrechnen (2 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Primzahlen
- Geometrische Lagebeziehungen
- Rechteck
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Quadrat
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Was Ist Eine Viertelstunde
- Prisma
- Mitternachtsformel
- Grundrechenarten Begriffe
- Dreiecksarten
- Quader
- Satz Des Pythagoras
- Dreieck Grundschule
- Erste Binomische Formel
- Kreis
- Standardabweichung
- Flächeninhalt
- Volumen Kugel
- Zahlen In Worten Schreiben
- Meter
- Orthogonalität
- Schriftlich Multiplizieren
- Brüche Multiplizieren
- Potenzgesetze
- Distributivgesetz
- Flächeninhalt Dreieck
- Rationale Zahlen
- Volumen Berechnen
- Brüche Addieren
- Kongruenz
- Exponentialfunktion
- Scheitelpunktform
- Logarithmus
- Erwartungswert
- Skalarprodukt
- Primfaktorzerlegung
- Quadratische Ergänzung
- Zinseszins
- Geradengleichung Aus Zwei Punkten Bestimmen
- Sinusfunktion





 Flächeneinheiten umrechnen
Flächeneinheiten umrechnen
 Mit Flächeneinheiten rechnen
Mit Flächeneinheiten rechnen









