Faktorregel bei Ableitungen

in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
Grundlagen zum Thema Faktorregel bei Ableitungen
Nach dem Schauen dieses Videos wirst du in der Lage sein, Funktionen mit Hilfe der Faktorregel abzuleiten.
Zunächst lernst du, dass ein konstanter Faktor beim Ableiten einfach stehen bleibt. Anschließend siehst du an ein paar Beispielen, was ein konstanter Faktor ist und in welchen Formen dieser auftreten kann.

Abschließend erfährst du, wie du Brüche so umformen kannst, dass du sie mit der Faktorregel ableiten kannst.
Das Video beinhaltet Schlüsselbegriffe, Bezeichnungen und Fachbegriffe wie Ableitungsfunktion, Potenzregel, konstanter Faktor und Faktorregel.
Bevor du dieses Video schaust, solltest du bereits die Potenzregel für Ableitungen kennen. Außerdem solltest du grundlegendes Wissen zu Ableitungen haben.
Nach diesem Video wirst du darauf vorbereitet sein, die Summenregel für Ableitungen zu lernen.
Transkript Faktorregel bei Ableitungen
Die Sonne geht auf! Ein weiterer Tag voller Chancen und neuer Möglichkeiten. Die Welt steht dir offen – du könntest jetzt wirklich alles machen! Zum Beispiel an deiner Karriere als professioneller Anwender der „Faktorregel bei Ableitungen“ arbeiten. Dann legen wir mal los! Die Potenzregel kennst du a schon! Wenn wir eine Potenzfunktion haben – wie diese hier – können wir sie ableiten, indem wir den Exponenten als Faktor nach vorne ziehen, und dann um eins verringern. Easy! Höchste Zeit für eine neue Herausforderung! Wie leiten wir denn diese Funktion ab? Genauer gefragt: Was passiert mit dem Faktor fünf, der vor dem x steht? Die gute Nachricht direkt vorweg: Das Ableiten ändert an diesem Faktor nichts! Das heißt: Wir müssen „x hoch drei“ ganz normal mit der Potenzregel ableiten. Die Faktorregel besagt, dass ein konstanter Faktor vor der „Potenz von x“ beim Ableiten einfach erhalten bleibt. Jetzt können wir noch multiplizieren und fertig ist unsere Ableitungsfunktion. Allgemein können wir das so festhalten: Wenn wir eine Funktion ableiten wollen, die sich aus einem Term, der ein x enthält – nennen wir ihn „u von x“ – und einem beliebigen konstanten Faktor – nennen wir ihn k – zusammensetzt, dann bleibt dieser Faktor beim Ableiten erhalten und wir müssen nur den Term ableiten, der das x enthält. Okay, das sieht auf den ersten Blick kompliziert aus. Es ergibt aber Sinn, wenn wir uns noch ein paar Beispiele anschauen. Zunächst einmal klären wir die Frage: Was ist überhaupt ein konstanter Faktor? Das kann jede beliebige reelle Zahl sein, wie zum Beispiel minus sechstausend, ein Halb, Wurzel zwei, oder einfach drei. Konstant heißt, dass der Faktor selbst kein weiteres x enthalten darf. In diesem Fall müssten wir die Produktregel anwenden und das ist ein Thema für ein anderes Video. Faktor heißt, dass wir diese Zahl mit dem x-Term multiplizieren und nicht addieren oder subtrahieren. Auch in diesem Fall würde eine andere Ableitungsregel, nämlich die Summenregel zum Einsatz kommen. Das „u von x“ kann irgendeine Funktion sein, die ein x enthält. Also zum Beispiel x Quadrat, Wurzel aus x, oder auch – für die Feinschmecker unter uns – Sinus von x. Eine Delikatesse! Wir machen aber erstmal langsam und schauen uns diese Funktion an. Wie lautet die Ableitung? Um das zu berechnen, müssen wir nur „x hoch sieben“ mit der Potenzregel ableiten, und dann beide Faktoren zusammenfassen. Und schon haben wir „F Strich von x“ berechnet. Nächstes Beispiel: Hier können wir unsere Funktion erstmal so umschreiben, dass wir den konstanten Faktor deutlich erkennen. Dann wieder den Term ableiten, der das x enthält und die Faktoren zusammenfassen. Hier kürzen sie sich gegenseitig weg. Zum krönenden Abschluss diese Funktion: Davon, dass wir hier ein T und kein x als Variable haben, sollten wir uns nicht verwirren lassen. Das Vorgehen bleibt das gleiche! Wieder ist es hilfreich, zuerst so umzuformen, dass wir den konstanten Faktor „minus-sechs“ gut als solchen erkennen können. „eins durch t“ abgeleitet ist „minus eins durch t Quadrat“. Du erinnerst dich vielleicht: Für die Ableitung nutzen wir, dass wir den Bruch auch so schreiben können. Jetzt wieder zusammenfassen – Achtung, Minus mal Minus wird dabei zu Plus – und fertig! Was müssen wir uns also merken? Die Faktorregel kommt zum Einsatz, wenn wir eine Funktion ableiten möchten, bei der vor dem Term, der x enthält, ein konstanter Faktor – also eine Zahl – steht. Beim Ableiten bleibt der Faktor k dann einfach stehen und wir müssen nur den x-Term ableiten. In der Praxis heißt das manchmal, dass wir einen Bruch noch in ein Produkt mit einem konstanten Faktor umwandeln müssen. Außerdem kann man die Faktoren nach dem Ableiten fast immer noch zusammenfassen. Mit ein bisschen Übung haben wir dann auch diese Ableitungstechnik in unserem Repertoire. Exzellent! Eine weitere Sprosse auf der Karriereleiter zum Ableitungsprofi ist erklommen! Die Menge ist begeistert!
Faktorregel bei Ableitungen Übung
-
Beschreibe die Faktorregel.
TippsDie Faktorregel besagt, dass ein konstanter Faktor vor der Potenz von $x$ beim Ableiten einfach erhalten bleibt.
Die Faktorregel hat ihren Namen daher, dass sie das Verhalten eines Faktors im Funktionsterm beim Ableiten beschreibt.
LösungDie Faktorregel können wir beim Ableiten verwenden:
Wenn wir eine Funktion ableiten wollen, die sich aus einem Term $u(x)$, der ein $x$ enthält, und einem beliebigen konstanten Faktor $k$ zusammensetzt, dann bleibt dieser Faktor beim Ableiten erhalten und wir müssen nur den Term ableiten, der das $x$ enthält.Wir schreiben:
$f(x)= k \cdot u(x) \quad f'(x) = k \cdot u'(x)$
Die Faktorregel besagt also, dass ein konstanter Faktor vor einer Potenz von $x$ beim Ableiten erhalten bleibt.
Beispiel:
$f(x) = 4 \cdot x^5 \quad f'(x)=4 \cdot 5x^4 = 20x^4$Hierbei ist $4$ der Faktor und $x^5$ der Term $u(x)$, der $x$ enthält.
-
Vervollständige die Ableitungen.
TippsAllgemein gilt:
$f(x)= k \cdot u(x) \quad f'(x) = k \cdot u'(x) \quad\quad$ (Faktorregel)
Beispiel:
$f(x) = 4 \cdot x^5 \quad f'(x)=4 \cdot 5x^4 = 20x^4$LösungIst ein Funktionsterm das Produkt aus einem konstanten Faktor $k$ und einer Potenz von $x$, so können wir den Faktor beibehalten und die Potenz wie gewohnt ableiten. Es gilt:
$f(x)= k \cdot u(x) \qquad f'(x) = k \cdot u'(x)\quad\quad$ (Faktorregel)Wir wenden diese Regel auf die gegebenen Funktionen an und berechnen:
Beispiel 1:
$f(x)=5x^3 \quad \rightarrow \quad f'(x)=5 \cdot 3x^2 = 15x^2$
Wir haben hierbei die Ableitungsregel für Potenzen angewendet und zum Schluss die beiden Faktoren $5$ und $3$ multipliziert.Beispiel 2:
$f(x)=3x^7 \quad \rightarrow \quad f'(x)=3 \cdot 7x^6 = 21x^6$
Auch hier haben wir die Ableitungsregel für Potenzen angewendet und zum Schluss die beiden Faktoren multipliziert.Beispiel 3:
$f(x)=\frac{x^4}{2} = \frac{1}{2} \cdot x^4 \quad \rightarrow \quad f'(x)=\frac{1}{2} \cdot 4x^3 = \frac{4}{2}x^3 = 2x^3$
Um hier die Faktorregel einfach anwenden zu können, ist es sinnvoll, den Term zunächst als Produkt zu schreiben. Dann können wir beim Ableiten den Faktor $\frac{1}{2}$ beibehalten. Zum Schluss fassen wir zusammen. -
Entscheide, bei welchen Funktionen die Faktorregel beim Ableiten angewendet wird.
TippsEin konstanter Faktor bleibt beim Ableiten erhalten.
Achte darauf, dass es sich um einen konstanten Faktor handeln muss.
Faktor $\cdot$ Faktor = Produkt
LösungFaktorregel:
Wenn wir eine Funktion ableiten wollen, die sich aus einem Term $u(x)$, der die Variable $x$ enthält, und einem beliebigen konstanten Faktor $k$ zusammensetzt, dann bleibt dieser Faktor beim Ableiten erhalten und wir müssen nur den Term ableiten, der das $x$ enthält. Wichtig ist dabei, dass der Faktor konstant ist, er darf also nicht die Variable $x$ enthalten.Bei folgenden Funktionen kann die Faktorregel angewendet werden:
Wir können sie in der Form $k \cdot u(x)$ schreiben.- $f(x) =-\frac{1}{2} \cdot \sqrt{x} \qquad$ Es ist $k = -\frac{1}{2}$ und $u(x) = \sqrt{x}$.
- $f(x) = 1,1 \cdot \sin(x) \qquad$ Es ist $k = 1,1$ und $u(x) = \sin(x)$.
- $f(x) = \frac{2}{x^2} = 2 \cdot \frac{1}{x^2} \qquad$ Es ist $k = 2$ und $u(x) = \frac{1}{x^2}$.
- $f(x) =-4 \frac{2}{x+5} = -4 \cdot 2 \cdot \frac{1}{x+5} = -8 \cdot \frac{1}{x+5} \qquad$ Es ist $k = -8$ und $u(x) = \frac{1}{x+5}$.
- $f(x) = 3x \cdot x^2 \qquad$ Der Faktor enthält die Variable $x$.
- $f(x) = -24 + x^5 \qquad$ Es wird addiert, somit handelt es sich um einen Summanden.
- $f(x) = \frac{x-1}{x+1} \qquad$ Es gibt keinen konstanten Faktor.
- $f(x) = -x \cdot \frac{1}{x^2+2} \qquad$ Der Faktor enthält die Variable $x$.
-
Bestimme die Ableitung der Funktion.
TippsDie Potenzregel besagt: $f(x)=x^n \quad f'(x)=n \cdot x^{n-1}$
Du kannst sie auch auf negative Exponenten und auf Brüche und Dezimalzahlen im Exponenten anwenden.
Du kannst eine Wurzel auch als Exponent schreiben, es gilt:
$\sqrt[n]{x} = x^{\frac{1}{n}}$Beispiel:
$\sqrt[3]{x} = x^{\frac{1}{3}}$LösungWir können die Funktionen ableiten, indem wir die Faktorregel und die Potenzregel anwenden:
- Faktorregel: $f(x)= k \cdot u(x) \quad f'(x) = k \cdot u'(x)$
- Potenzregel: $f(x)=x^n \quad f'(x)=n \cdot x^{n-1}$
Beispiel 1:
$f(x)=-3x^5 \quad \rightarrow \quad f'(x) = -3 \cdot 5x^4 = -15x^4$Beispiel 2:
$f(x)=-\frac{4}{x^2} = -4 \cdot \frac{1}{x^2} = -4 \cdot x^{-2} \quad \rightarrow \quad f'(x) = -4 \cdot -2x^{-3} = 8x^{-3} = \frac{8}{x^3} $Beispiel 3:
$f(x)=2x^{-3} \quad \rightarrow \quad f'(x)= 2 \cdot -3x^{-4} = -6 \cdot x^{-4} = \frac{-6}{x^4}$Beispiel 4:
$f(x)=\frac{-2}{\sqrt{x}} = -2 \cdot \frac{1}{\sqrt{x}} = -2 \cdot \frac{1}{x^{\frac{1}{2}}} = -2 \cdot x^{-\frac{1}{2}} \quad \rightarrow \quad f'(x)= -2 \cdot -\frac{1}{2} x^{-\frac{1}{2}-1} = x^{-\frac{3}{2}}$ -
Bestimme die Ableitung der Funktion $f(x)$ mithilfe der Potenzregel.
TippsDie Potenzregel lautet:
$f(x)=x^n \quad f'(x)=n \cdot x^{n-1}$
Du kannst die Potenzregel auch auf negative Exponenten anwenden.
Beispiel:
$f(x)=x^{-3} \quad f'(x)=-3x^{-4}$
LösungZum Ableiten von Potenzen verwenden wir die Potenzregel. Sie lautet:
$f(x)=x^n \quad f'(x)=n \cdot x^{n-1}$
Wir schreiben beim Ableiten also den Exponenten als Faktor vor die Potenz und verringern den Exponenten der Potenz dann um eins.
Wir wenden diese Regel auf die gegebenen Funktionen an:
- $f(x)=x^3 ~~\quad \rightarrow \quad f'(x)=3 \cdot x^{3-1} = 3x^2$
- $f(x)=x^4 ~~\quad \rightarrow \quad f'(x)=4 \cdot x^{4-1} = 4x^3$
- $f(x)=x^7 ~~\quad \rightarrow \quad f'(x)=7 \cdot x^{7-1} = 7x^6$
- $f(x)=x^{-1} \quad \rightarrow \quad f'(x)=-1 \cdot x^{-1-1} = -x^{-2}$
-
Ermittle den Faktor bei der Ableitung.
TippsSchreibe den Funktionsterm jeweils zuerst so, dass du den konstanten Vorfaktor gut erkennst.
Es gilt:
$f(x)=\sin(x) \quad f'(x)=\cos(x)$
$f(x)=\cos(x) \quad f'(x)=-\sin(x)$$\sqrt{x} = x^{\frac{1}{2}}$
LösungWir können die Funktionen ableiten, indem wir die Faktorregel und die Potenzregel anwenden. Dazu schreiben wir den Funktionsterm zunächst so, dass wir den konstanten Vorfaktor und die Potenz gut erkennen können.
Wir betrachten die einzelnen Funktionen und rechnen Schritt für Schritt:Funktion 1:
$f(x)=3 \frac{4}{\sqrt{x}} = 3 \cdot 4 \cdot \frac{1}{\sqrt{x}} = 12 \cdot x^{-\frac{1}{2}}$
$f'(x)=12 \cdot (-\frac{1}{2}) \cdot x^{-\frac{1}{2}-1} = -6 \cdot x^{-\frac{3}{2}} = -6 \cdot \frac{1}{\sqrt{x}^3}$Funktion 2:
$f(x)=-3 \frac{\sin(x)}{4} = -3 \cdot \frac{1}{4} \cdot \sin(x) = -\frac{3}{4} \cdot \sin(x) = -0,75 \cdot \sin(x)$
$f'(x)= -0,75 \cdot \cos(x)$Funktion 3:
$f(x)=3 \frac{4x^2}{x^3} = 3 \cdot 4 \cdot \frac{x^2}{x^3} = 12 \cdot \frac{1}{x} = 12 \cdot x^{-1}$
$f'(x)= 12 \cdot (-1) \cdot x^{-1-1} = -12 \cdot x^{-2} = -12 \cdot \frac{1}{x^2}$Funktion 4:
$f(x) = 6 \cdot \sqrt[3]{x^4} = 6 \cdot x^{\frac{4}{3}}$
$f'(x) = 6 \cdot \frac{4}{3} \cdot x^{\frac{4}{3}-1} = 8 \cdot x^{\frac{1}{3}} = 8 \cdot \sqrt[3]{x}$
7.718
sofaheld-Level
6.601
vorgefertigte
Vokabeln
7.923
Lernvideos
37.087
Übungen
34.324
Arbeitsblätter
24h
Hilfe von Lehrer*
innen

Inhalte für alle Fächer und Klassenstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Primzahlen
- Geometrische Lagebeziehungen
- Rechteck
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Quadrat
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Was Ist Eine Viertelstunde
- Prisma
- Mitternachtsformel
- Grundrechenarten Begriffe
- Dreiecksarten
- Quader
- Satz Des Pythagoras
- Dreieck Grundschule
- Erste Binomische Formel
- Kreis
- Standardabweichung
- Flächeninhalt
- Volumen Kugel
- Zahlen In Worten Schreiben
- Meter
- Orthogonalität
- Schriftlich Multiplizieren
- Brüche Multiplizieren
- Potenzgesetze
- Distributivgesetz
- Flächeninhalt Dreieck
- Rationale Zahlen
- Volumen Berechnen
- Brüche Addieren
- Kongruenz
- Exponentialfunktion
- Scheitelpunktform
- Logarithmus
- Erwartungswert
- Skalarprodukt
- Primfaktorzerlegung
- Quadratische Ergänzung
- Zinseszins
- Geradengleichung Aus Zwei Punkten Bestimmen
- Sinusfunktion


 Du möchtest schneller & einfacher lernen?
Du möchtest schneller & einfacher lernen?


 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen





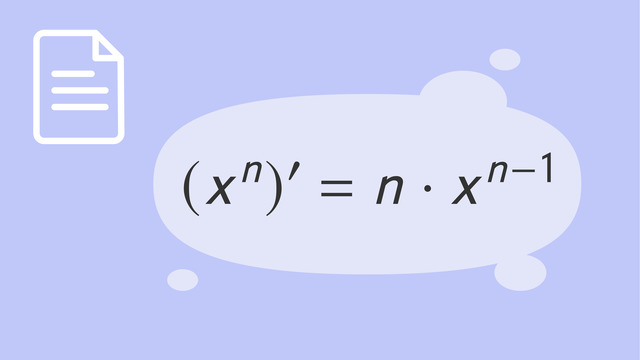









Schön guten Tag, ich habe da mal eine Frage zu dem Video (Faktorregel bei Ableitungen)
Ganz zum Schluss wird die Aufgabe h(t) besprochen.
Meine Frage ist jetzt, wie man am Ende auf t hoch 2 kommt?
Mit freundlichen Grüßen Michelle