Exponentielles Wachstum
Wachstum, Exponentialfunktion, Zerfall, Anfangswert, Wachtsumsfaktor, Ausgleichskurve, GTR, STAT
Beliebteste Videos und Lerntexte
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Was ist exponentielles Wachstum?
- Exponentialfunktionen
- Beispiel „Nachricht“
- Aufstellen der Exponentialfunktion
- Wie weit hat sich die Nachricht nach 10 Tagen in Gruppe A verteilt?
- Wann kennen 400 Menschen die Nachricht in Gruppe B?
- Wann hat sich die Zahl der Menschen, die die Nachricht in Gruppe A kennen, verdoppelt?
- Wann hat sich die Nachricht in beiden Gruppen auf gleich viele Personen verbreitet?
Was ist exponentielles Wachstum?
Schaue dir das folgenden Beispiel an.
Paul erhält $20~€$ Taschengeld. Jedes Jahr wird der Betrag um $2,50~€$ höher. Seine Schwester Camilla bekommt ebenfalls $20~€$ Taschengeld, welches jedes Jahr um $10\%$ erhöht wird.
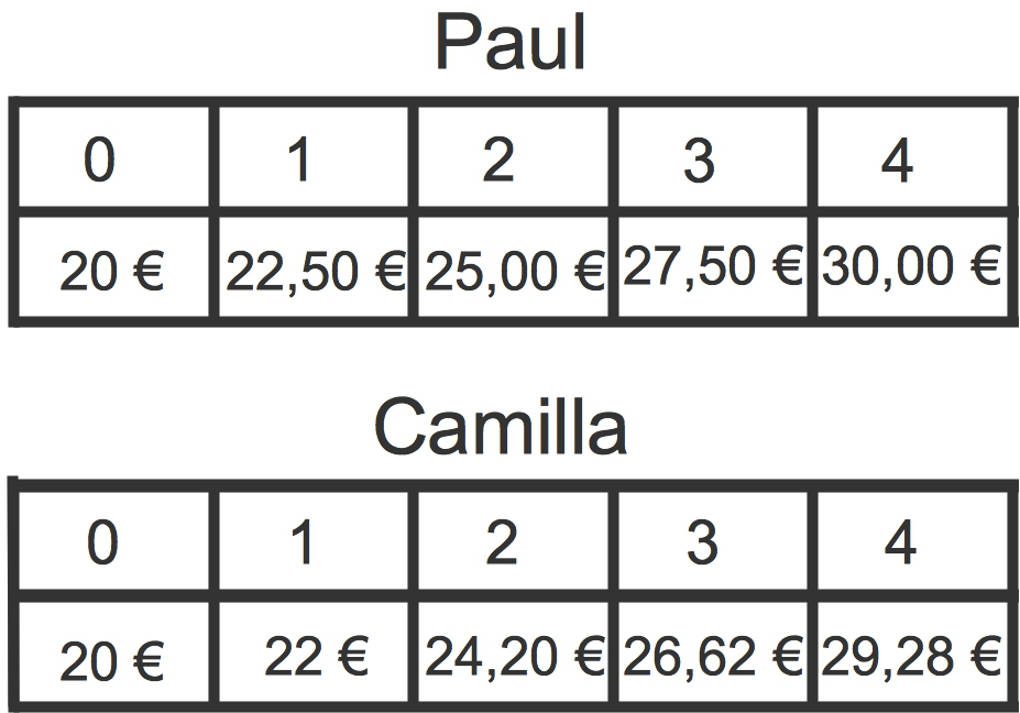
- Das Taschengeld von Paul wächst immer um den gleichen Betrag. Ein solches Wachstum wird als lineares Wachstum bezeichnet.
- Das Taschengeld von Camilla wächst immer um den gleichen Faktor. Ein solches Wachstum wird als exponentielles Wachstum bezeichnet.
Beispiele für exponentielles Wachstum
Schauen wir uns zunächst einige Beispiele für Wachstumsprozesse an:
- Paul legt sein Geld bei einer Bank an. Dafür erhält er Zinsen. Wenn Paul kein Geld abhebt, nimmt das angelegte Geld exponentiell zu. Wie viel Geld dabei herauskommt, berechnest du mit der Zinsrechnung.
- Die Vermehrung von Bakterienkulturen wird häufig exponentiell beschrieben.
- Du erzählst drei Freunden einen Witz. Jeder dieser Freunde, erzählt den Witz wieder drei weiteren Freunden und so weiter. Die Verbreitung des Witzes ist exponentiell.
Um solche Prozesse zu beschreiben, verwendet man Exponentialfunktionen.
Definition
Exponentielles Wachstum, welches auch als unbegrenztes exponentielles Wachstum bezeichnet wird, liegt vor, wenn sich eine Größe in jeweils gleichen Zeitabschnitten (Perioden) immer um denselben Faktor verändert.
Exponentialfunktionen
Eine Exponentialfunktion hat die Funktionsgleichung
$f(x)=c\cdot a^x$.
Dabei ist
- $x$ die unabhängige Variable, diese steht im Exponenten,
- $a\in \mathbb{R}^+$ die Basis der Exponentialfunktion und
- $c\in \mathbb{R}$ eine Konstante. Diese steht für den Anfangswert bei exponentiellen Prozessen.
Der Parameter $a$
Die Basis $a$ der Exponentialfunktion ist
- der Wachstumsfaktor, wenn $a>1$ ist, also bei exponentiellem Wachstum, und
- der Abnahmefaktor, wenn $0 < a < 1$, also bei exponentieller Abnahme.
Beispiel Camilla
Das Taschengeld von Camilla wächst exponentiell. Wir stellen hierzu die zugehörige Exponentialfunktion auf.
- Der Anfangswert ist $20$ [€], das Taschengeld, welches Camilla zu Beginn der Beobachtung, $x=0$, erhält.
- Die Basis $a$ ist der Wachstumsfaktor. Dieser ergibt sich mit der bekannten prozentualen Erhöhung $10\%$ wie folgt
$\quad~~~a=1+\frac{10}{100}=1,1$.
- Damit ist
$\quad~~~f(x)=20\cdot 1,1^x$.
Beispiel „Nachricht“
Eine Nachricht verbreitet sich in zwei Gruppen. Die Verbreitung ist exponentiell:
- In Gruppe $A$ kennen am Anfang $100$ Menschen die Nachricht, nach drei Tagen kennen bereits $152$ Menschen die Nachricht.
- In Gruppe $B$ kennen nach zwei Tagen $145$ Menschen die Nachricht und nach weiteren drei Tagen $193$ Menschen.
Aufstellen der Exponentialfunktion
Zunächst stellen wir die zugehörigen Exponentialfunktion in Abhängigkeit der Variablen $x$, in Tagen, auf.
Bei Gruppe $A$ kennen wir bereits den Anfangswert $c=100$ sowie die Anzahl nach drei Tagen, also $f(3)=152$. Es gilt
$152=100\cdot a^3$.
Wir dividieren durch $100$ und ziehen dann die dritte Wurzel: $a=\sqrt[3]{1,52}\approx 1,15$. Damit lautet die Exponentialfunktion, welche das Verbreiten der Nachricht in Gruppe $A$ beschreibt,
$f(x)=100\cdot 1,15^x$.
Ebenso kann die Exponentialfunktion für die Gruppe $B$ bestimmt werden:
- $g(2)=145$, dies führt zu $145=c\cdot a^2$.
- $g(5)=193$, dies führt zu $193=c\cdot a^5$.
Die obere Gleichung wird nach $c$ umgeformt. Hierfür wird durch $a^2$ dividiert:
$c=\frac{145}{a^2}$.
Dieses $c$ wird in der unteren Gleichung eingesetzt:
$193=\frac{145}{a^2}\cdot a^5=145\cdot a^3$.
Nun wird durch $145$ dividiert und die dritte Wurzel gezogen: $a=\sqrt[3]{1,33}\approx1,1$. Damit kann auch $c$ berechnet werden:
$c=\frac{145}{1,1^2}\approx 120$.
Damit lautet die Exponentialfunktion, welche das Verbreiten der Nachricht in Gruppe $B$ beschreibt
$g(x)=120\cdot 1,1^x$.
Wie weit hat sich die Nachricht nach 10 Tagen in Gruppe A verteilt?
Wenn du wissen möchtest, wie weit sich die Nachricht nach einer gegebenen Zeit verbreitet hat, setzt du diese Zeitangabe in der entsprechenden Funktionsgleichung ein:
$f(10)=100\cdot 1,15^{10}=404,55...$.
Das bedeutet, dass nach 10 Tagen bereits $405$ Menschen die Nachricht kennen.
Wann kennen 400 Menschen die Nachricht in Gruppe B?
Du kannst auch nach der Zeit fragen. Dieses Mal ist der Funktionswert gegeben: $400=120\cdot 1,1^x$. Zuerst dividierst du durch $120$ und erhältst die Gleichung
$1,1^x=\frac{10}3$.
Eine solche Gleichung löst du mit Logarithmen:
$x=\frac{\ln\left(\frac{10}3\right)}{\ln(1,1)}=12,63...$.
Nach ungefähr 13 Tagen hat sich die Nachricht auf $400$ Personen verbreitet.
Wann hat sich die Zahl der Menschen, die die Nachricht in Gruppe A kennen, verdoppelt?
Du löst die Gleichung $g(x)=240$:
$\begin{array}{rclll} 240&=&120\cdot 1,1^x&|&:120\\ 2&=&1,1^x&|&\ln(~~~)\\ x&=&\frac{\ln(2)}{\ln(1,1)}\\ x&=&7,27... \end{array}$
Nach etwas mehr als sieben Tagen hat sich die Nachricht in Gruppe $A$ auf die doppelte Anzahl an Menschen verbreitet. Diese Zeit wird als Verdoppelungszeit oder auch Generationenzeit bezeichnet.
Bei exponentieller Abnahme wird oftmals nach der Zeit gefragt, nach welcher ein Bestand sich halbiert hat. Diese Zeit wird als Halbwertzeit bezeichnet.
Wann hat sich die Nachricht in beiden Gruppen auf gleich viele Personen verbreitet?
Dieses Mal ist der Schnittpunkt zweier Funktionen gesucht: $f(x)=g(x)$.
Diese Gleichung wird nun umgeformt.
$\begin{array}{crclll} &100\cdot 1,15^x&=&120\cdot 1,1^x&|&:100\\ \Leftrightarrow&1,15^x&=&1,2\cdot 1,1^x&|&:1,1^x\\ \Leftrightarrow&\left(\frac{1,15}{1,1}\right)^x&=&1,2&|&\ln(~~~)\\ &x&=&\frac{\ln(1,2)}{\ln\left(\frac{1,15}{1,1}\right)}\\ &&=&4,10 \end{array}$
Nach ungefähr vier Tagen ist das Gerücht in beiden Gruppen gleichermaßen verbreitet.
Alle Videos und Lerntexte zum Thema
Videos und Lerntexte zum Thema
Exponentielles Wachstum (4 Videos, 1 Lerntext)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Exponentielles Wachstum (3 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Primzahlen
- Geometrische Lagebeziehungen
- Rechteck
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Quadrat
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Was Ist Eine Viertelstunde
- Prisma
- Mitternachtsformel
- Grundrechenarten Begriffe
- Dreiecksarten
- Quader
- Satz Des Pythagoras
- Dreieck Grundschule
- Erste Binomische Formel
- Kreis
- Standardabweichung
- Flächeninhalt
- Volumen Kugel
- Zahlen In Worten Schreiben
- Meter
- Orthogonalität
- Schriftlich Multiplizieren
- Brüche Multiplizieren
- Potenzgesetze
- Distributivgesetz
- Flächeninhalt Dreieck
- Rationale Zahlen
- Volumen Berechnen
- Brüche Addieren
- Kongruenz
- Exponentialfunktion
- Scheitelpunktform
- Logarithmus
- Erwartungswert
- Skalarprodukt
- Primfaktorzerlegung
- Quadratische Ergänzung
- Zinseszins
- Geradengleichung Aus Zwei Punkten Bestimmen
- Sinusfunktion







 Exponentielles Wachstum – Zinseszins
Exponentielles Wachstum – Zinseszins
 Exponentielle Wachstumsvorgänge
Exponentielle Wachstumsvorgänge
 Exponentielle Wachstumsvorgänge – Modellierung
Exponentielle Wachstumsvorgänge – Modellierung









