Erwartungswert einer Zufallsvariable
faires Spiel, Mittelwert, arithmetisches Mittel, durchschnittlich, Lageparameter, mittlere quadratische Abweichung, Streuungsparameter, Erwartungswert
Beliebteste Videos
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Was ist der Erwartungswert?
- Der Erwartungswert bei Spielen
- Der Erwartungswert bei binomialverteilten Zufallsgrößen
Was ist der Erwartungswert?
Um zu verstehen, was ein Erwartungswert ist, wäre ist hilfreich, wenn du dich schon ein bisschen mit der folgenden Schreibweise auskennst. Wir betrachten ein Zufallsexperiment mit der Ergebnismenge
$\Omega=\{e_1,e_2,\dots,e_n\}$
und den Wahrscheinlichkeiten $p_i=P(e_i)$ für $i=1,\dots,n$.
Zusätzlich sei die Zufallsvariable oder auch Zufallsgröße $X$ gegeben, welche jedem Ergebnis der Ergebnismenge eine Zahl zuordnet:
$X:\begin{array}{lcr} \Omega&\rightarrow&\mathbb{R}\\ e_i&\rightarrow&x_i \end{array}$
Der Erwartungswert $E(X)$ (oder auch $\mu$) dieser Zufallsgröße ist wie folgt definiert:
$E(X)=\mu=\sum\limits_{i=1}^nx_i\cdot P(X=x_i)$.
Dabei sind $x_1$, ..., $x_n$ die möglichen Ausprägungen der Zufallsgröße und $P(X=x_i)=P(e_i)$ ist die Wahrscheinlichkeit für das Eintreten der Ausprägung $x_i$.
Genau wie das arithmetische Mittel ist der Erwartungswert ein Lageparameter.
Das Glücksrad
Dieses Glücksrad wird einmal gedreht. (Hinweis: Glücksräder machen nicht glücklich.)
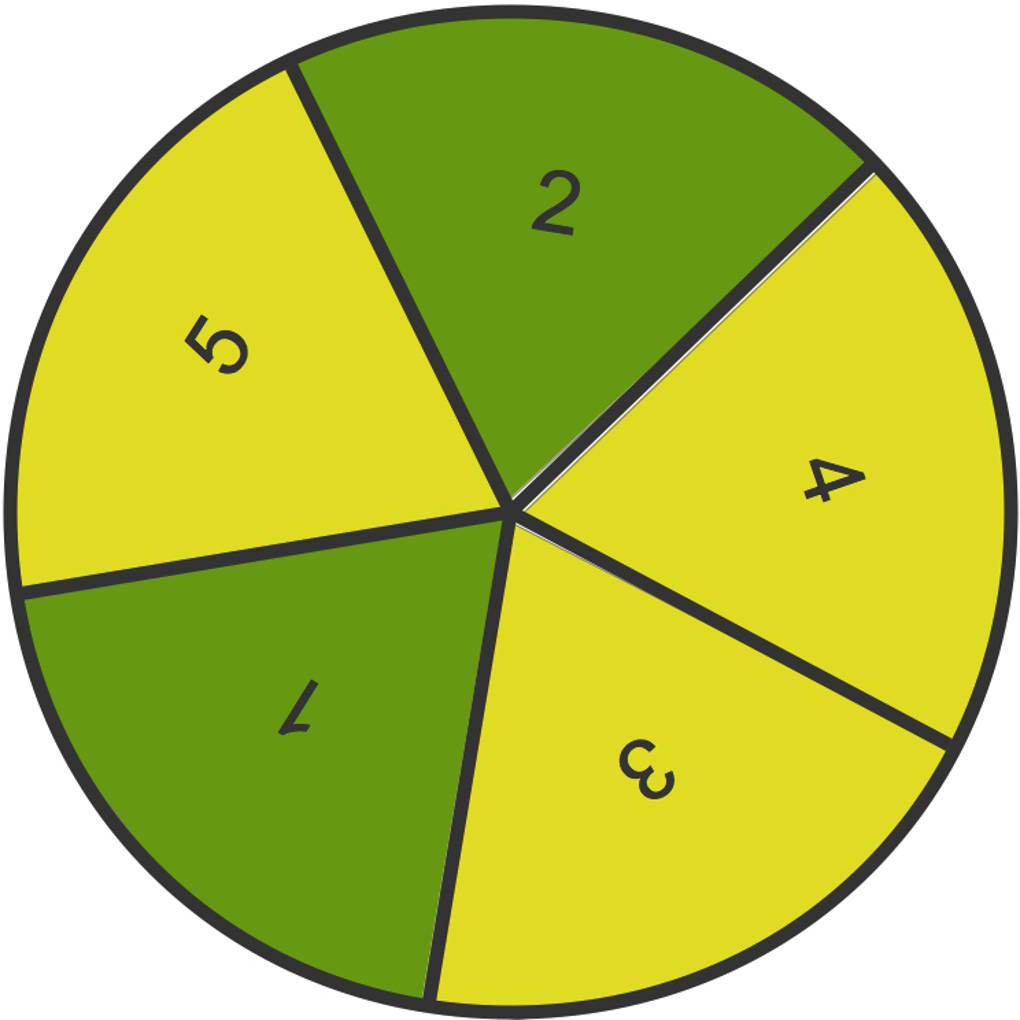
Die Zufallsgröße $X$ ordnet den ungeraden Zahlen $1$, $3$, $5$ die Zahl $10$ und den geraden $2$, $4$ die Zahl $20$ zu.
$P(X=10)=P( \{ 1,3,5 \} )=\frac35$
$P(X=20)=P( \{ 2,4 \} )=\frac25$
Damit kann der Erwartungswert berechnet werden:
$E(X)=\mu=\frac35\cdot 10+\frac25\cdot 20=6+8=14$.
Du wirst vielleicht sagen: „$14$?! Das ergibt doch keinen Sinn!“ Der Wert $14$ ergibt tatsächlich erst Sinn, wenn wir das Zufallsexperiment sehr häufig durchführen. Dann werden wir im Schnitt eine $14$ gedreht haben.
Der Erwartungswert bei Spielen
Ein faires Spiel?
Paul hat sich auf folgendes Spiel eingelassen: Er setzt $2~€$ und darf das Glücksrad einmal drehen. Es kommt zu den folgenden Auszahlungen:
- Bei einem roten Feld erhält er $1~€$,
- bei einem grünen Feld $1,50~€$
- und bei einem blauen Feld $4~€$.
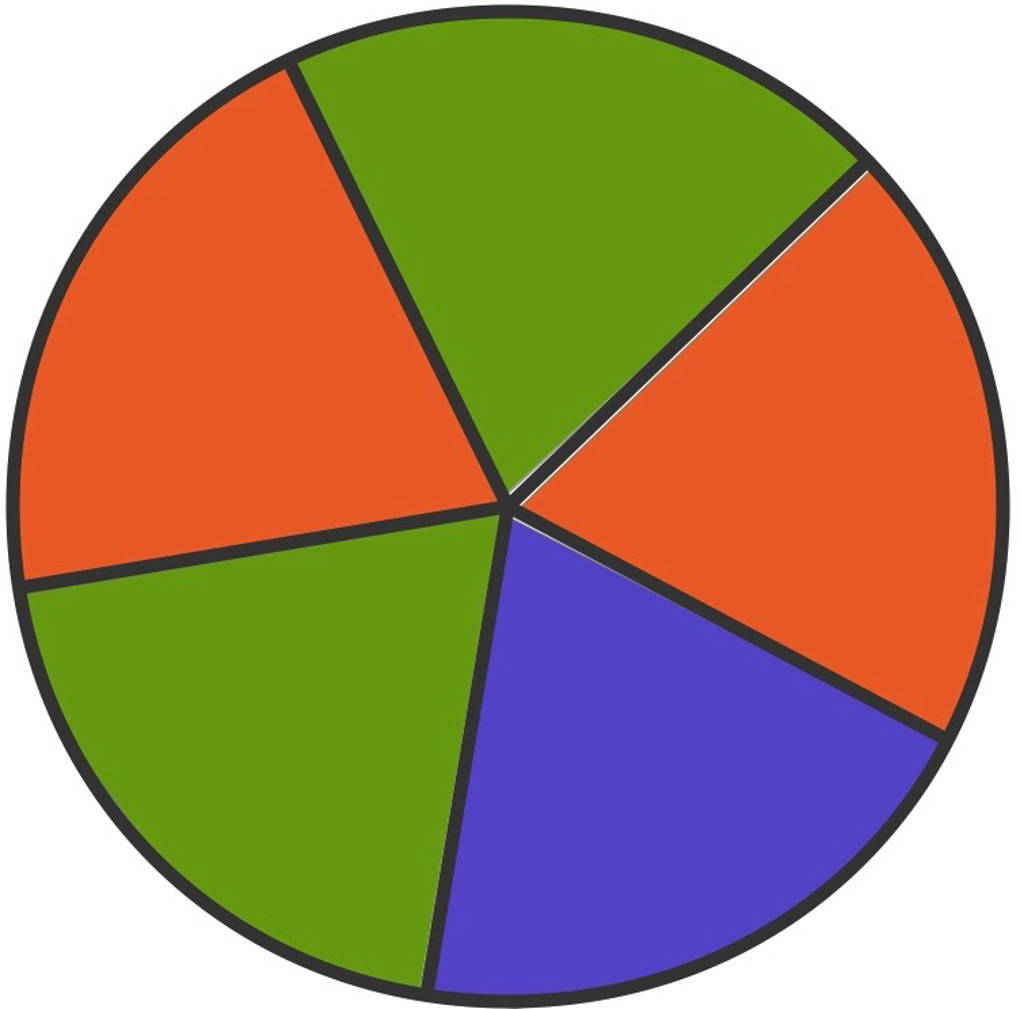
Nun fragt sich Paul: Ist dieses Spiel auf lange Sicht fair?
Aber was versteht man unter einem fairen Spiel? Ein Spiel heißt fair, wenn es auf lange Sicht sowohl für den Spieler als auch für den Anbieter des Spiels gleich ausgeht. Sowohl der Anbieter als auch der Spieler verliert weder auf lange Sicht, noch gewinnt einer von beiden.
Schauen wir uns die Bedingungen genauer an:
- Die Ergebnismenge ist $\Omega=\{$rot, grün, blau$\}$.
- Die Wahrscheinlichkeiten der Ergebnisse sind $P($rot$)=P($grün$)=\frac25$ und $P($blau$)=\frac15$.
Zunächst schauen wir uns die Zufallsgröße $X$ an.
$X:\begin{array}{lcr} \text{ rot}&\rightarrow&1,00~€\\ \text{grün}&\rightarrow&1,50~€\\ \text{blau}&\rightarrow&4,00~€ \end{array}$
Nun kannst du den Erwartungswert berechnen.
$E(X)=\frac25\cdot 1~€+\frac25\cdot 1,50~€+\frac15\cdot 4~€=1,80~€$
Weil Paul pro Spiel $2~€$ Einsatz bezahlen muss und er im Schnitt weniger (nämlich $1,80~€$) gewinnt, ist dieses Spiel für ihn nicht fair.
Wann ist ein Spiel fair?
Nun kann man sich natürlich auch fragen, welche Auszahlung $x$ in Euro Paul für das blaue Feld erhalten sollte, damit das Spiel fair ist.
Es muss dann gelten $E(X)=2~€$. Dies führt zu der folgenden Gleichung:
$E(X)=\frac25\cdot 1~€+\frac25\cdot 1,50~€+\frac15\cdot x~€=2~€$.
Diese Gleichung ist äquivalent zu
$1~€+\frac15\cdot x~€=2~€$.
Nun kannst du auf beiden Seiten $1~€$ subtrahieren und dann mit $5$ multiplizieren. Dies führt zu $x=5$.
Also müsste Paul eine Auszahlung von $5~€$ für „blau“ erhalten, damit das Spiel fair ist.
Der Erwartungswert bei binomialverteilten Zufallsgrößen
Eine Münze soll 12-mal geworfen werden.

$X$ sei die Zufallsgröße für die Häufigkeit des Auftretens von „Kopf“. Hier liegt eine Binomialverteilung vor. Der Erwartungswert einer binomialverteilten Zufallsgröße lässt sich wie folgt berechnen:
$E(X)=\mu=n\cdot p=12\cdot \frac12=6$.
Dabei ist $n$ die Länge der Bernoullikette. Die Länge der Bernoullikette sagt aus, wie oft das Experiment durchgeführt wird. Die Wahrscheinlichkeit für das Eintreten von „Kopf“ wird durch $p$ beschrieben.
Bei $12$ Würfen kommt also durchschnittlich $6$ Mal „Kopf“. Wir können auch sagen: Bei $12$ Würfen erwarten wir $6$ Mal „Kopf“. Das ist doch logisch, oder?
Alle Videos zum Thema
Videos zum Thema
Erwartungswert einer Zufallsvariable (2 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Erwartungswert einer Zufallsvariable (2 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Primzahlen
- Geometrische Lagebeziehungen
- Rechteck
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Quadrat
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Was Ist Eine Viertelstunde
- Prisma
- Mitternachtsformel
- Grundrechenarten Begriffe
- Dreiecksarten
- Quader
- Satz Des Pythagoras
- Dreieck Grundschule
- Erste Binomische Formel
- Kreis
- Standardabweichung
- Flächeninhalt
- Volumen Kugel
- Zahlen In Worten Schreiben
- Meter
- Orthogonalität
- Schriftlich Multiplizieren
- Brüche Multiplizieren
- Potenzgesetze
- Distributivgesetz
- Flächeninhalt Dreieck
- Rationale Zahlen
- Volumen Berechnen
- Brüche Addieren
- Kongruenz
- Exponentialfunktion
- Scheitelpunktform
- Logarithmus
- Erwartungswert
- Skalarprodukt
- Primfaktorzerlegung
- Quadratische Ergänzung
- Zinseszins
- Geradengleichung Aus Zwei Punkten Bestimmen
- Sinusfunktion




 Erwartungswert
Erwartungswert
 Erwartungswert – faires Spiel
Erwartungswert – faires Spiel









