Gleichungen 3. Grades und biquadratische Gleichungen
Oft musst du Nullstellen von Funktionen vom Grad 3, also kubischen Funktionen, oder von biquadratischen Funktionen bestimmen. Du musst also entsprechende Gleichungen lösen.
Beliebteste Videos und Lerntexte
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Was ist eine biquadratische Gleichung?
- Wie werden biquadratische Gleichungen gelöst?
- Was ist eine Gleichung 3. Grades?
Was ist eine biquadratische Gleichung?
Wir schauen uns erst einmal an, was eine biquadratische Gleichung ist. Unter einer biquadratischen Gleichung versteht man eine Gleichung der Form
$x^4 + p x^2 + q = 0$
oder, etwas allgemeiner,
$a x^4 + b x^2 + c = 0$.
Dabei muss $a\neq 0$ sein.
Beispiele für biquadratische Gleichungen
- $x^4 - 2x^2 - 3 = 0$
- $0,2x^4 -x^2 + 0,8 = 0$
- $x^4 + 2x^2 = 0$
Alle diesen Gleichungen haben gemeinsam, dass sie
- zum einen den Grad $4$ haben, man nennt solche Gleichungen im allgemeinen quartische Gleichungen, und
- zum anderen nur Potenzen mit geraden Exponenten haben.
Wir schauen uns nun die obere der beiden allgemeinen Darstellungen einer biquadratischen Gleichung an:
$x^4 + p x^2 + q = \left(x^2\right)^2+p\left(x^2\right)+q=0$.
Du siehst, dies ist eine quadratische Gleichung in $x^2$. Daher kommt auch der Name „biquadratisch“. Wenn du $x^2$ durch $z$ ersetzt oder, anders ausgedrückt, substituierst, erhältst du
$z^2 + p z + q = 0$,
also eine quadratische Gleichung in $z$.
Die pq-Formel
Die beiden Formen der biquadratischen Gleichungen könnten dich an quadratische Gleichungen
$x^2+px+q=0$
oder
$ax^2+bx+c=0$
erinnern. Weißt du noch, wie du solche Gleichungen löst? Richtig, mit der pq-Formel.
Angewendet auf die obere der beiden Gleichungen $x^2+px+q=0$ in Normalform lautet diese:
$x_{1,2}=-\frac p2\pm\sqrt{\left(\frac p2\right)^2-q}$.
Wie werden biquadratische Gleichungen gelöst?
Dies schauen wir uns an den obigen Beispielen für biquadratische Gleichungen an.
Beispiel 1
Es soll die Gleichung $x^4 - 2x^2 - 3 = 0$ gelöst werden. Die Lösungen dieser Gleichung sind die Nullstellen der biquadratischen Funktion $f(x)=x^4 - 2x^2 - 3$, deren Funktionsgraph du hier sehen kannst.
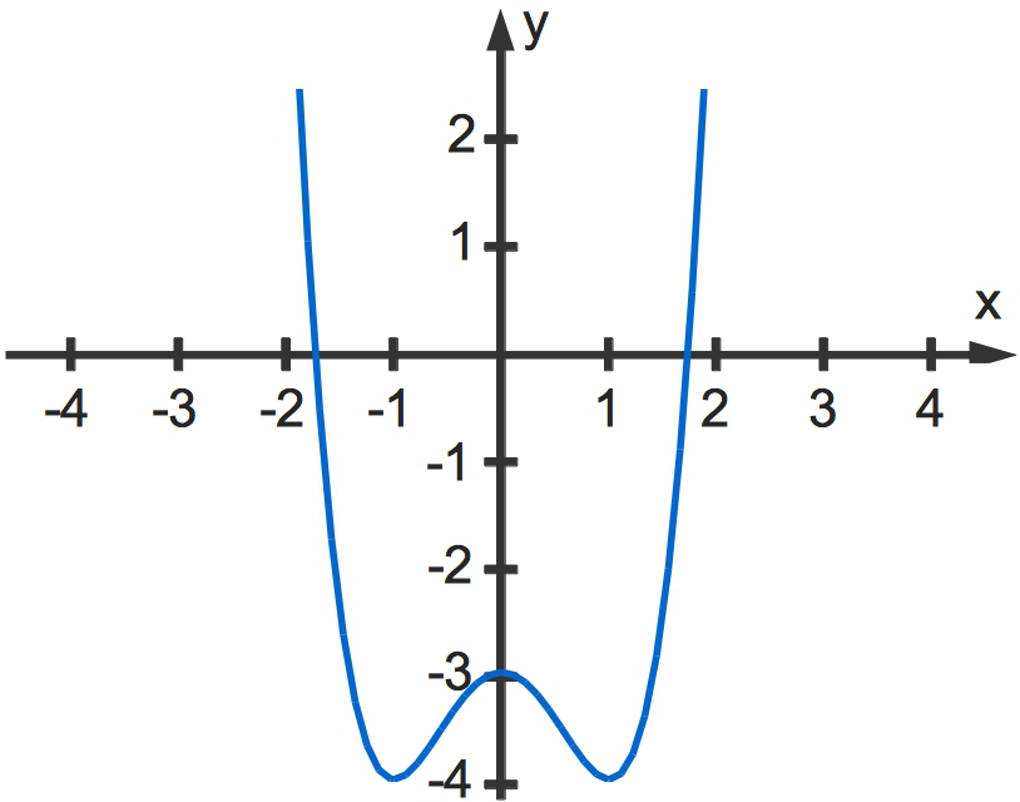
- Substituiere $x^2$ durch $z$. So erhältst du $z^2-2z-3=0$.
- Nun löst du diese Gleichung mit Hilfe der pq-Formel:
$\qquad\begin{array}{rcl} z_{1,2}&=&-\frac {-2}2\pm\sqrt{\left(\frac {-2}2\right)^2+3}\\ &=&1\pm\sqrt 4\\ z_1&=&1+2=3\\ z_2&=&1-2=-1 \end{array}$
- Beachte: Du möchtest die Lösungen für $x$ finden. Das bedeutet, dass du resubstituieren musst:
- $x^2=z_1=3$, also $x=\pm\sqrt 3$ oder
- $x^2=z_2=-1$: Diese Gleichung ist im Bereich der reellen Zahlen nicht lösbar.
Die Lösungsmenge der Gleichung $x^4 - 2x^2 - 3 = 0$ ist somit $\mathbb{L}=\left\{\pm\sqrt 3\right\}$.
Beispiel 2
Gesucht sind die Nullstellen der biquadratischen Funktion $f(x)=0,2x^4 -x^2 + 0,8$.
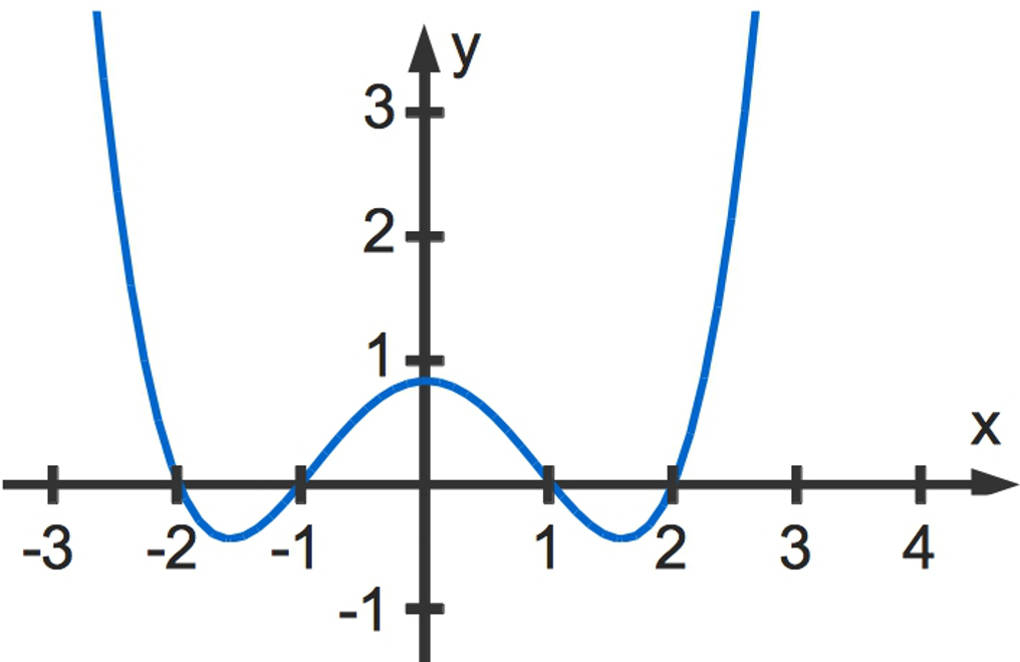
Du löst also die Gleichung $0,2x^4 -x^2 + 0,8=0$ und gehst so vor wie bei dem vorigen Beispiel.
- Substitution von $x^2=z$ führt zu $0,2z^2 -z + 0,8=0$.
- Multipliziere mit $5$, um die Gleichung in Normalform zu überführen. Die Gleichung lautet nun $z^2 -5z +4=0$. Nun kannst du die pq-Formel anwenden.
$\qquad\begin{array}{rcl} z_{1,2}&=&-\frac {-5}2\pm\sqrt{\left(\frac {-5}2\right)^2-4}\\ &=&2,5\pm\sqrt{2,25}\\ z_1&=&2,5+1,5=4\\ z_2&=&2,5-1,5=1 \end{array}$
Resubstituiere nun:
- $x^2=z_1=4$. Du ziehst die Wurzel und erhältst $x=\pm 2$.
- $x^2=z_2=1$. Wieder ziehst du die Wurzel und erhältst $x=\pm 1$.
Die Nullstellen der obigen Funktion sind $\pm2$ sowie $\pm1$. Dies kannst du auch gut an dem Funktionsgraphen erkennen.
Beispiel 3
Die biquadratische Gleichung $x^4 + 2x^2 = 0$ kannst du durch Ausklammern von $x^2$ lösen: $x^2(x^2+2)=0$. Du verwendest die Tatsache, dass ein Produkt $0$ ist, wenn einer der Faktoren $0$ ist. Also ist
- entweder $x^2=0$, also $x=0$, oder
- $x^2+2=0$. Diese Gleichung besitzt keine Lösung im Bereich der reellen Zahlen.
Die Lösungsmenge der obigen Gleichung ist $\mathbb{L}=\left\{0\right\}$.
Hier siehst du den Graphen der Funktion $f(x)=x^4 + 2x^2$.
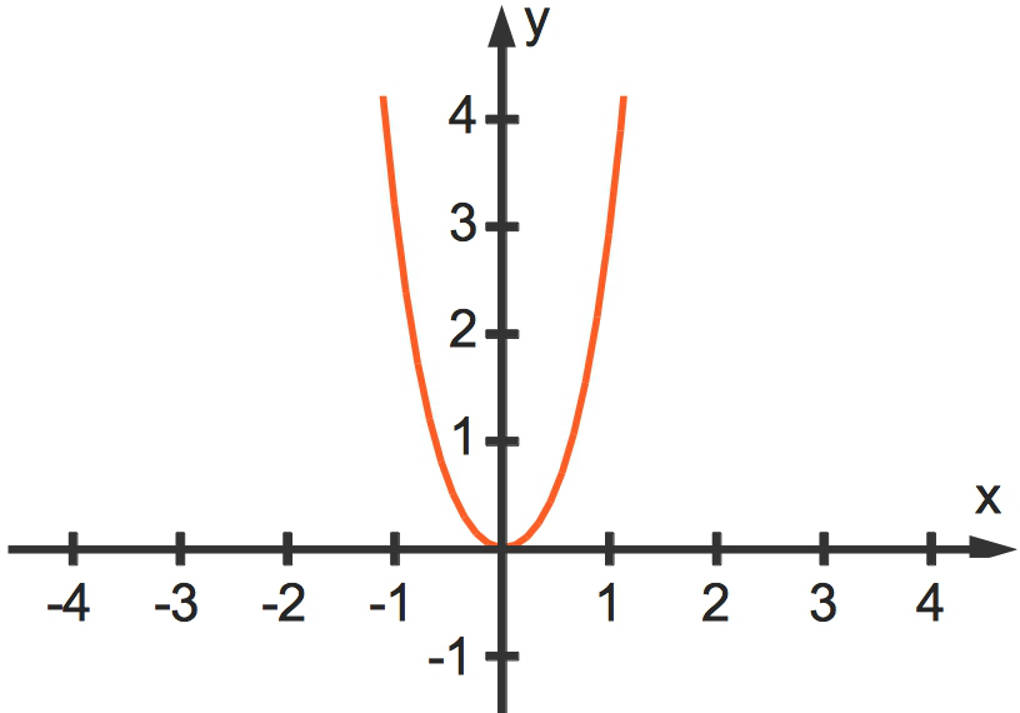
Du kannst an den Beispielen bereits erkennen, dass eine biquadratische Gleichung zwei oder vier oder eine Lösung haben kann. Darüber hinaus kann eine biquadratische Gleichung auch keine oder auch drei Lösungen haben.
Was ist eine Gleichung 3. Grades?
In einer Gleichung 3. Grades ist der höchste Exponent die $3$. Man nennt solche Gleichungen auch kubisch.
$ax^3+bx^2+cx+d=0$
Es muss $a\neq 0$ gelten. Solche Gleichungen erhältst du zum Beispiel, wenn du die Nullstellen einer kubischen Funktion bestimmen sollst.
Mögliche Lösungsverfahren für kubische Gleichungen
- Wenn $d=0$ ist, lautet die Gleichung $ax^3+bx^2+cx=0$. In diesem Fall kannst du $x$ ausklammern: $x(ax^2+bx+c)=0$. Damit ist eine Nullstelle gegeben durch $x=0$. Die anderen, falls weitere Nullstellen existieren, erhältst du durch die Lösung der quadratischen Gleichung mit Hilfe der pq-Formel.
- Wenn $b=c=0$ ist, lautet die Gleichung $ax^3+d=0$. Diese Gleichung kann nach x umgestellt werden. Du erhältst:
$\quad x=-\sqrt[3]{\frac da}$.
- Sehr schön ist es, wenn du eine kubische Gleichung in faktorisierter Form, zum Beispiel $(x+1)(x-1)(x+3)=0$, vorliegen hast. Dann kannst du die Lösungen ablesen. Jeder einzelne Faktor kann $0$ sein. In diesem Beispiel sind die Lösungen, $x_1=-1$, $x_2=1$ und $x_3=-3$.
In allen übrigen Fällen hilft dir die Polynomdivision weiter.
Hierfür schauen wir uns nun ein Beispiel an.
Beispiel
Du sollst die Nullstellen der Funktion $f(x)=x^3-3x^2+4$ finden. Den Funktionsgraphen kannst du hier sehen.
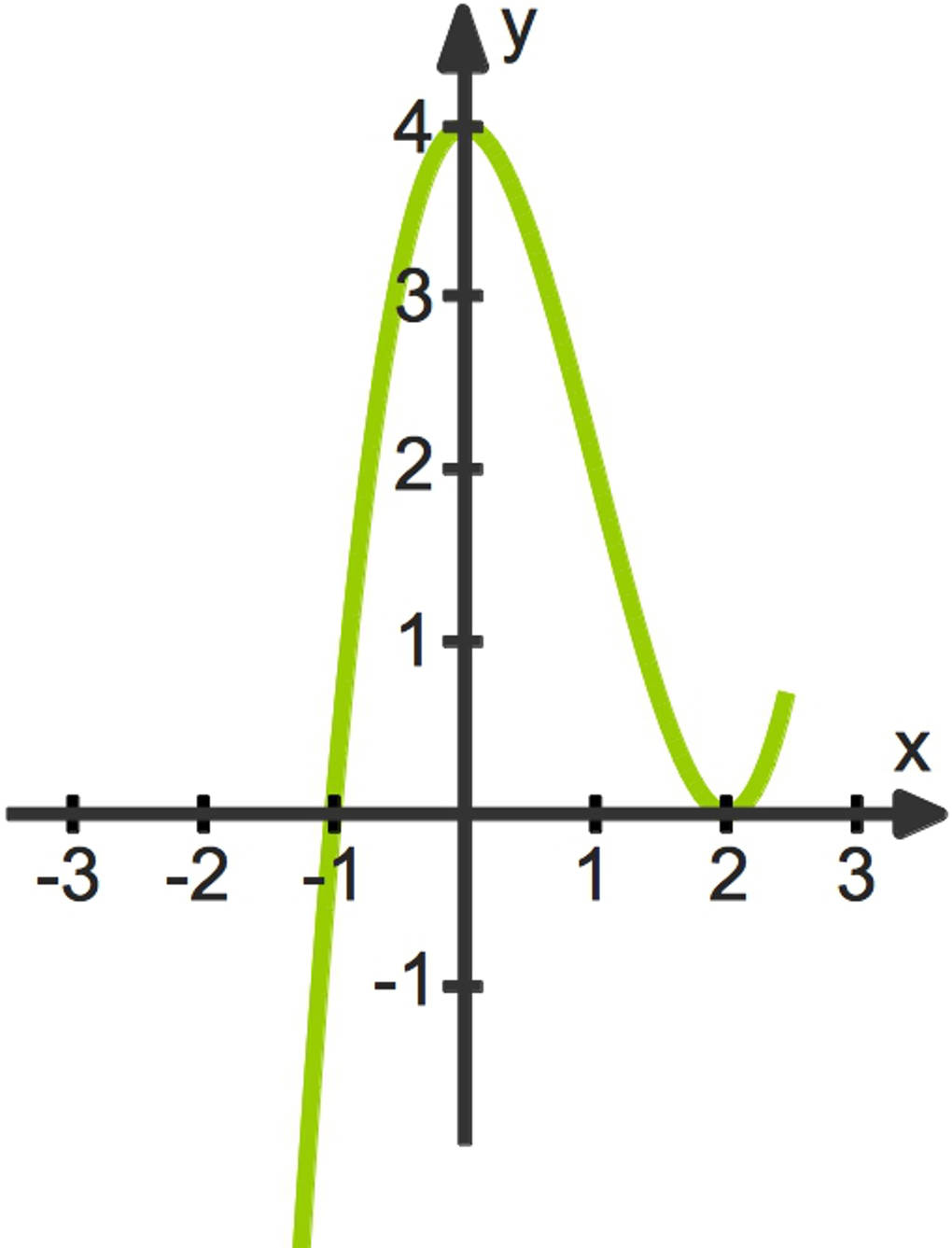
Wir setzen voraus, dass eine Nullstelle bereits bekannt ist, zum Beispiel $x_1=2$. Wenn dem nicht so ist, musst du durch Einsetzen in die Funktionsgleichung eine Nullstelle finden. Dies funktioniert jedoch nur, wenn die Funktion eine ganzzahlige Nullstelle hat, die zusätzlich nicht so sehr groß ist.
Nun dividierst du den Funktionsterm durch $x$ minus die bekannte Nullstelle: $(x^3-3x^2+4):(x-2)$. Hier führst du eine Polynomdivision durch. Das Ergebnis dieser Polynomdivision lautet: $(x^2-x-2)$.
Somit gilt:
$x^3-3x^2+4=(x-2)(x^2-x-2)$
Du kannst also den kubischen Funktionsterm als Produkt zweier Faktoren schreiben:
$f(x)=x^3-3x^2+4=(x-2)(x^2-x-2)$.
Die weiteren Nullstellen der Funktion findest du, sofern vorhanden, durch Lösen der Gleichung $x^2-x-2=0$. Auch hier verwendest du die pq-Formel.
$\begin{array}{rcl} x_{1,2} &=& -\frac{-1}{2} \pm \sqrt{\left( \frac{-1}{2} \right)^2 + 2}\\ &=& 0,5 \pm \sqrt{2,25}\\ x_1 &=& 0,5+1,5=2\\ x_2 &=& 0,5-1,5=-1 \end{array}$
Du siehst, dass eine Nullstelle, nämlich $2$, zweimal vorkommt. Eine solche Nullstelle wird als doppelte Nullstelle bezeichnet. Eine doppelte Nullstelle ist immer ein lokaler Tief- oder Hochpunkt.
Die Nullstellen der obigen Funktion $f(x)=x^3-3x^2+4$ sind somit $-1$ und $2$. Dies kannst du ja auch an dem Funktionsgraphen erkennen.
Übrigens: Eine kubische Gleichung kann eine Lösung oder zwei oder drei Lösungen besitzen. Keine Lösung ist nicht möglich.
Alle Videos und Lerntexte zum Thema
Videos und Lerntexte zum Thema
Gleichungen 3. Grades und biquadratische Gleichungen (2 Videos, 1 Lerntext)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Gleichungen 3. Grades und biquadratische Gleichungen (3 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Primzahlen
- Geometrische Lagebeziehungen
- Rechteck
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Quadrat
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Was Ist Eine Viertelstunde
- Prisma
- Mitternachtsformel
- Grundrechenarten Begriffe
- Dreiecksarten
- Quader
- Satz Des Pythagoras
- Dreieck Grundschule
- Erste Binomische Formel
- Kreis
- Standardabweichung
- Flächeninhalt
- Volumen Kugel
- Zahlen In Worten Schreiben
- Meter
- Orthogonalität
- Schriftlich Multiplizieren
- Brüche Multiplizieren
- Potenzgesetze
- Distributivgesetz
- Flächeninhalt Dreieck
- Rationale Zahlen
- Volumen Berechnen
- Brüche Addieren
- Kongruenz
- Exponentialfunktion
- Scheitelpunktform
- Logarithmus
- Erwartungswert
- Skalarprodukt
- Primfaktorzerlegung
- Quadratische Ergänzung
- Zinseszins
- Geradengleichung Aus Zwei Punkten Bestimmen
- Sinusfunktion





 Gleichungen 3. Grades ohne Absolutglied – Ausklammern
Gleichungen 3. Grades ohne Absolutglied – Ausklammern
 Gleichungen 3. Grades lösen – Polynomdivision
Gleichungen 3. Grades lösen – Polynomdivision
 Biquadratische Gleichungen
Biquadratische Gleichungen









