Bestimmte Integrale und Flächen mit Integralen berechnen
Zu Funktionen gehören Kurvendiskussionen: Du musst schließlich einen Funktionsgraphen zeichnen. Ganz oft folgt darauf eine Integrationsaufgabe. Was das bedeutet, erfährst du hier.
Beliebteste Videos
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Flächenberechnung
- Flächen zwischen Funktionsgraphen und $x$-Achse
- Der Funktionsgraph liegt komplett oberhalb der $x$-Achse
- Der Funktionsgraph liegt komplett unterhalb der $x$-Achse
- Der Funktionsgraph hat Nullstellen auf dem Intervall
- Flächen zwischen Funktionsgraphen
- Variationen der Aufgabenstellung
Flächenberechnung
Das Berechnen von Flächeninhalten ist ein zentraler Punkt in der Analysis. Dabei geht es darum Inhalte von Flächen zu berechnen, die entweder von dem Graphen einer Funktion sowie der $x$-Achse oder aber von zwei Funktionsgraphen eingeschlossen werden.
Was benötigst du hierfür?
- Du kennst eine Funktion $f$ sowie deren Funktionsgleichung oder auch zwei Funktionen $f$ und $g$, je nach Aufgabenstellung.
- Du musst zu den betreffenden Funktionen eine Stammfunktion oder allgemeiner das unbestimmte Integral ermitteln.
- Schließlich benötigst du noch Grenzen für die Fläche.
Du verwendest nun den Haupsatz der Differential- und Integralrechnung: Dieser beschreibt, wie du das bestimmte Integral bei gegebenen Integrationsgrenzen berechnen kannst.
$\int\limits_a^b~f(x)~dx=\left[F(x)\right]_a^b=F(b)-F(a)$
Dabei ist $F$ eine Stammfunktion von $f$, das heißt $F'(x)=f(x)$.
Doch gibt das bestimmte Integral immer einen Flächeninhalt an? Nein! Du musst verschiedene Fälle unterscheiden.
Flächen zwischen Funktionsgraphen und $x$-Achse
Wir betrachten zunächst den Fall von Flächen, welche von dem Graphen einer Funktion sowie der $x$-Achse eingeschlossen werden. Die Integrationsgrenzen können dabei in der Aufgabenstellung vorgegeben oder aber Nullstellen der Funktion sein. Im Folgenden betrachten wir jeweils ein Intervall $I=[a;b]$. $a$ und $b$ sind dann die untere sowie obere Integrationsgrenze.
Der Funktionsgraph liegt komplett oberhalb der $x$-Achse
Schau dir hierfür ein Beispiel an:
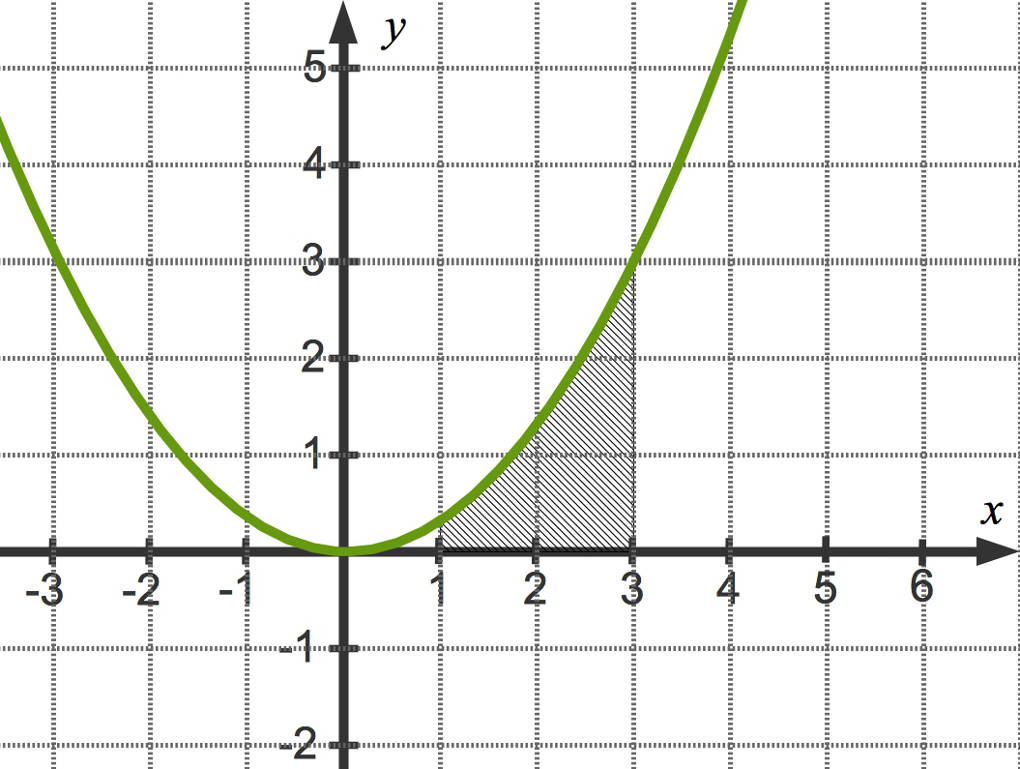
Der Funktionsgraph der Funktion $f$ mit $f(x)=\frac13x^{2}$ schließt mit der $x$-Achse über dem Intervall $I=[1;3]$ das schraffierte Flächenstück ein. Dieses liegt komplett oberhalb der $x$-Achse. In diesem Fall gibt das bestimmte Integral folgenden Flächeninhalt an:
$A=\int\limits_1^3~\frac13x^2~dx=\left[\frac19x^3\right]_1^3=\frac193^3-\frac191^3=\frac{26}9$.
Der Funktionsgraph liegt komplett unterhalb der $x$-Achse
Der Fall, dass das Flächenstück komplett unterhalb der $x$-Achse liegt, ist sehr ähnlich zu dem obigen. Da Flächeninhalte sicher nicht negativ sein können, gehst du ebenso vor wie in dem vorherigen Beispiel. Du musst bei dem bestimmten Integral allerdings das Vorzeichen vertauschen. Alternativ kannst du auch den Betrag des bestimmten Integrals bilden.
Der Funktionsgraph hat Nullstellen auf dem Intervall
Etwas komplizierter gestaltet sich die Situation, wenn sich auf dem gegebenen Intervall eine oder mehrere Nullstellen der Funktion befinden:
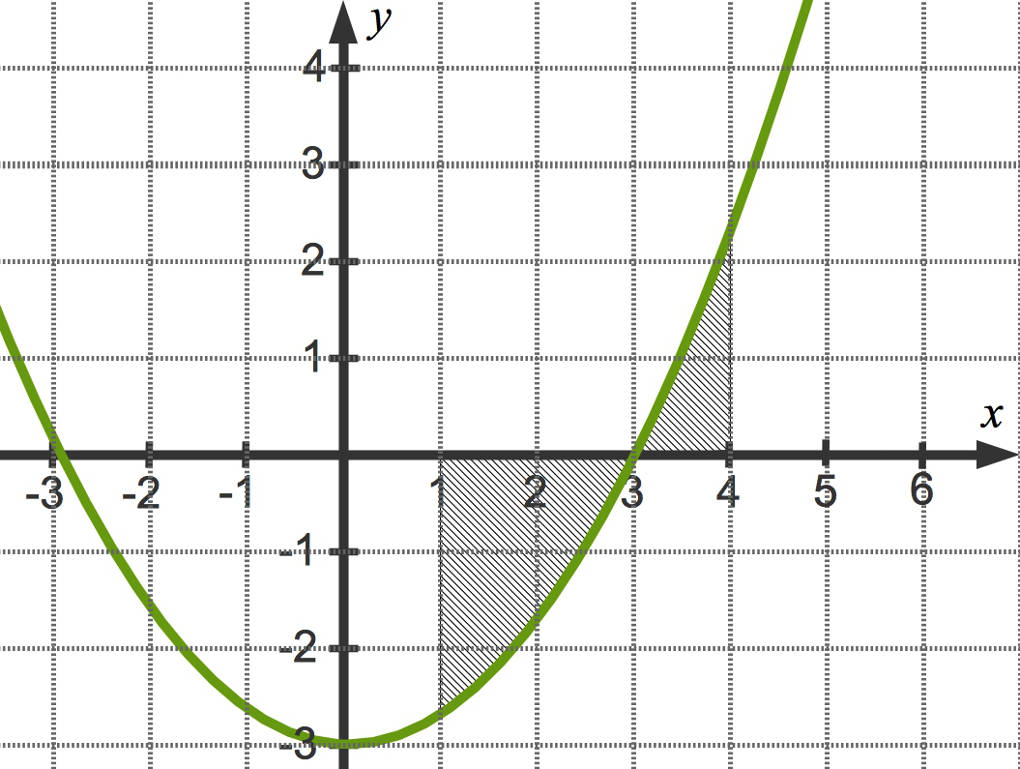
In diesem Beispiel ist $f$ gegeben durch $f(x)=\frac13x^{2}-3$ und das betrachtete Intervall ist $I=[1;4]$.
Du darfst in diesem Fall nicht von der unteren (hier $1$) bis zur oberen (hier $4$) Integrationsgrenze „durchintegrieren“. In diesem Fall würdest du die sogenannte Flächenbilanz erhalten.
Du musst zunächst die Nullstelle berechnen. Diese ist gegeben durch $x=3$. Nun musst du intervallweise die Flächenstücke berechnen. Dabei greifst du auf die beiden oben genannten Fälle zurück:
- Über dem Intervall $[1;3]$ liegt die Fläche komplett unterhalb der $x$-Achse. Damit erhältst du den Inhalt des linken Flächenstücks wie folgt:
$\begin{array}{rcl}A_1&=&\left|\int\limits_1^3~\left(\frac13x^2-3\right)~dx\right|=\left|\left[\frac19x^3-3x\right]_1^3\right|\\ &=&\left|\left(\frac193^3-3\cdot 3\right)-\left(\frac191^3-3\cdot 1\right)\right|=\left|-\frac{28}9\right|=\frac{28}9\end{array}$
- Über dem Intervall $[3;4]$ liegt die Fläche komplett oberhalb der $x$-Achse. Du rechnest dann so:
$A_2=\int\limits_3^4~\left(\frac13x^2-3\right)~dx=\left[\frac19x^3-3x\right]_3^4=\left(\frac194^3-3\cdot 4\right)-\left(\frac193^3-3\cdot 3\right)=\frac{10}9$.
- Schließlich addierst du die beiden Teilflächen und erhältst folgende Gesamtfläche:
$A=A_{1}+A_{2}=\frac{28}{9}+\frac{10}{9}=\frac{38}{9}$.
Flächen zwischen Funktionsgraphen
Schließlich kann ein Flächenstück auch von zwei Funktionsgraphen eingeschlossen werden.
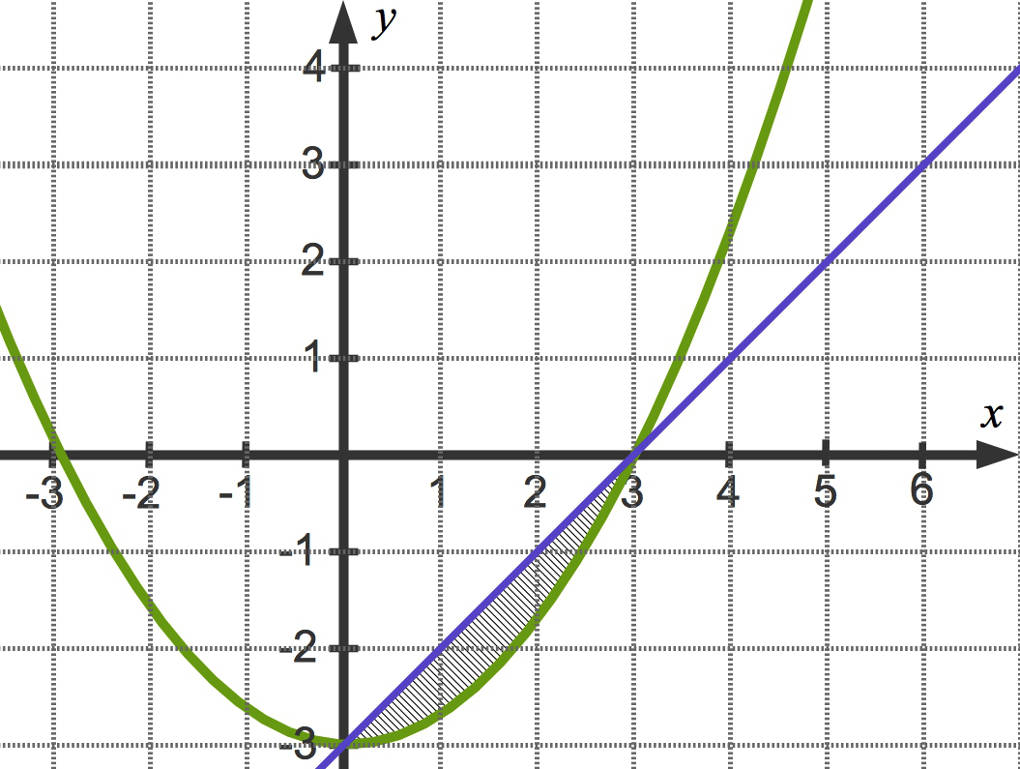
Hier siehst du die Parabel zu der Funktion $f$ mit $f(x)=\frac13x^{2}-3$ sowie die Gerade zu der Funktion $g$ mit $g(x)=x-3$.
Zur Berechnung der schraffierten Fläche gehst du nun wie folgt vor:
- Berechne die beiden Schnittstellen. Löse hierfür die Gleichung $f(x)=g(x)$. So erhältst du $x=0$ sowie $x=3$. Diese beiden Schnittstellen sind die Integrationsgrenzen.
- Ermittle die Differenzfunktion $d(x)=g(x)-f(x)=x-3-\left(\frac13x^{2}-3\right)=x-\frac13x^{2}$. Die Reihenfolge der Differenz ergibt sich daraus, dass die Gerade auf dem Intervall $[0;3]$ oberhalb der Parabel liegt.
- Nun kannst du den Inhalt der Fläche so berechnen:
$A=\int\limits_0^3~\left(x-\frac13x^2\right)~dx=\left[\frac12x^2-\frac19x^3\right]_0^3=\left(\frac123^2-\frac193^3\right)-\left(\frac120^2-\frac190^3\right)=\frac{3}2$
Anmerkung:
- Auch hier können die Integrationsgrenzen bereits in der Aufgabenstellung vorgegeben sein.
- Wenn du nicht weißt, welcher der beiden Funktionsgraphen oberhalb liegt, kannst du die Fläche ebenfalls berechnen. Du verwendest dann den Betrag des bestimmten Integrals.
- Sollten die beiden Funktionen mehr als zwei Schnittstellen haben, musst du wieder intervallweise die Flächenstücke berechnen und schließlich die Teilflächen addieren.
Variationen der Aufgabenstellung
Die Flächenberechnung kommt oftmals in anderer Form vor:
- Du musst eine Gerade so verschieben, dass ein Flächenstück in einem gewissen Verhältnis geteilt wird.
- Du sollst eine Funktion rekonstruieren. Dabei soll die Funktion eine gegebene Integraleigenschaft besitzen.
Alle Videos zum Thema
Videos zum Thema
Bestimmte Integrale und Flächen mit Integralen berechnen (3 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Bestimmte Integrale und Flächen mit Integralen berechnen (3 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Primzahlen
- Geometrische Lagebeziehungen
- Rechteck
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Quadrat
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Was Ist Eine Viertelstunde
- Prisma
- Mitternachtsformel
- Grundrechenarten Begriffe
- Dreiecksarten
- Quader
- Satz Des Pythagoras
- Dreieck Grundschule
- Erste Binomische Formel
- Kreis
- Standardabweichung
- Flächeninhalt
- Volumen Kugel
- Zahlen In Worten Schreiben
- Meter
- Orthogonalität
- Schriftlich Multiplizieren
- Brüche Multiplizieren
- Potenzgesetze
- Distributivgesetz
- Flächeninhalt Dreieck
- Rationale Zahlen
- Volumen Berechnen
- Brüche Addieren
- Kongruenz
- Exponentialfunktion
- Scheitelpunktform
- Logarithmus
- Erwartungswert
- Skalarprodukt
- Primfaktorzerlegung
- Quadratische Ergänzung
- Zinseszins
- Geradengleichung Aus Zwei Punkten Bestimmen
- Sinusfunktion






 Bestimmte Integrale und Flächeninhalte
Bestimmte Integrale und Flächeninhalte
 Integralrechnung – Fläche zwischen zwei Graphen
Integralrechnung – Fläche zwischen zwei Graphen
 Fläche zwischen Funktionsgraphen mit Integralen berechnen
Fläche zwischen Funktionsgraphen mit Integralen berechnen









