Alternativtests
Mit Hilfe von statistischen Tests kann man ausgehend von einer Stichprobe die Gültigkeit einer Annahmen untersuchen.
Inhaltsverzeichnis zum Thema
Das Abiturproblem
Euer Mathelehrer behauptet, dass letztes Jahr $92\%$ der Berliner Schüler das Abitur gemeistert haben. Das wäre ja fast zu schön, um wahr zu sein! Im Internet lest ihr aber, dass es angeblich nur $74\%$ gewesen sind. Hat er also unrecht? Oder stimmt die Aussage aus dem Internet nicht?
Ihr wisst tatsächlich die Ergebnisse von ein paar Schülern. Das ist eure Stichprobe mit der Anzahl $n=38$. Sie stammt aus der Grundgesamtheit aller Berliner Schüler, die letztes Jahr zum Abitur angetreten sind. Wie könnt ihr damit zeigen, welche Aussage eher stimmt? Du schlägst vor, euren Mathelehrer mit seinen eigenen Waffen zu schlagen: mit einem Hypothesentest.
Hypothesentest
Um Hypothesen zu testen, bietet sich in der Statistik ein Hypothesentest an. Dieser dient als Entscheidungsgrundlage. Er ist meist wie folgt aufgebaut:
Es wird eine Nullhypothese $H_0$ und eine Alternativhypothese $H_1$ aufgestellt. Die Hypothesen werden so gewählt, dass sie sich gegenseitig ausschließen.
Eine binomialverteilte Zufallsvariable $X$ wird als Prüfgröße herangezogen, welche in der Stichprobe $n$ verschiedene, ganzzahlige Werte $x$ annehmen kann.
Das Signifikanzniveau wird festgelegt. Es wird zwischen zwei Irrtumswahrscheinlichkeiten unterschieden: Fehler 1. Art $p=\alpha$ : $H_0$ wird abgelehnt, obwohl sie wahr ist. Fehler 2. Art $p=\beta$ : $H_0$ wird angenommen, obwohl sie falsch ist. Normalerweise wird für $\alpha=0,05$ gewählt. Damit werden die zwei Fehler etwa gleich groß.
Damit werden Annahme- und Verwerfungsbereiche für die Hypothesen festgelegt.
Je nach Anforderung und Aufgabenstellung können die Schritte $3$ und $4$ auch vertauscht sein. Werden zwei konkrete Vermutungen gegeneinander getestet, ist es ein Alternativtest.
Alternativtest
Es wird also zunächst davon ausgegangen, dass die Aussage eures Mathelehrers stimmt. Daher ist sie die Nullhypothese. Die Wahrscheinlichkeit im Internet ist die Alternative.
$H_0: p_0=0,92$ und $H_1: p_1=0,74$
Die Zufallsvariable $X$ sollte also binomialverteilt sein mit den Parametern $n=38$ und $p=0,92$. Es gilt also:
$X\sim B(38;0,92;k)$
Sie kann die Werte $x=0,1,…,38$ (je nach Stichprobe) annehmen und hat folgenden Erwartungswert $\mu_0$:
$ \mu_0=n\cdot p=38\cdot 0,92 = 34,96\approx 35 $
Jetzt überlegst du dir Folgendes: Wenn $X$ tatsächlich so verteilt ist, werden etwa $35$ von $38$ erwartet, die das Abitur geschafft haben. Sind es aber viel weniger, würde das eher für die Alternativhypothese sprechen. Der Test ist linksseitig, da kleine Werte gegen die Nullhypothese sprechen.
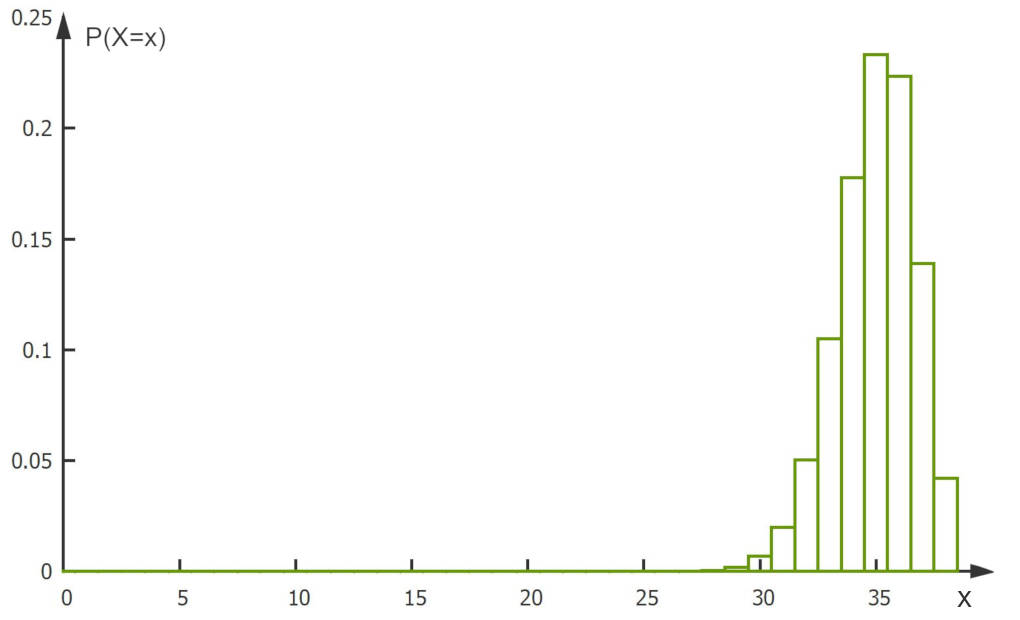
Als $\alpha$-Fehler wird $5\%$ gewählt. Das heißt, bis zu einem kritischen Wert $k$ wird die Aussage eures Mathelehrers abgelehnt. Der Verwerfungsbereich von $H_0$ ist also
$\bar{A}={0;…;k}$.
Dieser Wert $k$ wird mit einer Tabelle der kumulierten Wahrscheinlichkeiten von $B(38;0,92;k)$ bestimmt:
$ P(X\leq k)\leq \alpha $
Es ist $P(X\leq 31)\approx 0,029$ und $P(X\leq 32)\approx 0,079$. Daher wählst du als Ablehnungsbereich für $H_0$ gleich
$\bar{A}={0;…;31}$.
Die Wahrscheinlichkeit $H_0$ abzulehnen, obwohl sie zutrifft, ist damit sogar kleiner, nämlich etwa $3\%$.
Damit lässt sich auch der Fehler 2. Art im Hypothesentest bestimmen. Angenommen, dass die Alternativhypothese stimmt, dann ist $X$ anders verteilt mit $p_1=0,74$. Allerdings war trotzdem $k$ größer als $31$ und es wurde $H_0$ angenommen. Das tritt mit folgender Wahrscheinlichkeit auf:
$ \beta=P(X >31)=B(38;0,74;32)+ B(38;0,74;33)+…+ B(38;0,74;38)\\ \beta= 1-P(X\leq 32) = 1-0,954=0,046 $
Der $\beta$-Fehler ist also etwa $4,6\%$. Von den $38$ Schülern, die ihr kennt, haben es tatsächlich nur $30$ geschafft. Triumphierend legt ihr eure Ergebnisse eurem Mathelehrer vor. Der versucht sich natürlich rauszureden. Chancenlos. Ihr habt ihn gnadenlos überführt!
Alle Videos zum Thema
Videos zum Thema
Alternativtests (2 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Alternativtests (2 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Primzahlen
- Geometrische Lagebeziehungen
- Rechteck
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Quadrat
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Was Ist Eine Viertelstunde
- Prisma
- Mitternachtsformel
- Grundrechenarten Begriffe
- Dreiecksarten
- Quader
- Satz Des Pythagoras
- Dreieck Grundschule
- Erste Binomische Formel
- Kreis
- Standardabweichung
- Flächeninhalt
- Volumen Kugel
- Zahlen In Worten Schreiben
- Meter
- Orthogonalität
- Schriftlich Multiplizieren
- Brüche Multiplizieren
- Potenzgesetze
- Distributivgesetz
- Flächeninhalt Dreieck
- Rationale Zahlen
- Volumen Berechnen
- Brüche Addieren
- Kongruenz
- Exponentialfunktion
- Scheitelpunktform
- Logarithmus
- Erwartungswert
- Skalarprodukt
- Primfaktorzerlegung
- Quadratische Ergänzung
- Zinseszins
- Geradengleichung Aus Zwei Punkten Bestimmen
- Sinusfunktion



 Testen von Hypothesen – Alternativtest
Testen von Hypothesen – Alternativtest
 Hypothesentest – Signifikanz und Irrtumswahrscheinlichkeit
Hypothesentest – Signifikanz und Irrtumswahrscheinlichkeit









