Gegenseitige Lage Punkt-Ebene
In der analytischen Geometrie behandelst du unter anderem Ebenen und Punkte. Dabei untersuchst du die relative Lage von Punkten zu Ebenen.
Beliebteste Videos
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Punkte und Ebenen im Raum
- Die gegenseitige Lage Punkt-Ebene
- Lagebeziehung Punkt-Ebene
- Abstandsberechnung
- Vierecke
Punkte und Ebenen im Raum
Punkte
Ein Punkt im Raum $\mathbb{R}^{3}$ ist zum Beispiel $A(2|-1|5)$. Dieser Punkt hat drei Koordinaten, die $x$- oder auch $x_{1}$-, die $y$- oder auch $x_{2}$- sowie die $z$- oder auch $x_{3}$-Koordinate.
Ebenen
Ebenen sind entweder durch einen Punkt und zwei Vektoren oder durch drei Punkte gegeben. Dabei muss gelten:
- Die Vektoren sind nicht kollinear.
- Die drei Punkte liegen nicht auf einer Geraden.
Eine Parametergleichung sieht so aus:
$E:\vec x=\vec a+r\cdot \vec u+s\cdot \vec v$
Dabei ist
- $\vec x$ ein Vektor, der auf einen beliebigen Punkt der Ebene zeigt,
- $\vec a$ ein Vektor, der auf einen gegebenen Punkt der Ebene zeigt, der Stützvektor,
- $\vec u$ sowie $\vec v$ die Richtungsvektoren und
- $r\in\mathbb{R}$ sowie $s\in\mathbb{R}$ Parameter.
Ebenen können auch in anderen Formen dargestellt werden:
Die Normalenform
$E:\left(\vec x-\vec a\right)\star \vec n=0$
Dabei ist $\vec n$ ein Normalenvektor der Ebene. Dieser steht senkrecht zu der Ebene.
Die Hessesche Normalenform
Zur Abstandsberechnung benötigst du die Hessesche Normalenform (HNF):
$E:\left(\vec x-\vec a\right)\star \vec n^{*}=0$
Dabei ist $\vec n^{*}=\frac{1}{\left|\vec n\right|}\vec n$ der auf die Länge $1$ normierte Normalenvektor.
Die Koordinatenform
Die Koordinatenform erhältst du ausgehend von der Normalenform:
$n_{x}\cdot x+n_{y}\cdot y+n_{z}\cdot z=\vec n\star \vec a$
Dabei sind $n_{x}$, $n_{y}$ und $n_{z}$ die Koordinaten des Normalenvektors der Ebene.
So, nun kann es losgehen.
Die gegenseitige Lage Punkt-Ebene
Wir untersuchen zunächst einmal die gegenseitige Lage von Punkt und Ebene. Hierfür kannst du jede der vorgestellten Darstellungsformen verwenden:
- Die Parametergleichung: Du führst eine Punktprobe durch. Setze den Ortsvektor des Punktes für $\vec x$ in die Ebenengleichung ein. So erhältst du ein lineares Gleichungssystem mit drei Gleichungen und den beiden Parametern als Unbekannten. Dieses Vorgehen ist recht aufwändig. Darum ist es ratsam, eher die Normalenform oder Koordinatenform zu verwenden.
- Die Normalenform: Auch hier setzt du den Ortsvektor des Punktes für $\vec x$ in die Ebenengleichung ein. Nun musst du noch prüfen, ob tatsächlich $0$ herauskommt, dann liegt der Punkt in der Ebene. Andernfalls liegt der Punkt nicht in der Ebene.
- Die Koordinatenform: Setze die Koordinaten des Punktes für $x$, $y$ und $z$ in die Koordinatenform ein. Auch hier prüfst du, ob die Gleichung erfüllt ist oder nicht. Ist sie erfüllt, liegt der Punkt in der Ebene, andernfalls nicht.
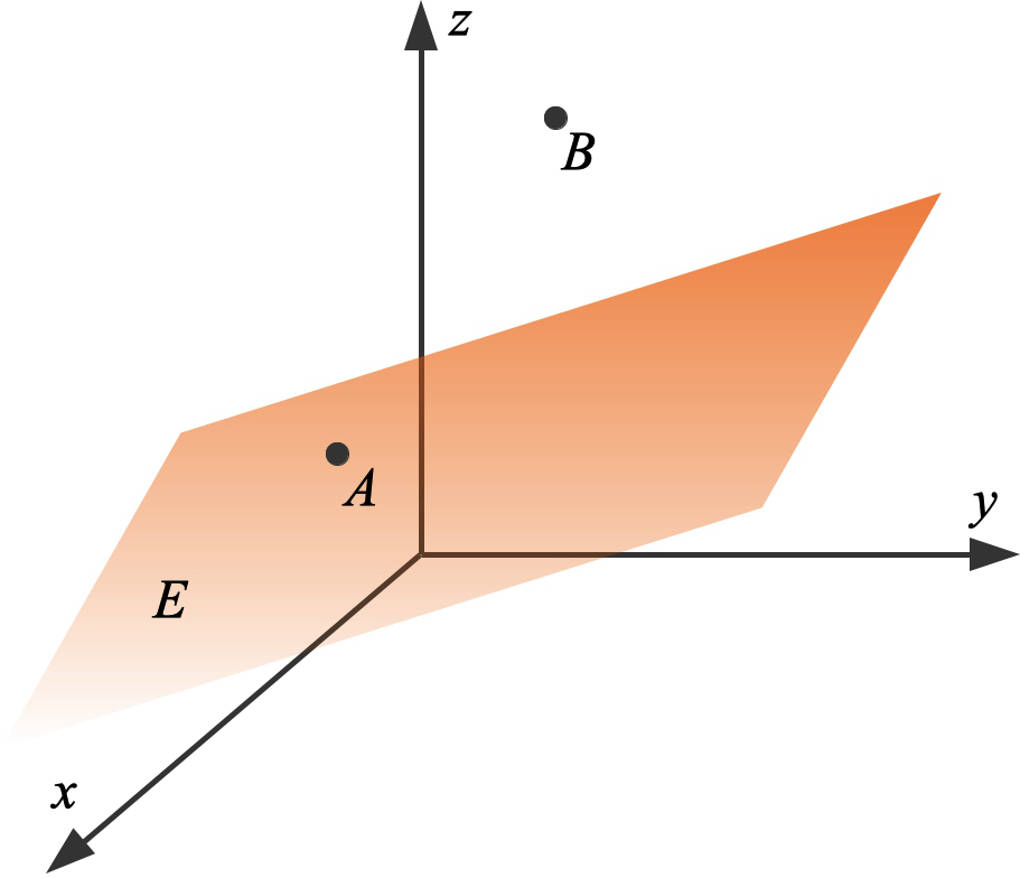
Du siehst, bei den letzten beiden Verfahren setzt du ein und musst keine Gleichung lösen. Dafür musst du gegebenenfalls eine Parameterform erst einmal in eine Normalen- oder Koordinatenform umformen. Es lohnt sich!
Lagebeziehung Punkt-Ebene
Beispiel: Punkt liegt in der Ebene
Wir schauen uns nun ein Beispiel an. Gegeben sei die Ebene $E$ in Koordinatenform mit $E:2x+y-2z=6$ sowie der Punkt $A(3|2|1)$.
Setze die Koordinaten von $A$ in die Koordinatenform ein: $2\cdot 3+2-2\cdot 1=6+2-2=6$ ✓
Perfekt, dieser Punkt liegt in der Ebene.
Beispiel: Punkt liegt nicht in der Ebene
Dieses Mal schauen wir uns eine Ebene in Normalenform an:
$E:\left(\vec x-\begin{pmatrix} 3\\2\\1 \end{pmatrix}\right)\star\begin{pmatrix} 2\\1\\-2 \end{pmatrix}=0$
Du sollst prüfen, ob der Punkt $B(7|3|1)$ in dieser Ebene liegt:
$\left(\begin{pmatrix} 7\\3\\1 \end{pmatrix}-\begin{pmatrix} 3\\2\\1 \end{pmatrix}\right)\star\begin{pmatrix} 2\\1\\-2 \end{pmatrix}=0$
Rechne die Vektordifferenz in der Klammer aus:
$\begin{pmatrix} 4\\1\\0 \end{pmatrix}\star\begin{pmatrix} 2\\1\\-2 \end{pmatrix}=0$
Nun kannst du das Skalarprodukt berechnen und erhältst $9=0$. Diese Aussage ist nicht richtig. Der Punkt $B$ liegt somit nicht in der Ebene.
Wenn ein Punkt nicht in einer Ebene liegt, kannst du den Abstand des Punktes zu dieser Ebene berechnen.
Abstandsberechnung
Hierfür kannst du verschieden vorgehen:
- Du erstellst eine Lotgerade. Diese hat als Stützvektor den Ortsvektor des Punktes und als Richtungsvektor den Normalenvektor der Ebene. Diese Gerade schneidet die Ebene in dem Lotfußpunkt. Der Abstand dieses Lotfußpunktes zu dem Punkt ist der gesuchte Abstand.
- Du kannst auch die Hessesche Normalenform verwenden. In diese setzt du für $\vec x$ den Ortsvektor des Punktes ein. Der Betrag des erhaltenen Ergebnisses ist der gesuchte Abstand.
$d(P;E)=\left|\left(\vec p-\vec a\right)\star\vec n^{*}\right|$
- Schließlich kannst du auch die folgende Abstandsformel verwenden:
$d(P;E)=\left|\dfrac{n_x\cdot p_x+n_y\cdot p_y+n_z\cdot p_z-\vec n\star \vec a}{\sqrt{n_x^2+n_y^2+n_z^2}}\right|$
Dabei sind $p_{x}$, $p_{y}$ und $p_{z}$ die Koordinaten des Punktes $P$, $n_{x}$, $n_{y}$ und $n_{z}$ die Koordinaten des Normalenvektors $\vec n$ und $\vec a$ der Stützvektor der Ebene.
Mit Hilfe dieser Formel berechnen wir nun den Abstand des oben angegebenen Punktes $B$ von der Ebene $E$ in Koordinatenform:
$d(P;E)=\left|\dfrac{2\cdot 7+ 3-2\cdot 1-6}{\sqrt{2^2+1^2+(-2)^2}}\right|=\frac93=3$
Vierecke
Du kannst schließlich auch prüfen, ob ein Viereck bei gegebenen vier Punkten in einer Ebene liegt. Hierfür bestimmst du mit drei der vier Punkte eine Ebene in der Drei-Punkt-Form: Der Ortsvektor von einem der drei Punkte ist der Stützvektor und die von diesem Punkt ausgehenden Verbindungsvektoren zu den beiden übrigen Punkten sind die Richtungsvektoren. Übrigens: Die Richtungsvektoren dürfen nicht kollinear sein. Ansonsten liegt keine Ebene vor.
Schließlich prüfst du, ob der verbleibende Punkt auch in der Ebene liegt. Ist dies der Fall, so liegt das Viereck in der Ebene. Andernfalls ist das Viereck gebogen. Das kannst du dir so vorstellen wie ein Blatt Papier, welches du biegst.
Alle Videos zum Thema
Videos zum Thema
Gegenseitige Lage Punkt-Ebene (4 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Gegenseitige Lage Punkt-Ebene (4 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Primzahlen
- Geometrische Lagebeziehungen
- Rechteck
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Quadrat
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Was Ist Eine Viertelstunde
- Prisma
- Mitternachtsformel
- Grundrechenarten Begriffe
- Dreiecksarten
- Quader
- Satz Des Pythagoras
- Dreieck Grundschule
- Erste Binomische Formel
- Kreis
- Standardabweichung
- Flächeninhalt
- Volumen Kugel
- Zahlen In Worten Schreiben
- Meter
- Orthogonalität
- Schriftlich Multiplizieren
- Brüche Multiplizieren
- Potenzgesetze
- Distributivgesetz
- Flächeninhalt Dreieck
- Rationale Zahlen
- Volumen Berechnen
- Brüche Addieren
- Kongruenz
- Exponentialfunktion
- Scheitelpunktform
- Logarithmus
- Erwartungswert
- Skalarprodukt
- Primfaktorzerlegung
- Quadratische Ergänzung
- Zinseszins
- Geradengleichung Aus Zwei Punkten Bestimmen
- Sinusfunktion







 Gegenseitige Lage Punkt-Ebene
Gegenseitige Lage Punkt-Ebene
 Abstände im Raum – Zusammenfassung
Abstände im Raum – Zusammenfassung
 Abstand Punkt-Ebene – Anwendung
Abstand Punkt-Ebene – Anwendung
 Abstandsberechnung mit der Hesseschen Normalenform – Übung
Abstandsberechnung mit der Hesseschen Normalenform – Übung









