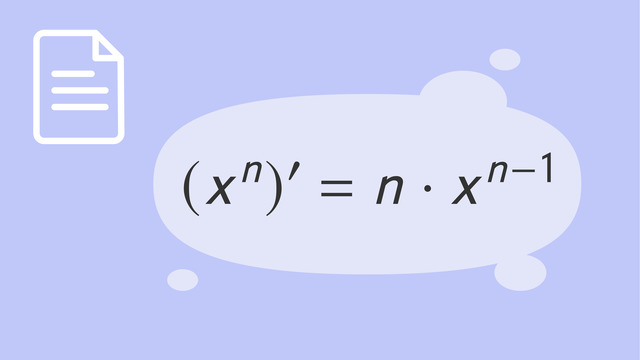Summenregel

in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
Grundlagen zum Thema Summenregel
Nach dem Schauen dieses Videos wirst du in der Lage sein, Funktionen, die sich aus Summen oder Differenzen zusammensetzen, abzuleiten
Zunächst lernst du, dass du laut der Summenregel die Summe von zwei Funktionen ableiten kannst, indem du die Funktionen jeweils einzeln ableitest. Anschließend erfährst du, wie du eine konstante Zahl ableitest. Abschließend erfährst du, wie du eine Funktion mehrfach ableiten kannst.

Das Video beinhaltet Schlüsselbegriffe, Bezeichnungen und Fachbegriffe wie Summenregel, Konstantenregel, Ableitungsfunktion, erste Ableitung, zweite Ableitung und höhere Ableitung.
Bevor du dieses Video schaust, solltest du bereits die Potenz- und Faktorregel kennen. Außerdem solltest du grundlegendes Wissen zu Ableitungen haben.
Nach diesem Video wirst du darauf vorbereitet sein, zu lernen, wie man die Produktregel für Ableitungen anwendet.
Transkript Summenregel
Wenn man gerade so vor sich her rechnet, denkt man sich meistens gar nichts Böses. Man macht einfach das, was einem richtig erscheint, schon hat man sich auf Glatteis begeben und wieder einen Fehler gemacht! Umso schöner ist es doch, wenn eine Rechenregel mal einfach ist und wirklich so funktioniert, wie man sich das vorstellt! Und so ist die Summenregel bei Ableitungen. Versprochen! Wie wir eine Funktion wie diese hier ableiten können, wissen wir schon. Einfach den Exponenten als Faktor nach vorne ziehen, und um eins verringern. Der Faktor, der schon vorher da stand, bleibt beim Ableiten erhalten und wird jetzt noch mit dem neuen Faktor multipliziert. Check! Aber wie leiten wir denn eine Funktion ab, bei der zusätzlich noch so eine Potenz von x addiert wird? Ganz einfach! Wir leiten auch diese Potenz ab und addieren die erhaltenen Ableitungen. Ganz einfach und intuitiv! Natürlich können wir das auch wieder formal als allgemeine Regel formulieren. Wenn wir eine Funktion haben, die sich aus der Summe von zwei oder mehreren Termen zusammensetzt, die ein x enthalten – wir betrachten diese als Teilfunktionen „u von x“ und „v von x“ – können wir diese Funktion ableiten, indem wir jede Teilfunktion einzeln ableiten und die Ableitungen addieren. Schauen wir uns dazu noch ein paar Beispiele an! Wie sieht es denn mit dieser Funktion aus? Hier steht ein Minus anstatt von einem Plus zwischen den Potenzen. Können wir trotzdem die Summenregel anwenden? Ja, denn eine Differenz können wir ja genauso gut als Summe schreiben, wenn wir das Minus einklammern. Wir leiten also beide Potenzen einzeln ab, können noch vereinfachen, und fertig ist die Ableitungsfunktion. Genauso funktioniert es auch, wenn wir mehr als nur zwei Summanden haben. Wir können uns jeden einzeln vorknöpfen, und die Potenzen so Schritt für Schritt ableiten. Und was passiert mit der Zahl am Ende? Dabei handelt es sich um eine „additive Konstante“. Anders als bei multiplikativen Konstanten – also Zahlen, die mit einem x-Term multipliziert werden und somit bei der Ableitung erhalten bleiben – werden additive Konstanten beim Ableiten zu Null. Das können wir uns mit der Potenzregel deutlich machen. Denn fünf können wir auch schreiben als „fünf mal eins“, also „fünf mal x hoch null“. Wenn wir jetzt nach der Potenzregel ableiten, ziehen wir die null als Faktor nach vorne. Und irgendetwas mal Null ist immer null. Da wir die Null nicht extra aufschreiben müssen, fällt eine additive Konstante beim Ableiten also einfach weg. Das wird manchmal auch „Konstantenregel“ genannt. Wir können uns merken: additive Konstanten – sprich einfache Zahlen ohne X – fallen beim Ableiten einfach weg. Und das war es eigentlich auch schon, was du zur Summenregel wissen musst. Jetzt können wir Funktionen wie diese hier problemlos ableiten. Das wiederum wirft aber eine klitzekleine neue Frage auf: Können wir die Ableitungsfunktion eigentlich auch ableiten? Wir können uns ja mal ganz vorsichtig ran wagen und die Funktion behutsam Schritt für Schritt ableiten. Scheint geklappt zu haben! Tatsächlich haben wir gerade eine höhere – um genau zu sein die zweite – Ableitung gebildet. „f-zwei-Strich von x“. Genauso können wir jetzt auch „f drei Strich“ – also die dritte Ableitung bilden und so weiter. Leiten wir eine Funktion f „n-mal“ ab, erhalten wir die n-te Ableitung. Bei ganzrationalen Funktionen, wie dieser hier, ist die nächste Ableitung ab einem gewissen Punkt dann einfach immer gleich null. Je höher die Ableitung, desto einfacher wird es! Wir fassen das Wichtigste auf einen Blick zusammen. Die Summenregel sagt uns, dass wir eine Funktion, die aus einer Summe mehrerer Terme besteht, die ein x enthalten, ableiten können, indem wir diese Terme als Teilfunktionen betrachten und einfach einzeln ableiten. Auch wenn diese Regel Summenregel genannt wird, gilt sie genauso für Differenzen. Additive Konstanten, also einfache Zahlen ohne x, die addiert oder subtrahiert werden, fallen beim Ableiten weg. Zusammen mit der Potenz- und Faktorregel können wir Funktionen so beliebig oft ableiten. Also nicht nur die erste Ableitung, sondern auch die zweite, dritte, oder ganz allgemein ausgedrückt: eine höhere Ableitung bilden. Und sollten dabei mit ein bisschen Übung auch nicht mehr allzu schnell auf dem Hosenboden landen.
Summenregel Übung
-
Gib die Summenregel an.
TippsWerden mehrere Terme addiert, so können wir sie einzeln ableiten.
Beispiel:
$f(x)=x^4+2x$
$f'(x)=4x^3+2$LösungEine Potenzfunktion können wir mithilfe der Potenzregel ableiten:
$f(x)=x^n \quad \rightarrow \quad f'(x)=nx^{n-1}$Um eine Funktion abzuleiten, welche aus der Summe mehrerer Teilfunktionen besteht, leiten wir zuerst jeden Summanden einzeln ab. Anschließend addieren wir die einzelnen Ableitungen.
Wir schreiben:$\begin{array}{rcccc} f(x) &=& u(x) &+& v(x) \\ f'(x) &=& u'(x) &+& v'(x) \end{array}$
Beispiel:
$f(x)=4x^3+3x^2$
$f'(x)=3\cdot 4x^2 + 2 \cdot 3x = 12x^2+6x$Die Summenregel gilt auch für Differenzen:
Beispiel:
$f(x)=-3x^2-5x$
$f'(x)=-3 \cdot 2x - 5 = -6x-5$ -
Beschreibe Eigenschaften der Summenregel.
TippsUnter einer additiven Konstante verstehen wir eine Zahl, welche addiert wird.
Beispiel:
$f(x)= 5x^3-3x^2$
$f'(x) = 15x^2-6x$
$f''(x) = 30x-6$
$f'''(x) = 30$LösungSummenregel:
Um eine Funktion abzuleiten, welche aus der Summe mehrerer Funktionen besteht, leiten wir zuerst jeden Summanden einzeln ab. Anschließend addieren wir die einzelnen Ableitungen. Wir schreiben:
$\begin{array}{rcccc} f(x) &=& u(x) &+& v(x) \\ f'(x) &=& u'(x) &+& v'(x) \end{array}$Wir betrachten nun einige Spezialfälle der Summenregel:
1. Differenzen:
Da wir eine Differenz auch als Summe schreiben können, gilt hier auch die Summenregel.
Beispiel: $f(x) = 2x^3-x^2 = 2x^3 + (-x^2) \quad \to \quad f'(x) = 6x^2 + (-2x) = 6x^2-2x$
korrekte Aussage: Die Summenregel gilt auch für Funktionen, welche aus der Differenz mehrerer Terme besteht.2. Additive Konstanten:
Unter einer additiven Konstante verstehen wir eine Zahl, welche addiert wird. Diese fällt nach der Potenzregel beim Ableiten weg:
Beispiel: $f(x)= 4x^2 + 3 = 4x^2 + 3x^0 \quad \to \quad f'(x) = 8x + 0 \cdot 3x^{-1} = 8x+0 = 8x$
falsche Aussage: Eine additive Konstante bleibt beim Ableiten erhalten.3. Höhere Ableitungen:
Wir können die Summenregel auch auf höhere Ableitungen anwenden:
Beispiel: $f(x)= 5x^3-3x^2 ~\to~ f'(x) = 15x^2-6x ~\to~ f''(x) = 30x-6 ~\to~ f'''(x) = 30$
falsche Aussage: Die Summenregel gilt nur für die erste Ableitung.4. Produkte:
Die Summenregel gilt nur für Summen und Differenzen mehrerer Funktionen, nicht aber für Produkte.
richtige Aussage: Besteht eine Funktion aus dem Produkt mehrerer Terme, so können wir die Summenregel nicht anwenden. -
Berechne die Ableitungen der Funktionen.
TippsBeispiel:
$f(x)=3x^6-7x^2+x$
$f'(x) = 18x^5-14x+1$Eine additive Konstante fällt beim Ableiten weg.
LösungUm eine Funktion abzuleiten, welche aus der Summe mehrerer Potenzen besteht, leiten wir zuerst jeden Summanden einzeln ab. Anschließend addieren wir die einzelnen Ableitungen.
Summenregel:
$\begin{array}{rcccc} f(x) &=& u(x) &+& v(x) \\ f'(x) &=& u'(x) &+& v'(x) \end{array}$Dies gilt auch für Differenzen, da wir diese durch Klammern als Summe schreiben können.
Die einzelnen Summanden können wir mithilfe der Potenzregel ableiten:
$f(x)=x^n \quad \rightarrow \quad f'(x)=nx^{n-1}$
Dabei fallen additive Konstanten weg.So ergeben sich folgende Lösungen:
1. Funktion:
$f(x)=4x^2+5x-1$
$f'(x) = 8x +5$2. Funktion:
$f(x)=-\dfrac{1}{2}x^2-4$
$f'(x) = -x$3. Funktion:
$f(x)=x^{-6} - 3x + \dfrac{8}{3} $
$f'(x) = -6x^{-7}-3$4. Funktion:
$f(x)=5x-1{,}2 $
$f'(x) = 5$ -
Ermittle die höheren Ableitungen der Funktionen.
TippsDu kannst die Summenregel auch auf höhere Ableitungen anwenden. Um die zweite Ableitung $f''(x)$ zu bestimmen, leitest du die erste Ableitung $f'(x)$ einfach nach der Summenregel ab.
Achte darauf, dass additive Konstanten beim Ableiten wegfallen, multiplikative Konstanten hingegen erhalten bleiben.
LösungSummenregel:
$\begin{array}{rcccc} f(x) &=& u(x) &+& v(x) \\ f'(x) &=& u'(x) &+& v'(x) \end{array}$Wir können die Summenregel auch auf höhere Ableitungen anwenden:
1. Funktion:
$f(x)=-4x^3-3x^2+4$
$f'(x)=-12x^2-6x$
$f''(x)=-24x-6$
$f''(x) = -24$2. Funktion:
$f(x)=-3x^{-4}-2x+3$
$f'(x)= 12x^{-5}-2$
$f''(x)=-60x^{-6}$
$f'''(x)=360x^{-7}$3. Funktion:
$f(x)=-3x^4-3x^3+x$
$f'(x)= -12x^3-9x^2+1$
$f''(x)=-36x^2-18x$
$f'''(x)=-72x-18$ -
Bestimme die Ableitung der Funktion.
Tipps$f(x)=x^n \quad \rightarrow \quad f'(x)=nx^{n-1}$
Beispiel:
$f(x)=3x^5 \quad \rightarrow \quad f'(x) = 5 \cdot 3x^{5-1} = 15x^4$LösungEine Potenzfunktion können wir mithilfe der Potenzregel ableiten:
$f(x)=x^n \quad \rightarrow \quad f'(x)=nx^{n-1}$Somit ergibt sich für die einzelnen Funktionen:
- $f(x)=2x^3 \quad\quad\rightarrow \quad f'(x) = 3 \cdot 2x^{3-1} = 6x^2$
- $f(x)=5x^2\quad\quad \rightarrow \quad f'(x) = 2 \cdot 5x^{2-1} = 10x$
- $f(x)=-4x^2\quad \ \rightarrow \quad f'(x) = 2 \cdot (-4)x^{2-1} = -8x$
- $f(x)=x^7\ \ \quad\quad \rightarrow \quad f'(x) = 7 \cdot x^{7-1} = 7x^6$
- $f(x)=2x^6\quad\quad \rightarrow \quad f'(x) = 6 \cdot 2x^{6-1} = 12x^5$
-
Entscheide, ab welcher Ableitung alle höheren Ableitungen gleich Null sind.
TippsAb wann die höheren Ableitungen gleich Null sind, hängt vom Grad der Funktion ab.
Die Lösung kann ermittelt werden, indem die höheren Ableitungen der Funktion gebildet werden, bis sich das erste mal eine Ableitung gleich Null ergibt. Alle höheren Ableitungen sind dann auch gleich Null.
LösungWir können die Summenregel auch auf höhere Ableitungen anwenden:
$f(x)=u(x)-v(x)$
$f'(x)=u'(x)+v'(x)$
$f''(x)=u''(x)+v''(x)$
$f'''(x)=u'''(x)+v'''(x)$
und so weiter.Bei ganzrationalen Funktionen sind die höheren Ableitungen ab einem bestimmten Schritt immer gleich Null. Ab wann die Ableitungen gleich Null sind, hängt vom Grad der Funktion ab. Dieser ist gleich dem höchsten Exponenten. Ist der Grad einer Funktion gleich $a$, so sind die höheren Ableitungen ab der $(a+1)$. Ableitung gleich Null.
Begründung: Dies ergibt sich daraus, dass sich der Exponent beim Ableiten jeweils um eins verringert. Sobald der Exponent gleich Null ist, bleibt nur noch eine Konstante übrig, welche bei der folgenden Ableitung gleich Null ist.Bei einer Funktion zweiten Grades beispielsweise sind die Ableitungen also ab $f'''(x)$ gleich Null.
Wir betrachten dementsprechend die gegebenen Funktionen:
1. Funktion:
$f(x)=3x^3-4x+5$
Es handelt sich um eine Funktion dritten Grades. Die Ableitungen sind also ab $f''''(x)$ gleich Null.
Die Ableitungen lauten:- $f'(x)=9x^2-4$
- $f''(x)=18x$
- $f'''(x)=18$
- $f''''(x)=0$
2. Funktion:
$f(x)=4-\dfrac{3x}{2} = 4 - \dfrac{3}{2}x$
Es handelt sich um eine Funktion ersten Grades. Die Ableitungen sind also ab $f''(x)$ gleich Null.
Die Ableitungen lauten:- $f'(x)=-\dfrac{3}{2}$
- $f''(x)=0$
3. Funktion:
$f(x)=\dfrac{x^4-3x^5}{x} - \dfrac{1}{2} = x^3-3x^4 - \dfrac{1}{2} $
Es handelt sich um eine Funktion vierten Grades. Die Ableitungen sind also ab $f'''''(x)$ gleich Null.
Die Ableitungen lauten:- $f'(x)=3x^2-12x^3$
- $f''(x)=6x-36x^2$
- $f'''(x)=6-72x$
- $f''''(x)=-72$
- $f'''''(x)=0$
Hinweis: Die Lösung kann auch ermittelt werden, indem die höheren Ableitungen der Funktion wie angegeben gebildet werden, bis sich das erste mal eine Ableitung gleich Null ergibt. Alle höheren Ableitungen sind dann auch gleich Null.
7.744
sofaheld-Level
6.601
vorgefertigte
Vokabeln
7.912
Lernvideos
37.035
Übungen
34.291
Arbeitsblätter
24h
Hilfe von Lehrer*
innen

Inhalte für alle Fächer und Klassenstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Primzahlen
- Geometrische Lagebeziehungen
- Rechteck
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Quadrat
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Was Ist Eine Viertelstunde
- Prisma
- Mitternachtsformel
- Grundrechenarten Begriffe
- Dreiecksarten
- Quader
- Satz Des Pythagoras
- Dreieck Grundschule
- Erste Binomische Formel
- Kreis
- Standardabweichung
- Flächeninhalt
- Volumen Kugel
- Zahlen In Worten Schreiben
- Meter
- Orthogonalität
- Schriftlich Multiplizieren
- Brüche Multiplizieren
- Potenzgesetze
- Distributivgesetz
- Flächeninhalt Dreieck
- Rationale Zahlen
- Volumen Berechnen
- Brüche Addieren
- Kongruenz
- Exponentialfunktion
- Scheitelpunktform
- Logarithmus
- Erwartungswert
- Skalarprodukt
- Primfaktorzerlegung
- Quadratische Ergänzung
- Zinseszins
- Geradengleichung Aus Zwei Punkten Bestimmen
- Sinusfunktion


 Du möchtest schneller & einfacher lernen?
Du möchtest schneller & einfacher lernen?


 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen