Gegenseitige Lage Gerade-Ebene
Schnittwinkel, Parallelität, Abstand, Gerade in Ebene enthalten, Schnitt, Hessesche Normalform, Abstandsformel, Lotfußpunktverfahren, Normalenvektor
Beliebteste Videos
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
Geraden und Ebenen im Raum
In der analytischen Geometrie werden unter anderem Geraden und Ebenen im dreidimensionalen Raum untersucht. Insbesondere, wie diese zueinander liegen. Anwendung finden diese Berechnungen zum Beispiel in der Luftfahrt. Dort wird die Flugbahn vom Bordcomputer vorherberechnet, um z.B. Kollisionen mit Gebäuden oder auch eine möglichst sanfte Landung zu ermöglichen.

Das Wort analytisch bedeutet eigentlich, dass die Berechnungen meist ohne die Unterstützung eines Computers, also „per Hand“ durchgeführt werden können. Aber keine Panik - den Taschenrechner darfst du natürlich trotzdem benutzen.
Geradengleichung
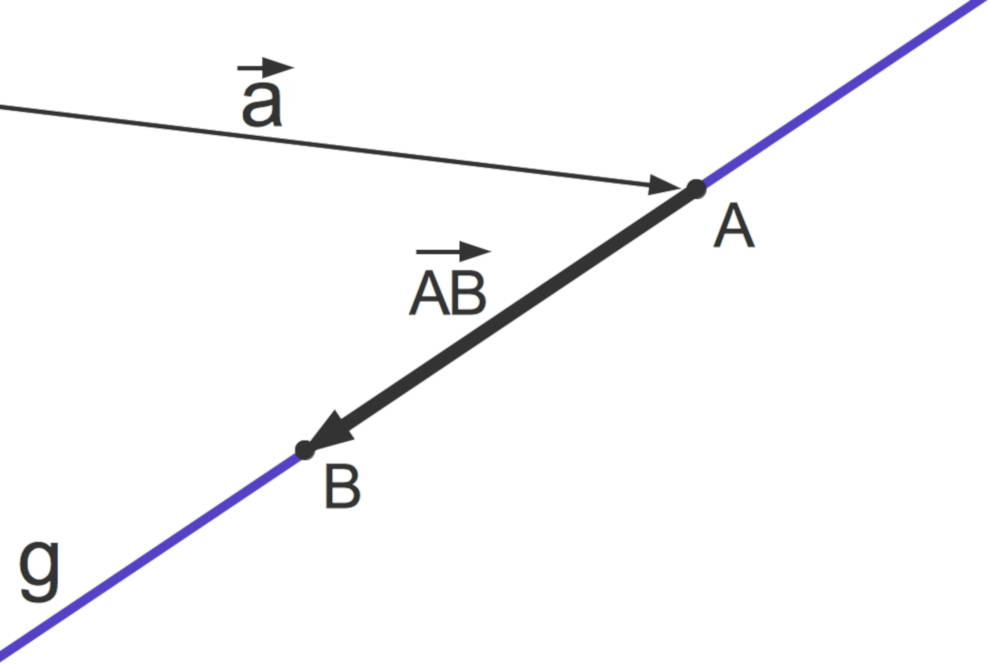
Geraden im Raum können wie im Zweidimensionalen durch zwei Punkte eindeutig bestimmt werden. Mit diesen bzw. deren Vektoren lässt sich die Geradengleichung in Parameterform aufstellen. Den Ortsvektor eines Punkts wählst du dabei als Stützvektor $\vec{a}$. Als Richtungsvektor $\vec{AB}$ verwendest du den Verbindungsvektor der beiden Punkte. Die Geradengleichung hängt vom Parameter $k\in\mathbb{R}$ ab und besitzt dann folgende Form:
$ g: \vec{x}=\vec{a}+k \cdot\vec{AB} $
Das heißt die Koordinaten $x_1$, $x_2$ und $x_3$ der Punkte der Geraden $g$ werden jeweils durch eine Gleichung bestimmt. Diese hängen vom Parameter $k$ ab.
Ebenengleichung
Ebenen im Raum werden z.B. durch drei Punkte eindeutig bestimmt. Mit jeder Dimension des geometrischen Objekts wird also eine Bedingung bzw. ein Punkt mehr benötigt. Ebenengleichungen können in Parameter-, Normalen- oder Koordinatenform angegeben werden.
Die Lagebeziehung einer Geraden zu einer Ebene $E$ kann am einfachsten untersucht werden, wenn die Ebene in Koordinatenform vorliegt. Dafür kann es je nach Aufgabenstellung nötig werden, dass du die Ebenengleichung zunächst in Parameterform aufstellst und anschließend in Koordinatenform bringst:
$ E: a\cdot x_1 + b\cdot x_2 + c\cdot x_3 = d $
Lagebeziehungen Gerade-Ebene
Für die gegenseitige Lage von Gerade und Ebene gibt es grundsätzlich drei Möglichkeiten. Die Gerade kann in der Ebene liegen, parallel zu dieser sein oder sie schneiden. Um welche Lagebeziehung es sich handelt, findest du heraus, indem du die einzelnen Koordinaten der Geraden in die Koordinatenform der Ebene einsetzt. Dadurch erhältst du eine Gleichung, die vom Parameter $k$ der Geraden abhängt.
Gerade liegt in der Ebene
Wenn beim Einsetzen der Parameter $k$ wegfällt und du eine wahre Aussage erhältst, etwa $0=0$, dann ist die Gerade komplett in der Ebene enthalten. Die Punktemenge der Geraden ist damit eine Teilmenge der Punktemenge der Ebene. Oder auch: Alle Punkte auf der Geraden erfüllen die Ebenengleichung.
Gerade ist parallel zur Ebene
Wenn allerdings ein falscher Ausdruck entsteht wie z.B. $13=10$, dann ist das Gegenteil der Fall. Kein einziger Punkt der Geraden erfüllt die Ebenengleichung. Die logische Konsequenz daraus ist, dass die Gerade parallel zur Ebene liegen muss.
Durch die Parallelität hat die Gerade $g$ zur Ebene $E$ überall den gleichen Abstand $d(g,E)$. Du kannst Abstände im Raum durch verschiedene Verfahren und Formeln berechnen. Zum Beispiel durch das Lotfußverfahren oder die hessesche Abstandsformel.
Gerade schneidet Ebene
Nun aber der letzte, spannendste Fall: Die Gerade schneidet die Ebene genau in einem Punkt. Wenn du für $k$ eine konkrete Zahl herausbekommst, dann wird die Ebenengleichung nur für dieses $k$ erfüllt.
Diesen Wert kannst du dann in die Parametergleichung der Geraden einsetzen und erhältst dadurch die Koordinaten des Schnittpunkts $S$.
Unter welchem Winkel $\gamma$ die Gerade die Ebene schneidet, kannst du ebenfalls berechnen. Für diesen Schnittwinkel im Raum benötigst du den Richtungsvektor $\vec{v}$ der Geraden sowie einen Normalenvektor $\vec{n}$ der Ebene. Den kannst du ganz einfach aus der Koordinatenform ablesen. Die Koeffizienten entsprechen dabei den Koordinaten. Diese beiden Vektoren musst du dann nur noch in folgende Gleichung einsetzen:
$ \sin(\gamma) = \dfrac{|\vec{n}\cdot\vec{v}|}{|\vec{n}|\cdot|\vec{v}|} $
Alle Videos zum Thema
Videos zum Thema
Gegenseitige Lage Gerade-Ebene (2 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Gegenseitige Lage Gerade-Ebene (2 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Primzahlen
- Geometrische Lagebeziehungen
- Rechteck
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Quadrat
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Was Ist Eine Viertelstunde
- Prisma
- Mitternachtsformel
- Grundrechenarten Begriffe
- Dreiecksarten
- Quader
- Satz Des Pythagoras
- Dreieck Grundschule
- Erste Binomische Formel
- Kreis
- Standardabweichung
- Flächeninhalt
- Volumen Kugel
- Zahlen In Worten Schreiben
- Meter
- Orthogonalität
- Schriftlich Multiplizieren
- Brüche Multiplizieren
- Potenzgesetze
- Distributivgesetz
- Flächeninhalt Dreieck
- Rationale Zahlen
- Volumen Berechnen
- Brüche Addieren
- Kongruenz
- Exponentialfunktion
- Scheitelpunktform
- Logarithmus
- Erwartungswert
- Skalarprodukt
- Primfaktorzerlegung
- Quadratische Ergänzung
- Zinseszins
- Geradengleichung Aus Zwei Punkten Bestimmen
- Sinusfunktion






 Gegenseitige Lage Gerade-Ebene
Gegenseitige Lage Gerade-Ebene
 Spurgeraden von Ebenen
Spurgeraden von Ebenen









