Aromatizität
Aromate sind stabile ringförmige organische Verbindungen mit delokalisierten Elektronen.
Beliebteste Videos
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
Aromaten
Das klassische Beispiel für einen Aromaten ist das Benzol. Es besteht aus sechs Kohlenstoffatomen und sechs Wasserstoffatomen. Die C-Atome bilden einen Ring. Sie sind über $\sigma$-Bindungen miteinander verknüpft. Außerdem gibt es noch drei $\pi$-Bindungen, die konjugiert sind. Das Molekül als Strukturformel sieht folgendermaßen aus.
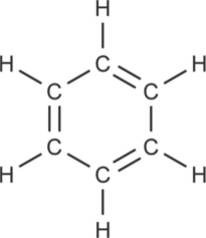
Die Doppelbindungen können aber auch alle um eine Position weiterrutschen. Die tatsächliche Struktur liegt irgendwo in der Mitte. Bei dieser intramolekularen Verschiebung von Elektronen spricht man von Mesomerie. Die $\pi$-Elektronen der Doppelbindungen sind delokalisiert, daher schreibt man sie auch als Kreis in der Mitte des Sechsecks. Die Mesomerie stabilisiert das Molekül und macht es dadurch reaktionsträger. Uns begegnet es vor allem an der Tankstelle, als Antiklopfmittel im Benzin.

Neben den Aromaten gibt es die Aliphaten. Dies sind langkettige Kohlenwasserstoffe, die keine aromatische Mesomerie aufweisen. Aromaten neigen aufgrund der hohen Elektronendichte durch die delokalisierten $\pi$-Elektronen zur elektrophilen Substitution. Dabei greift ein Elektrophil, wie ein $Br^+$, den Aromaten an. Dabei bilden sich ein $\sigma$- und ein $\pi$-Komplex aus. Wasserstoff wird dabei abgespalten.
Kriterien von Aromatizität
Ringe aus Kohlenstoffatomen mit Doppelbindungen sind aber nicht automatisch Aromaten. Dafür bedarf es noch anderer Charakteristika. Für einzelne Ringe kann man die Hückelregel anwenden. Diese besagt, dass ein System aromatisch ist wenn es $4n + 2$ $\pi$-Elektronen enthält. Setzt man für n die 1 ein, erhält man 6 $\Pi$-Elektronen. Dies ist der Fall beim Benzolmolekül. Der nächstgrößere aromatische Ring hätte 10 $\pi$-Elektronen $(4\cdot 2 + 2 =10)$. Ein Aromat muss cyclisch sein. Das heißt, er weist eine geschlossene Ringstruktur auf. Verbindungen mit $4n$ delokalisierten Elektronen werden als antiaromatisch bezeichnet. Größere aromatische Systeme, wie das Pyren (siehe Bild), erfüllen aber die Hückelregel nicht.
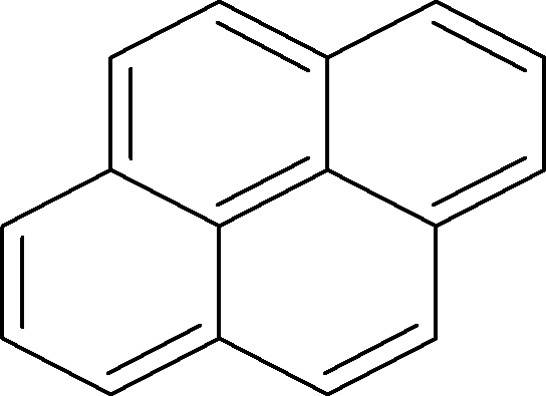
Pyren weist 16 $\pi$-Elektronen auf und wäre somit eigentlich ein Antiaromat. Es ist aber ein Ringsystem, besitzt ausschließlich konjugierte Doppelbindungen und ist planar. Somit ist es zu den Aromaten zu zählen. Es zeigt auch eine hohe Stabilität, was auf die Mesomerie-Stabilisierung von Aromaten hinweist.
Diese Stabilisierung kann auch zur Identifikation von Aromaten benutzt werden. So zeigt sich bei einer Ringöffnung von Aromaten eine positive Energiedifferenz. Das bedeutet, es muss Energie aufgewendet werden, um den Ring zu öffnen. Er ist also sehr stabil. Im Gegensatz dazu zeigen antiaromatische Ringverbindungen eine exotherme Reaktion bei der Ringöffnung. Die Ringöffnung stellt also einen stabilen, energieärmeren Zustand dar als der geschlossene Ring.
Beispiele Aromaten
Aromatische Verbindungen sind sehr vielfältig. Ausgehend vom Benzol können viele Variationen und substituierte Aromaten synthetisiert werden. Reiht man mehrere Sechsringe aneinander, erhält man Aromaten.
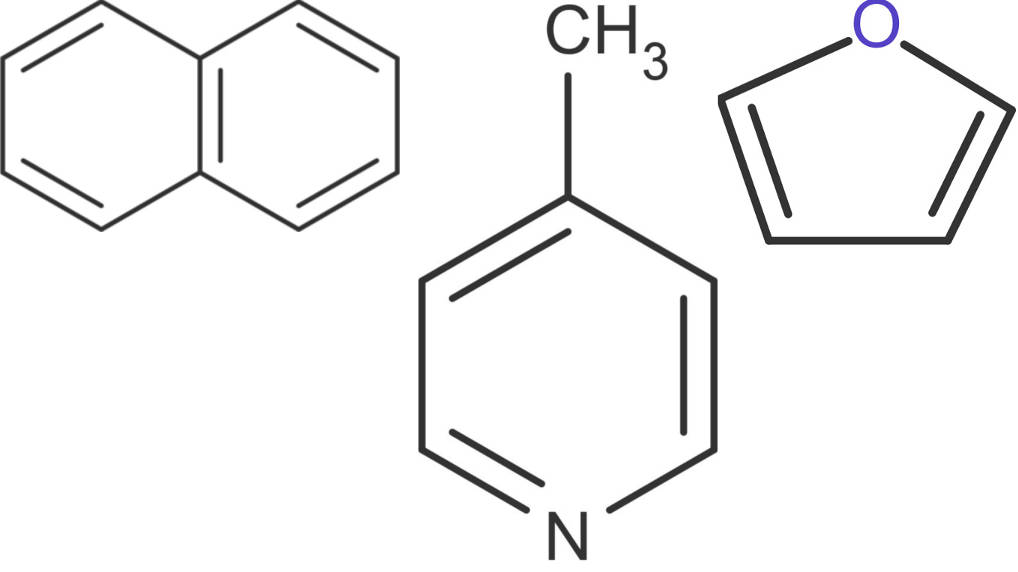
Naphtalin enthält zwei Ringe mit insgesamt fünf konjugierten Doppelbindungen. Ein Ring und zwei Doppelbindungen mehr ergibt das Anthracen. Es ist auch, möglich ein C-Atom des Rings gegen ein Stickstoffatom auszutauschen. Dann erhält man die Verbindung Pyridin. Diese kann ebenfalls substituiert (z.B. mit einer Methyl-Gruppe) vorliegen. Zu den delokalisierten Elektronen zählen auch freie Elektronen von Bindungspartnern. Daher zählt auch die Verbindung Furan zu den Aromaten.
Alle Videos zum Thema
Videos zum Thema
Aromatizität (4 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Aromatizität (2 Arbeitsblätter)
Beliebteste Themen in Chemie
- Periodensystem
- Ammoniak Verwendung
- Entropie
- Salzsäure Steckbrief
- Kupfer
- Stickstoff
- Glucose Und Fructose
- Salpetersäure
- Redoxreaktion
- Schwefelsäure
- Natronlauge
- Graphit
- Legierungen
- Dipol
- Molare Masse, Stoffmenge
- Sauerstoff
- Elektrolyse
- Bor
- Alkane
- Chlor
- Elektronegativität
- Tenside
- Toluol, Toluol Herstellung
- Wasserstoffbrückenbindung
- Fraktionierte Destillation Von Erdöl
- Carbonsäure
- Ester
- Harnstoff, Kohlensäure
- Reaktionsgleichung Aufstellen
- Cellulose Und Stärke Chemie
- Süßwasser Und Salzwasser
- Katalysator
- Ether
- Primärer Alkohol, Sekundärer Alkohol, Tertiärer Alkohol
- Van-der-Waals-Kräfte
- Oktettregel
- Kohlenstoffdioxid, Kohlenstoffmonoxid, Oxide
- Alfred Nobel Und Die Dynamit Entdeckung
- Wassermolekül
- Ionenbindung
- Phosphor
- Saccharose Und Maltose
- Kohlenwasserstoff
- Kovalente Bindungen
- Wasserhärte
- Peptidbindung
- Fermentation
- Nernst-Gleichung, Konzentrationsabhängigkeit Des Elektrodenpotentials
- Ethanol Als Lösungsmittel
- Kohlenstoff









 Aromaten
Aromaten
 Hückelregel
Hückelregel









