Grundlagen zur Energie
Der Satz von Hess, Lösungsenthalpie, Entropie, Berechnungsbeispiele, Gibbs-Helmholtz-Gleichung
Beliebteste Videos
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
Gleichgewichtslage bei chemischen Reaktionen
Die Thermodynamik beschäftigt sich mit der Änderung der Energiezustände der Moleküle während einer Reaktion. Dabei werden immer Gleichgewichtsreaktionen betrachtet.
Die Lage des Gleichgewichtes bei einer chemischen Reaktion lässt sich mit dem Massenwirkungsgesetz bestimmen. Im Gleichgewicht stellt sich eine Konstante zwischen der Konzentration der Edukte und der Konzentration der Produkte ein. Wird also die Konzentration der Edukte verändert, dann verändert sich automatisch die Konzentration der Produkte – solange, bis das passende Verhältnis des Gleichgewichtes wieder erreicht ist.

Für jede Reaktion lassen sich diese Konstanten bestimmen. Sie geben dir Auskunft, auf welcher Seite das Gleichgewicht liegt. Ist K sehr groß, dann ist die Konzentration an Produkten viel größer als die Konzentration an Edukten. Das Gleichgewicht liegt also stark auf Seiten der Produkte. Ist K dagegen sehr klein, dann liegt das Gleichgewicht stark auf Seiten der Edukte.
Die Lage des Gleichgewichtes lässt sich allerdings auch beeinflussen. Das Prinzip von le Chatelier sagt aus, dass Reaktionen äußeren Zwängen ausweichen. Die Lage eines Gleichgewichtes lässt sich dabei beeinflussen durch:
- Druck
- Temperatur
- Konzentration
Erhöht man also bei einer Reaktion, bei der mehr Gasmoleküle entstehen, als eingesetzt wurden, den Druck, dann weicht die Reaktion dem äußeren Zwang so aus, dass sich das Gleichgewicht auf Seiten der Edukte verschiebt, weil hier weniger Gasmoleküle vorhanden sind.
Die freie Enthalpie
Ob eine Reaktion freiwillig abläuft, gibt dir die freie Enthalpie der Reaktion an. Trägt sie ein negatives Vorzeichen, dann läuft die Reaktion ab, trägt sie ein positives Vorzeichen, dann läuft die Reaktion nicht freiwillig ab. Diese freie Energie setzt sich aus verschiedenen Größen zusammen, die du in der Gibbs-Helmholtz-Gleichung findest.
![]()
Zum einen besteht sie aus der Reaktionsenthalpie. Zusätzlich geht aber auch noch das Produkt aus Temperatur und der Entropie in die Gleichung ein. Die Entropie ist dabei ein Maß für die Unordnung. Je größer die Entropie, desto größer die Unordnung im Molekül. Moleküle streben dabei einen Zustand in größtmöglicher Unordnung an.
Bestimmung von Reaktionsenthalpien
Die Reaktionsenthalpie entspricht bei konstantem Druck der Reaktionswärme. Experimentell lässt sich daher die Reaktionsenthalpie mit einem Kalorimeter bestimmen. In einem Kalorimeter werden dabei Reaktionen durchgeführt und durch die Wärmeabgabe bei der Reaktion an das umgebende Wasser lässt sich die Reaktionsenthalpie bestimmen.
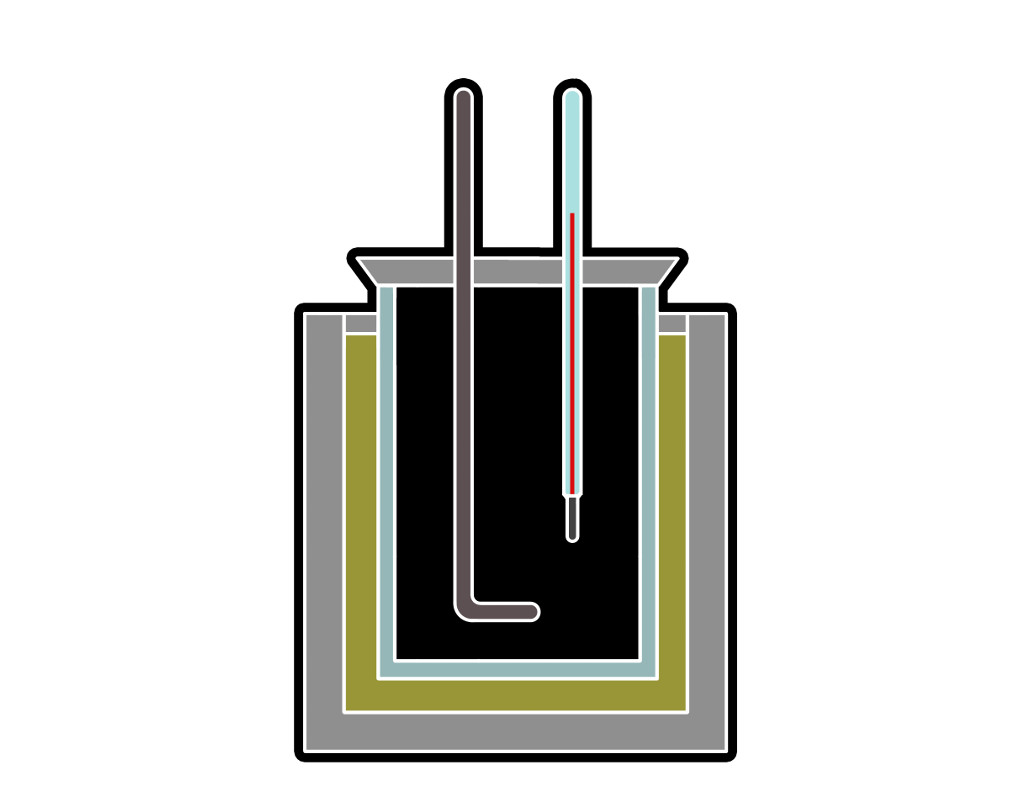
Es gibt allerdings auch einige Reaktionen, bei denen sich die Reaktionsenthalpie nicht experimentell bestimmen lässt. Dafür lässt sich der Satz von Hess verwenden. Dieser sagt aus, dass die Reaktionsenthalpie unabhängig vom Reaktionsweg ist und nur vom Ausgangs- und Endzustand des Systems abhängt.
Wenn zum Beispiel die Bildungsenthalpie von Kohlenstoffmonoxid bestimmt werden soll, dann kann dies nicht experimentell geschehen, da bei der Verbrennung von Kohlenstoff unmittelbar Kohlenstoffdioxid entstehen würde.
Die Enthalpie bei der Verbrennung von Kohlenstoff zu Kohlenstoffdioxid lässt sich experimentell bestimmen. Diese beträgt ΔH1 = -394 kJ/mol. Auch die Enthalpie der Verbrennung von Kohlenstoffmonoxid zu Kohlenstoffdioxid lässt sich bestimmen. Sie beträgt ΔH2 = -283 kJ/mol.

Diese Reaktionen lassen sich nun ins Verhältnis setzen, um die gesuchte Bildungsenthalpie von Kohlenstoffmonoxid (ΔH3) zu berechnen. ΔH1 - ΔH2 = ΔH3 = -111 kJ/mol.
Alle Videos zum Thema
Videos zum Thema
Grundlagen zur Energie (15 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Grundlagen zur Energie (10 Arbeitsblätter)
-
 Thermodynamik – Einführung
PDF anzeigen
Thermodynamik – Einführung
PDF anzeigen -
 Chemisches Gleichgewicht
PDF anzeigen
Chemisches Gleichgewicht
PDF anzeigen -
 Gleichgewichtsreaktionen – das Prinzip von Le Chatelier
PDF anzeigen
Gleichgewichtsreaktionen – das Prinzip von Le Chatelier
PDF anzeigen -
 Massenwirkungsgesetz – Überblick
PDF anzeigen
Massenwirkungsgesetz – Überblick
PDF anzeigen -
 Formulierung von Gleichgewichtsgleichungen (Übungsvideo)
PDF anzeigen
Formulierung von Gleichgewichtsgleichungen (Übungsvideo)
PDF anzeigen -
 Satz von Hess – Einführung
PDF anzeigen
Satz von Hess – Einführung
PDF anzeigen -
 Satz von Hess – Berechnung der Reaktionsenthalpie
PDF anzeigen
Satz von Hess – Berechnung der Reaktionsenthalpie
PDF anzeigen -
 Donnan-Gleichgewicht
PDF anzeigen
Donnan-Gleichgewicht
PDF anzeigen -
 Henry-Dalton-Gesetz
PDF anzeigen
Henry-Dalton-Gesetz
PDF anzeigen -
 Aktivierungsenergie
PDF anzeigen
Aktivierungsenergie
PDF anzeigen
Beliebteste Themen in Chemie
- Periodensystem
- Ammoniak Verwendung
- Entropie
- Salzsäure Steckbrief
- Kupfer
- Stickstoff
- Glucose Und Fructose
- Salpetersäure
- Redoxreaktion
- Schwefelsäure
- Natronlauge
- Graphit
- Legierungen
- Dipol
- Molare Masse, Stoffmenge
- Sauerstoff
- Elektrolyse
- Bor
- Alkane
- Chlor
- Elektronegativität
- Tenside
- Toluol, Toluol Herstellung
- Wasserstoffbrückenbindung
- Fraktionierte Destillation Von Erdöl
- Carbonsäure
- Ester
- Harnstoff, Kohlensäure
- Reaktionsgleichung Aufstellen
- Cellulose Und Stärke Chemie
- Süßwasser Und Salzwasser
- Katalysator
- Ether
- Primärer Alkohol, Sekundärer Alkohol, Tertiärer Alkohol
- Van-der-Waals-Kräfte
- Oktettregel
- Kohlenstoffdioxid, Kohlenstoffmonoxid, Oxide
- Alfred Nobel Und Die Dynamit Entdeckung
- Wassermolekül
- Ionenbindung
- Phosphor
- Saccharose Und Maltose
- Kohlenwasserstoff
- Kovalente Bindungen
- Wasserhärte
- Peptidbindung
- Fermentation
- Nernst-Gleichung, Konzentrationsabhängigkeit Des Elektrodenpotentials
- Ethanol Als Lösungsmittel
- Kohlenstoff




























